Modèles de classification dans la bibliothèque Scikit-Learn et leur export vers ONNX
MetaTrader 5
—
Exemples
| 26 août 2024, 10:31
531
0
Le développement de la technologie a conduit à l'émergence d'une approche fondamentalement nouvelle de la construction d'algorithmes de traitement des données. Avant cela, la résolution de chaque tâche spécifique nécessitait une formalisation claire et le développement d'algorithmes correspondants.
Avec l'apprentissage automatique, ou machine learning, l'ordinateur apprend à trouver les meilleurs moyens de traiter les données par lui-même. Les modèles d'apprentissage automatique peuvent résoudre avec succès des tâches de classification (lorsqu'il existe un ensemble fixe de classes et que l'objectif est de déterminer les probabilités d'appartenance à chaque classe d'un ensemble donné de caractéristiques) et des tâches de régression (lorsque l'objectif est d'estimer une valeur numérique de la variable cible sur la base d'un ensemble donné de caractéristiques). Des modèles de traitement de données plus complexes peuvent être élaborés à partir de ces composants fondamentaux.
La bibliothèque Scikit-learn fournit une multitude d'outils pour la classification et pour la régression. Le choix de méthodes et de modèles spécifiques dépend des caractéristiques des données, car différentes méthodes peuvent avoir une efficacité variable et fournir des résultats différents en fonction de la tâche.
Dans le communiqué de presse "ONNX Runtime is now open source", il est indiqué que le Runtime ONNX supporte également le profil ONNX-ML :
ONNX Runtime est le premier moteur d'inférence disponible publiquement avec un support complet pour ONNX 1.2 et supérieur, y compris le profil ONNX-ML.
Le profil ONNX-ML est une partie d'ONNX conçue spécifiquement pour les modèles d'apprentissage automatique (Machine Learning, ML). Il est destiné à décrire et à représenter divers types de modèles ML, tels que la classification, la régression, le regroupement et autres, dans un format pratique qui peut être utilisé sur diverses plateformes et environnements qui supportent ONNX. Le profil ONNX-ML simplifie la transmission, le déploiement et l'exécution des modèles d'apprentissage automatique, les rendant plus accessibles et portables.
Dans cet article, nous allons explorer l'application de tous les modèles de classification dans le paquet Scikit-learn pour résoudre la tâche de classification de l'Iris de Fisher. Nous tenterons également de convertir ces modèles au format ONNX et d'utiliser les modèles résultants dans les programmes MQL5.
Nous comparerons également la précision des modèles originaux avec leurs versions ONNX sur l'ensemble des données Iris.
Table des Matières
- 1. Iris de Fisher
- 2. Modèles de Classification
Liste des Classificateurs Scikit-learn
Différentes Représentations de Sortie des Modèles iris.mqh - 2.1. Classificateur SVC
2.1.1. Code de Création du Modèle de Classification SVC
2.1.2. Code MQL5 pour travailler avec le modèle de classification SVC
2.1.3. Représentation ONNX du modèle de classification SVC - 2.2. Classificateur LinearSVC
2.2.1. Code de création du modèle de classification LinearSVC
2.2.2. Code MQL5 pour travailler avec le modèle de classification LinearSVC
2.2.3. Représentation ONNX du modèle de classification LinearSVC - 2.3. NuSVC Classifier
2.3.1. Code de création du modèle de classification NuSVC
2.3.2. Code MQL5 pour travailler avec le modèle de classification NuSVC
2.3.3. Représentation ONNX du modèle de classification NuSVC - 2.4. Classificateur Radius Neighbors
2.4.1. Code de création du modèle de classification Radius Neighbors
2.4.2. Code MQL5 pour travailler avec le modèle de classification Radius Neighbors
2.3.3. Représentation ONNX du modèle de classification Radius Neighbors - 2.5. Classificateur Ridge
2.5.1. Code de création du modèle de classification Ridge
2.5.2. Code MQL5 pour travailler avec le modèle de classification Ridge
2.5.3. Représentation ONNX du modèle de classification Ridge - 2.6. RidgeClassifierCV
2.6.1. Code de création du modèle Ridge ClassifierCV
2.6.2. Code MQL5 pour travailler avec le modèle Ridge ClassifierCV
2.6.3. Représentation ONNX du modèle Ridge ClassifierCV - 2.7. Classificateur Random Forest
2.7.1. Code pour la création du modèle de classification Random Forest
2.7.2. Code MQL5 pour travailler avec le modèle de classification Random Forest
2.7.3. Représentation ONNX du modèle de classification Random Forest - 2.8. Classificateur Gradient Boosting
2.8.1. Code pour la création du Modèle de Classification Gradient Boosting
2.8.2. Code MQL5 pour Travailler avec le Modèle de Classification Gradient Boosting
2.8.3. Représentation ONNX du Modèle de Classification Gradient Boosting - 2.9. Classificateur Boosting Adaptative
2.9.1. Code pour la Création du Modèle de Classificateur Boosting Adaptative
2.9.2. Code MQL5 pour Travailler avec le Modèle de Classification Adaptive Boosting
2.9.3. Représentation ONNX du Modèle de Classification Adaptative Boosting - 2.10. Classificateur Bootstrap Aggregating
2.10.1. Code pour la Création du Modèle Bootstrap Aggregating Classifier
2.10.2. Code MQL5 pour Travailler avec le Modèle Bootstrap Aggregating Classifier
2.10.3. Représentation ONNX du Modèle de Classification Bootstrap Aggregating - 2.11. Classificateur K-Nearest Neighbors (K-NN)
2.11.1. Code pour la Création du Modèle de Classification K-NN (K-Nearest Neighbors)
2.11.2. Code MQL5 pour Travailler avec le Modèle de Classification K-NN (K-Nearest Neighbors)
2.11.3. Représentation ONNX du Modèle de Classification K-NN (K-NN) - 2.12. Classificateur Decision Tree (Arbre de Décision)
2.12.1. Code pour la Création du Modèle de Classification Decision Tree
2.12.2. Code MQL5 pour Travailler avec le Modèle de Classification Decision Tree
2.12.3. Représentation ONNX du Modèle de Classification Decision Tree - 2.13. Classificateur de Régression Logistique (Logistic Regression)
2.13.1. Code de Création du Modèle de Classification Logistic Regression
2.13.2. Code MQL5 pour Travailler avec le Modèle Logistic Regression
2.13.3. Représentation ONNX du Modèle de Classification Logistic Regression - 2.14. Classificateur LogisticRegressionCV
2.14.1. Code de Création du Modèle de Classification LogisticRegressionCV
2.14.2. Code MQL5 pour Travailler avec le Modèle de Classification LogisticRegressionCV
2.14.3. Représentation ONNX du Modèle de Classification LogisticRegressionCV - 2.15. Classificateur Passif-Agressif (PA)
2.15.1. Code pour la Création du Modèle de Classificateur Passif-Agressif (PA)
2.15.2. Code MQL5 pour Travailler avec le Modèle de Classificateur Passif-Agressif (PA)
2.15.3. Représentation ONNX du Modèle de Classificateur Passif-Agressif (PA) - 2.16. Classificateur Perceptron
2.16.1. Code de Création du Modèle de Classification Perceptron
2.16.2. Code MQL5 pour Travailler avec le Modèle de Classification Perceptron
2.16.3. Représentation ONNX du Modèle de Classification Perceptron - 2.17. Classificateur Stochastic Gradient Descent
2.17.1. Code de Création du Modèle de Classification Stochastic Gradient Descent
2.17.2. Code MQL5 pour Travailler avec le Modèle de Classification Stochastic Gradient Descent
2.17.3. Représentation ONNX du Modèle de Classification Stochastic Gradient Descent - 2.18. Classificateur Gaussian Naive Bayes (GNB)
2.18.1. Code de Création du Modèle de Classification Gaussian Naive Bayes (GNB)
2.18.2. Code MQL5 pour Travailler avec le Modèle de Classification Gaussian Naive Bayes (GNB)
2.18.3. Représentation ONNX du Modèle de Classification Gaussian Naive Bayes (GNB) - 2.19. Classificateur Multinomial Naive Bayes (MNB)
2.19.1. Code de Création du Modèle de Classification Multinomial Naive Bayes (MNB)
2.19.2. Code MQL5 pour Travailler avec le Modèle de Classification Multinomial Naive Bayes (MNB)
2.19.3. Représentation ONNX du Modèle de Classification Multinomial Naive Bayes (MNB) - 2.20. Classificateur Complement Naive Bayes (CNB)
2.20.1. Code pour la Création du Modèle de Classification Complement Naive Bayes (CNB)
2.20.2. Code MQL5 pour Travailler avec le Modèle de Classification Complement Naive Bayes (CNB)
2.20.3. Représentation ONNX du Modèle de Classification Complement Naive Bayes (CNB) - 2.21. Classificateur Bernoulli Naive Bayes (BNB)
2.21.1. Code de Création du Modèle de Classification Bernoulli Naive Bayes (BNB)
2.21.2. Code MQL5 pour Travailler avec le Modèle de Classification Bernoulli Naive Bayes (BNB)
2.21.3. Représentation ONNX du Modèle de Classification Bernoulli Naive Bayes (BNB) - 2.22. Multilayer Perceptron Classifier
2.22.1. Code pour la Création du Modèle de Classification Multilayer Perceptron
2.22.2. Code MQL5 pour Travailler avec le Modèle de Classification Multilayer Perceptron
2.22.3. Représentation ONNX du Modèle de Classification Multilayer Perceptron - 2.23. Classificateur Linear Discriminant Analysis (LDA)
2.23.1. Code de Création du Modèle de Classification Linear Discriminant Analysis (LDA)
2.23.2. Code MQL5 pour Travailler avec le Modèle de Classification Linear Discriminant Analysis (LDA)
2.23.3. Représentation ONNX du Modèle de Classification Linear Discriminant Analysis (LDA) - 2.24. Hist Gradient Boosting
2.24.1. Code pour la Création du Modèle de Classification Histogram-Based Gradient Boosting
2.24.2. Code MQL5 pour Travailler avec le Modèle de Classification Histogram-Based Gradient Boosting
2.24.3. Représentation ONNX du Modèle de Classification Histogram-Based Gradient Boosting - 2.25. Classificateur CategoricalNB
2.25.1. Code pour la Création du Modèle de Classification CategoricalNB
2.25.2. Code MQL5 pour Travailler avec le Modèle de Classification CategoricalNB
2.25.3. Représentation ONNX du Modèle de Classification CategoricalNB - 2.26. ExtraTreeClassifier
2.26.1. Code de Création du Modèle ExtraTreeClassifier
2.26.2. Code MQL5 pour Travailler avec le Modèle ExtraTreeClassifier
2.26.3. Représentation ONNX du Modèle ExtraTreeClassifier - 2.27. ExtraTreesClassifier
2.27.1. Code de Création du Modèle ExtraTreesClassifier
2.27.2. Code MQL5 pour Travailler avec le Modèle ExtraTreesClassifier
2.27.3. Représentation ONNX du Modèle ExtraTreesClassifier - 2.28. Comparaison de la Précision de Tous les Modèles
2.28.1. Code pour le Calcul de Tous les Modèles et Construire un Tableau de Comparaison de la Précision
2.28.2. Code MQL5 pour l'Exécution de Tous les Modèles ONNX - 2.29. Modèles de Classification Scikit-Learn qui n'ont pas pu être convertis en ONNX
- 2.29.1. DummyClassifier
2.29.1.1. Code de Création du Modèle DummyClassifier - 2.29.2. GaussianProcessClassifier
2.29.2.1. Code de Création du Modèle GaussianProcessClassifier - 2.29.3. Classificateur LabelPropagation
2.29.3.1. Code de Création du Modèle LabelPropagationClassifier - 2.29.4. Classificateur LabelSpreading
2.29.4.1. Code de Création du Modèle LabelSpreadingClassifier - 2.29.5. Classificateur NearestCentroid
2.29.5.1. Code pour la Création du Modèle NearestCentroid - 2.29.6. Classificateur Quadratic Discriminant Analysis
2.29.6.1. Code pour la Création du Modèle Quadratic Discriminant Analysis - Conclusions
1. Iris de Fisher
L'ensemble de données Iris est l'un des ensembles de données les plus connus et les plus utilisés dans le domaine de l'apprentissage automatique. Il a été introduit pour la première fois en 1936 par le statisticien et biologiste R.A. Fisher et est devenu depuis un ensemble de données classique pour les tâches de classification.
L'ensemble de données Iris consiste en des mesures de sépales et de pétales de trois espèces d'iris : Iris setosa, Iris virginica et Iris versicolor.
Figure 1. Iris setosa
Figure 2. Iris virginica
Figure 3. Iris versicolor
L'ensemble de données Iris comprend 150 instances d'iris, avec 50 instances de chacune des trois espèces. Chaque instance a 4 caractéristiques numériques (mesurées en centimètres) :
- Longueur du sépale
- Largeur du sépale
- Longueur du pétale
- Largeur du pétale
Chaque instance a également une classe correspondante indiquant l'espèce d'iris (Iris setosa, Iris virginica ou Iris versicolor). Cette caractéristique de classification fait de l'ensemble de données Iris un ensemble de données idéal pour les tâches d'apprentissage automatique telles que la classification et le regroupement.
MetaEditor permet de travailler avec des scripts Python. Pour créer un script Python, sélectionnez "Nouveau" dans le menu "Fichier" de MetaEditor, et une boîte de dialogue permettant de choisir l'objet à créer apparaît (voir figure 4).
Figure 4. Création d'un script Python dans l'Assistant MQL5 - Etape 1
Donnez ensuite un nom au script, par exemple "IRIS.py" (voir figure 5).
Figure 5. Création d'un script Python dans l'Assistant MQL5 - Etape 2 - Nom du script
Vous pouvez ensuite spécifier les bibliothèques qui seront utilisées. Dans notre cas, nous laisserons ces champs vides (voir figure 6).
Figure 6 : Création d'un script Python dans l'Assistant MQL5 - Etape 3
L'une des façons de commencer l'analyse de l'ensemble de données Iris est de visualiser les données. Une représentation graphique nous permet de mieux comprendre la structure des données et les relations entre les caractéristiques.
Par exemple, vous pouvez créer un diagramme de dispersion pour voir comment les différentes espèces d'iris sont réparties dans l'espace des caractéristiques.
Code du script Python :
# The script shows the scatter plot of the Iris dataset features # Copyright 2023, MetaQuotes Ltd. # https://mql5.com import matplotlib.pyplot as plt from sklearn import datasets # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # extract sepal length and sepal width (the first two features) sepal_length = X[:, 0] sepal_width = X[:, 1] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(sepal_length, sepal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Sepal Length (cm)') plt.ylabel('Sepal Width (cm)') plt.title('Scatter Plot for Sepal Length and Sepal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_sepal_length_width.png') # Extract petal length and petal width (the third and fourth features) petal_length = X[:, 2] petal_width = X[:, 3] # create a scatter plot plt.figure(figsize=(8, 6)) plt.scatter(petal_length, petal_width, c=y, cmap=plt.cm.Set1, edgecolor='k') plt.xlabel('Petal Length (cm)') plt.ylabel('Petal Width (cm)') plt.title('Scatter Plot for Petal Length and Petal Width') plt.colorbar(label='Iris Species', ticks=[0, 1, 2]) plt.show() # save the scatter plot to a file (optional) # plt.savefig('scatter_plot_petal_length_width.png')
Pour exécuter ce script, vous devez le copier dans MetaEditor (voir figure 7) et cliquer sur "Compiler".
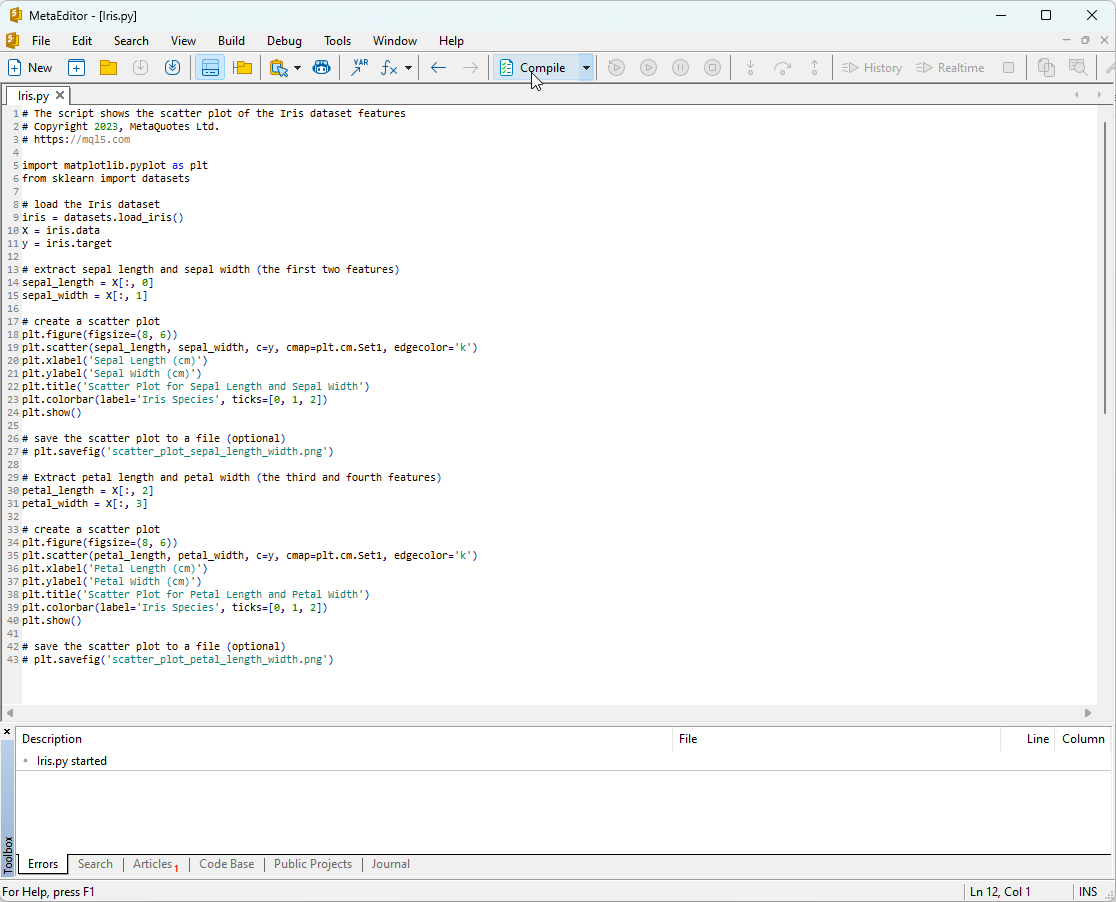
Figure 7 : Script IRIS.py dans MetaEditor
Ensuite, les parcelles s'affichent à l'écran :
Figure 8 : Le script IRIS.py dans MetaEditor avec le tracé de la longueur et de la largeur des sépales
Figure 9 : Le script IRIS.py dans MetaEditor avec le tracé de la longueur et de la largeur des pétales
Examinons-les de plus près.
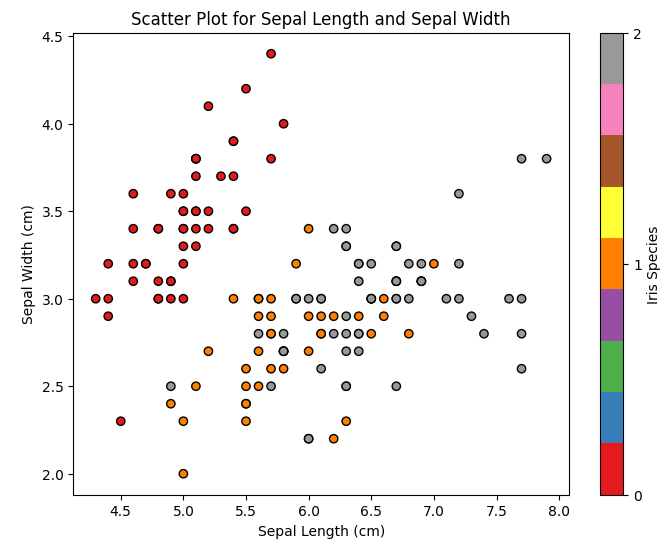
Figure 10 : Diagramme de dispersion de la longueur du sépale vs la largeur du sépale
Ce graphique montre la répartition des différentes espèces d'iris en fonction de la longueur et de la largeur des sépales. Nous pouvons observer que l'Iris setosa a typiquement des sépales plus courts et plus larges que les deux autres espèces.
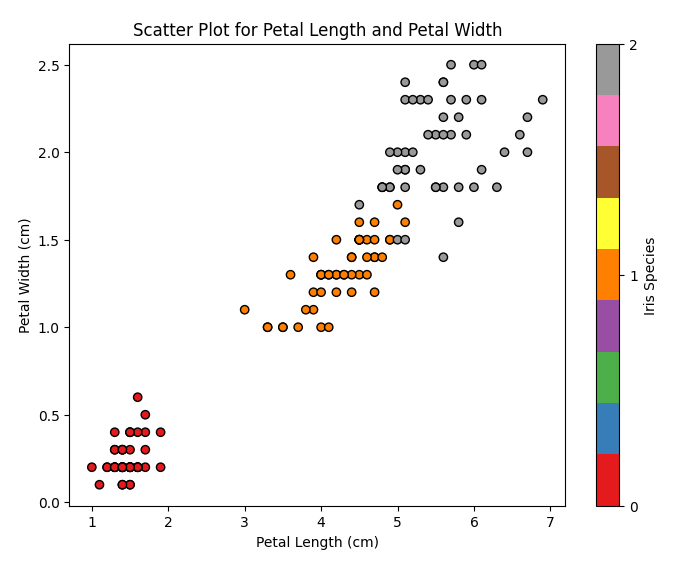
Figure 11 : Diagramme de dispersion de la longueur du pétale par rapport à la largeur du pétale
Ce graphique montre la répartition des différentes espèces d'iris en fonction de la longueur et de la largeur des pétales. Nous pouvons remarquer que l'Iris setosa a les pétales les plus courts et les plus étroits, l'Iris virginica a les pétales les plus longs et les plus larges, et l'Iris versicolor se situe entre les deux.
L'ensemble de données Iris est un ensemble de données idéal pour former et tester des modèles d'apprentissage automatique. Nous l'utiliserons pour analyser l'efficacité des modèles d'apprentissage automatique pour une tâche de classification.
2. Modèles de Classification
La classification est l'une des tâches fondamentales de l'apprentissage automatique. Son objectif est de classer les données dans différentes catégories, ou classes, sur la base de certaines caractéristiques.
Explorons les principaux modèles d'apprentissage automatique du paquet scikit-learn.
Liste des Classificateurs Scikit-learn
Pour afficher la liste des classificateurs disponibles dans scikit-learn, vous pouvez utiliser le script suivant :
# ScikitLearnClassifiers.py # The script lists all the classification algorithms available in scikit-learn # Copyright 2023, MetaQuotes Ltd. # https://mql5.com # print Python version from platform import python_version print("The Python version is ", python_version()) # print scikit-learn version import sklearn print('The scikit-learn version is {}.'.format(sklearn.__version__)) # print scikit-learn classifiers from sklearn.utils import all_estimators classifiers = all_estimators(type_filter='classifier') for index, (name, ClassifierClass) in enumerate(classifiers, start=1): print(f"Classifier {index}: {name}")
Sortie :
Python The Python version is 3.10.0
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Python The scikit-learn version is 1.2.2.
Python Classifier 1: AdaBoostClassifier
Python Classifier 2: BaggingClassifier
Python Classifier 3: BernoulliNB
Python Classifier 4: CalibratedClassifierCV
Python Classifier 5: CategoricalNB
Python Classifier 6: ClassifierChain
Python Classifier 7: ComplementNB
Python Classifier 8: DecisionTreeClassifier
Python Classifier 9: DummyClassifier
Python Classifier 10: ExtraTreeClassifier
Python Classifier 11: ExtraTreesClassifier
Python Classifier 12: GaussianNB
Python Classifier 13: GaussianProcessClassifier
Python Classifier 14: GradientBoostingClassifier
Python Classifier 15: HistGradientBoostingClassifier
Python Classifier 16: KNeighborsClassifier
Python Classifier 17: LabelPropagation
Python Classifier 18: LabelSpreading
Python Classifier 19: LinearDiscriminantAnalysis
Python Classifier 20: LinearSVC
Python Classifier 21: LogisticRegression
Python Classifier 22: LogisticRegressionCV
Python Classifier 23: MLPClassifier
Python Classifier 24: MultiOutputClassifier
Python Classifier 25: MultinomialNB
Python Classifier 26: NearestCentroid
Python Classifier 27: NuSVC
Python Classifier 28: OneVsOneClassifier
Python Classifier 29: OneVsRestClassifier
Python Classifier 30: OutputCodeClassifier
Python Classifier 31: PassiveAggressiveClassifier
Python Classifier 32: Perceptron
Python Classifier 33: QuadraticDiscriminantAnalysis
Python Classifier 34: RadiusNeighborsClassifier
Python Classifier 35: RandomForestClassifier
Python Classifier 36: RidgeClassifier
Python Classifier 37: RidgeClassifierCV
Python Classifier 38: SGDClassifier
Python Classifier 39: SVC
Python Classifier 40: StackingClassifier
Python Classifier 41: VotingClassifier
Pour plus de visibilité dans cette liste de classificateurs, ils sont mis en évidence par des couleurs différentes. Les modèles qui nécessitent des classificateurs de base sont surlignés en jaune, les autres modèles peuvent être utilisés indépendamment.
Pour l'avenir, il est intéressant de noter que les modèles colorés en vert ont été exportés avec succès au format ONNX. Les modèles colorés en rouge rencontrent des erreurs lors de la conversion dans la version actuelle de scikit-learn 1.2.2.
Différentes représentations des données de sortie dans les modèles
Il convient de noter que les différents modèles représentent les données de sortie différemment. Il faut donc être attentif lorsque l'on travaille avec des modèles convertis en ONNX.
Pour la tâche de classification de l'Iris de Fisher, les tenseurs d'entrée ont le même format pour tous ces modèles :
Informations sur les tenseurs d'entrée dans ONNX :
1. Nom : float_input, Type de Données : tensor(float), Forme : [None, 4]
1. Nom : float_input, Type de Données : tensor(float), Forme : [None, 4]
Les tenseurs de sortie des modèles ONNX sont différents.
1. Modèles ne nécessitant pas de post-traitement :
- Classificateur SVC
- Classificateur LinearSVC
- NuSVC Classifier
- Classificateur Radius Neighbors
- Classificateur Ridge
- Classificateur Ridge CV
Informations sur les tenseurs de sortie dans ONNX :
1. Nom : label, Type de Données : tensor(int64), Forme : [None]
2. Name : probabilities, Type de Données : tensor(float), Forme : [None, 3]
1. Nom : label, Type de Données : tensor(int64), Forme : [None]
2. Name : probabilities, Type de Données : tensor(float), Forme : [None, 3]
Ces modèles renvoient le résultat (numéro de classe) explicitement dans le premier tenseur entier de sortie "label", sans nécessiter de post-traitement.
2. Modèles dont les résultats nécessitent un post-traitement :
- Classification Random Forest
- Classificateur Gradient Boosting
- Classificateur AdaBoost
- Classificateur Bagging
- Classificateur K-NN
- Classificateur Decision Tree
- Classificateur Logistic Regression
- Classificateur Logistic Regression CV
- Classificateur Passif-Agressif
- Classificateur Perceptron
- Classificateur SGD
- Classificateur Gaussian Naive Bayes
- Classificateur Multinomial Naive Bayes
- Classificateur Complement Naive Bayes
- Classificateur Bernoulli Naive Bayes
- Classification Multilayer Perceptron
- Classificateur Linear Discriminant Analysis
- Classificateur Hist Gradient Boosting
- Classificateur Categorical Naive Bayes
- Classificateur ExtraTree
- Classificateur ExtraTrees
Informations sur les tenseurs de sortie dans ONNX :
1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
2. Nom : output_probability, Type de Données : seq(map(int64,tensor(float))), Forme : []
1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
2. Nom : output_probability, Type de Données : seq(map(int64,tensor(float))), Forme : []
Ces modèles renvoient une liste de classes et de probabilités d'appartenance à chaque classe.
Pour obtenir le résultat dans ces cas, un post-traitement est nécessaire, tel que seq(map(int64, tensor(float)) (recherche de l'élément ayant la probabilité la plus élevée).
Il est donc essentiel d'être attentif et de prendre en compte ces aspects lorsque l'on travaille avec des modèles ONNX. Un exemple de traitement différent des résultats est présenté dans le script au point 2.28.2.
iris.mqh
Pour tester les modèles sur l'ensemble des données Iris dans MQL5, une préparation des données est nécessaire. Pour cela, la fonction PrepareIrisDataset() sera utilisée.
Il est pratique de déplacer ces fonctions dans le fichier iris.mqh.
//+------------------------------------------------------------------+ //| Iris.mqh | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" //+------------------------------------------------------------------+ //| Structure for the IRIS Dataset sample | //+------------------------------------------------------------------+ struct sIRISsample { int sample_id; // sample id (1-150) double features[4]; // SepalLengthCm,SepalWidthCm,PetalLengthCm,PetalWidthCm string class_name; // class ("Iris-setosa","Iris-versicolor","Iris-virginica") int class_id; // class id (0,1,2), calculated by function IRISClassID }; //--- Iris dataset sIRISsample ExtIRISDataset[]; int Exttotal=0; //+------------------------------------------------------------------+ //| Returns class id by class name | //+------------------------------------------------------------------+ int IRISClassID(string class_name) { //--- if(class_name=="Iris-setosa") return(0); else if(class_name=="Iris-versicolor") return(1); else if(class_name=="Iris-virginica") return(2); //--- return(-1); } //+------------------------------------------------------------------+ //| AddSample | //+------------------------------------------------------------------+ bool AddSample(const int Id,const double SepalLengthCm,const double SepalWidthCm,const double PetalLengthCm,const double PetalWidthCm, const string Species) { //--- ExtIRISDataset[Exttotal].sample_id=Id; //--- ExtIRISDataset[Exttotal].features[0]=SepalLengthCm; ExtIRISDataset[Exttotal].features[1]=SepalWidthCm; ExtIRISDataset[Exttotal].features[2]=PetalLengthCm; ExtIRISDataset[Exttotal].features[3]=PetalWidthCm; //--- ExtIRISDataset[Exttotal].class_name=Species; ExtIRISDataset[Exttotal].class_id=IRISClassID(Species); //--- Exttotal++; //--- return(true); } //+------------------------------------------------------------------+ //| Prepare Iris Dataset | //+------------------------------------------------------------------+ bool PrepareIrisDataset(sIRISsample &iris_samples[]) { ArrayResize(ExtIRISDataset,150); Exttotal=0; //--- AddSample(1,5.1,3.5,1.4,0.2,"Iris-setosa"); AddSample(2,4.9,3.0,1.4,0.2,"Iris-setosa"); AddSample(3,4.7,3.2,1.3,0.2,"Iris-setosa"); AddSample(4,4.6,3.1,1.5,0.2,"Iris-setosa"); AddSample(5,5.0,3.6,1.4,0.2,"Iris-setosa"); AddSample(6,5.4,3.9,1.7,0.4,"Iris-setosa"); AddSample(7,4.6,3.4,1.4,0.3,"Iris-setosa"); AddSample(8,5.0,3.4,1.5,0.2,"Iris-setosa"); AddSample(9,4.4,2.9,1.4,0.2,"Iris-setosa"); AddSample(10,4.9,3.1,1.5,0.1,"Iris-setosa"); AddSample(11,5.4,3.7,1.5,0.2,"Iris-setosa"); AddSample(12,4.8,3.4,1.6,0.2,"Iris-setosa"); AddSample(13,4.8,3.0,1.4,0.1,"Iris-setosa"); AddSample(14,4.3,3.0,1.1,0.1,"Iris-setosa"); AddSample(15,5.8,4.0,1.2,0.2,"Iris-setosa"); AddSample(16,5.7,4.4,1.5,0.4,"Iris-setosa"); AddSample(17,5.4,3.9,1.3,0.4,"Iris-setosa"); AddSample(18,5.1,3.5,1.4,0.3,"Iris-setosa"); AddSample(19,5.7,3.8,1.7,0.3,"Iris-setosa"); AddSample(20,5.1,3.8,1.5,0.3,"Iris-setosa"); AddSample(21,5.4,3.4,1.7,0.2,"Iris-setosa"); AddSample(22,5.1,3.7,1.5,0.4,"Iris-setosa"); AddSample(23,4.6,3.6,1.0,0.2,"Iris-setosa"); AddSample(24,5.1,3.3,1.7,0.5,"Iris-setosa"); AddSample(25,4.8,3.4,1.9,0.2,"Iris-setosa"); AddSample(26,5.0,3.0,1.6,0.2,"Iris-setosa"); AddSample(27,5.0,3.4,1.6,0.4,"Iris-setosa"); AddSample(28,5.2,3.5,1.5,0.2,"Iris-setosa"); AddSample(29,5.2,3.4,1.4,0.2,"Iris-setosa"); AddSample(30,4.7,3.2,1.6,0.2,"Iris-setosa"); AddSample(31,4.8,3.1,1.6,0.2,"Iris-setosa"); AddSample(32,5.4,3.4,1.5,0.4,"Iris-setosa"); AddSample(33,5.2,4.1,1.5,0.1,"Iris-setosa"); AddSample(34,5.5,4.2,1.4,0.2,"Iris-setosa"); AddSample(35,4.9,3.1,1.5,0.2,"Iris-setosa"); AddSample(36,5.0,3.2,1.2,0.2,"Iris-setosa"); AddSample(37,5.5,3.5,1.3,0.2,"Iris-setosa"); AddSample(38,4.9,3.6,1.4,0.1,"Iris-setosa"); AddSample(39,4.4,3.0,1.3,0.2,"Iris-setosa"); AddSample(40,5.1,3.4,1.5,0.2,"Iris-setosa"); AddSample(41,5.0,3.5,1.3,0.3,"Iris-setosa"); AddSample(42,4.5,2.3,1.3,0.3,"Iris-setosa"); AddSample(43,4.4,3.2,1.3,0.2,"Iris-setosa"); AddSample(44,5.0,3.5,1.6,0.6,"Iris-setosa"); AddSample(45,5.1,3.8,1.9,0.4,"Iris-setosa"); AddSample(46,4.8,3.0,1.4,0.3,"Iris-setosa"); AddSample(47,5.1,3.8,1.6,0.2,"Iris-setosa"); AddSample(48,4.6,3.2,1.4,0.2,"Iris-setosa"); AddSample(49,5.3,3.7,1.5,0.2,"Iris-setosa"); AddSample(50,5.0,3.3,1.4,0.2,"Iris-setosa"); AddSample(51,7.0,3.2,4.7,1.4,"Iris-versicolor"); AddSample(52,6.4,3.2,4.5,1.5,"Iris-versicolor"); AddSample(53,6.9,3.1,4.9,1.5,"Iris-versicolor"); AddSample(54,5.5,2.3,4.0,1.3,"Iris-versicolor"); AddSample(55,6.5,2.8,4.6,1.5,"Iris-versicolor"); AddSample(56,5.7,2.8,4.5,1.3,"Iris-versicolor"); AddSample(57,6.3,3.3,4.7,1.6,"Iris-versicolor"); AddSample(58,4.9,2.4,3.3,1.0,"Iris-versicolor"); AddSample(59,6.6,2.9,4.6,1.3,"Iris-versicolor"); AddSample(60,5.2,2.7,3.9,1.4,"Iris-versicolor"); AddSample(61,5.0,2.0,3.5,1.0,"Iris-versicolor"); AddSample(62,5.9,3.0,4.2,1.5,"Iris-versicolor"); AddSample(63,6.0,2.2,4.0,1.0,"Iris-versicolor"); AddSample(64,6.1,2.9,4.7,1.4,"Iris-versicolor"); AddSample(65,5.6,2.9,3.6,1.3,"Iris-versicolor"); AddSample(66,6.7,3.1,4.4,1.4,"Iris-versicolor"); AddSample(67,5.6,3.0,4.5,1.5,"Iris-versicolor"); AddSample(68,5.8,2.7,4.1,1.0,"Iris-versicolor"); AddSample(69,6.2,2.2,4.5,1.5,"Iris-versicolor"); AddSample(70,5.6,2.5,3.9,1.1,"Iris-versicolor"); AddSample(71,5.9,3.2,4.8,1.8,"Iris-versicolor"); AddSample(72,6.1,2.8,4.0,1.3,"Iris-versicolor"); AddSample(73,6.3,2.5,4.9,1.5,"Iris-versicolor"); AddSample(74,6.1,2.8,4.7,1.2,"Iris-versicolor"); AddSample(75,6.4,2.9,4.3,1.3,"Iris-versicolor"); AddSample(76,6.6,3.0,4.4,1.4,"Iris-versicolor"); AddSample(77,6.8,2.8,4.8,1.4,"Iris-versicolor"); AddSample(78,6.7,3.0,5.0,1.7,"Iris-versicolor"); AddSample(79,6.0,2.9,4.5,1.5,"Iris-versicolor"); AddSample(80,5.7,2.6,3.5,1.0,"Iris-versicolor"); AddSample(81,5.5,2.4,3.8,1.1,"Iris-versicolor"); AddSample(82,5.5,2.4,3.7,1.0,"Iris-versicolor"); AddSample(83,5.8,2.7,3.9,1.2,"Iris-versicolor"); AddSample(84,6.0,2.7,5.1,1.6,"Iris-versicolor"); AddSample(85,5.4,3.0,4.5,1.5,"Iris-versicolor"); AddSample(86,6.0,3.4,4.5,1.6,"Iris-versicolor"); AddSample(87,6.7,3.1,4.7,1.5,"Iris-versicolor"); AddSample(88,6.3,2.3,4.4,1.3,"Iris-versicolor"); AddSample(89,5.6,3.0,4.1,1.3,"Iris-versicolor"); AddSample(90,5.5,2.5,4.0,1.3,"Iris-versicolor"); AddSample(91,5.5,2.6,4.4,1.2,"Iris-versicolor"); AddSample(92,6.1,3.0,4.6,1.4,"Iris-versicolor"); AddSample(93,5.8,2.6,4.0,1.2,"Iris-versicolor"); AddSample(94,5.0,2.3,3.3,1.0,"Iris-versicolor"); AddSample(95,5.6,2.7,4.2,1.3,"Iris-versicolor"); AddSample(96,5.7,3.0,4.2,1.2,"Iris-versicolor"); AddSample(97,5.7,2.9,4.2,1.3,"Iris-versicolor"); AddSample(98,6.2,2.9,4.3,1.3,"Iris-versicolor"); AddSample(99,5.1,2.5,3.0,1.1,"Iris-versicolor"); AddSample(100,5.7,2.8,4.1,1.3,"Iris-versicolor"); AddSample(101,6.3,3.3,6.0,2.5,"Iris-virginica"); AddSample(102,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(103,7.1,3.0,5.9,2.1,"Iris-virginica"); AddSample(104,6.3,2.9,5.6,1.8,"Iris-virginica"); AddSample(105,6.5,3.0,5.8,2.2,"Iris-virginica"); AddSample(106,7.6,3.0,6.6,2.1,"Iris-virginica"); AddSample(107,4.9,2.5,4.5,1.7,"Iris-virginica"); AddSample(108,7.3,2.9,6.3,1.8,"Iris-virginica"); AddSample(109,6.7,2.5,5.8,1.8,"Iris-virginica"); AddSample(110,7.2,3.6,6.1,2.5,"Iris-virginica"); AddSample(111,6.5,3.2,5.1,2.0,"Iris-virginica"); AddSample(112,6.4,2.7,5.3,1.9,"Iris-virginica"); AddSample(113,6.8,3.0,5.5,2.1,"Iris-virginica"); AddSample(114,5.7,2.5,5.0,2.0,"Iris-virginica"); AddSample(115,5.8,2.8,5.1,2.4,"Iris-virginica"); AddSample(116,6.4,3.2,5.3,2.3,"Iris-virginica"); AddSample(117,6.5,3.0,5.5,1.8,"Iris-virginica"); AddSample(118,7.7,3.8,6.7,2.2,"Iris-virginica"); AddSample(119,7.7,2.6,6.9,2.3,"Iris-virginica"); AddSample(120,6.0,2.2,5.0,1.5,"Iris-virginica"); AddSample(121,6.9,3.2,5.7,2.3,"Iris-virginica"); AddSample(122,5.6,2.8,4.9,2.0,"Iris-virginica"); AddSample(123,7.7,2.8,6.7,2.0,"Iris-virginica"); AddSample(124,6.3,2.7,4.9,1.8,"Iris-virginica"); AddSample(125,6.7,3.3,5.7,2.1,"Iris-virginica"); AddSample(126,7.2,3.2,6.0,1.8,"Iris-virginica"); AddSample(127,6.2,2.8,4.8,1.8,"Iris-virginica"); AddSample(128,6.1,3.0,4.9,1.8,"Iris-virginica"); AddSample(129,6.4,2.8,5.6,2.1,"Iris-virginica"); AddSample(130,7.2,3.0,5.8,1.6,"Iris-virginica"); AddSample(131,7.4,2.8,6.1,1.9,"Iris-virginica"); AddSample(132,7.9,3.8,6.4,2.0,"Iris-virginica"); AddSample(133,6.4,2.8,5.6,2.2,"Iris-virginica"); AddSample(134,6.3,2.8,5.1,1.5,"Iris-virginica"); AddSample(135,6.1,2.6,5.6,1.4,"Iris-virginica"); AddSample(136,7.7,3.0,6.1,2.3,"Iris-virginica"); AddSample(137,6.3,3.4,5.6,2.4,"Iris-virginica"); AddSample(138,6.4,3.1,5.5,1.8,"Iris-virginica"); AddSample(139,6.0,3.0,4.8,1.8,"Iris-virginica"); AddSample(140,6.9,3.1,5.4,2.1,"Iris-virginica"); AddSample(141,6.7,3.1,5.6,2.4,"Iris-virginica"); AddSample(142,6.9,3.1,5.1,2.3,"Iris-virginica"); AddSample(143,5.8,2.7,5.1,1.9,"Iris-virginica"); AddSample(144,6.8,3.2,5.9,2.3,"Iris-virginica"); AddSample(145,6.7,3.3,5.7,2.5,"Iris-virginica"); AddSample(146,6.7,3.0,5.2,2.3,"Iris-virginica"); AddSample(147,6.3,2.5,5.0,1.9,"Iris-virginica"); AddSample(148,6.5,3.0,5.2,2.0,"Iris-virginica"); AddSample(149,6.2,3.4,5.4,2.3,"Iris-virginica"); AddSample(150,5.9,3.0,5.1,1.8,"Iris-virginica"); //--- ArrayResize(iris_samples,150); for(int i=0; i<Exttotal; i++) { iris_samples[i]=ExtIRISDataset[i]; } //--- return(true); } //+------------------------------------------------------------------+
Note sur les méthodes de classification : SVC, LinearSVC et NuSVC
Comparons 3 méthodes de classification courantes : SVC (Support Vector Classification), LinearSVC (Linear Support Vector Classification) et NuSVC (Nu Support Vector Classification).
Principes de Fonctionnement :
SVC (Support Vector Classification)
Principe de Fonctionnement : Le SVC est une méthode de classification basée sur la maximisation de la marge entre les classes. Il recherche un hyperplan de séparation optimal qui sépare au maximum les classes et soutient les vecteurs de soutien - les points les plus proches de l'hyperplan.
Fonctions Noyau : Le SVC peut utiliser différentes fonctions noyau, telles que la fonction linéaire, la fonction de base radiale (RBF), la fonction polynomiale et d'autres encore. La fonction noyau détermine comment les données sont transformées pour trouver l'hyperplan optimal.
LinearSVC (Linear Support Vector Classification)
Principe de Fonctionnement : LinearSVC est une variante de SVC spécialisée dans la classification linéaire. Elle recherche un hyperplan de séparation linéaire optimal sans utiliser de fonctions noyau. Elle est donc plus rapide et plus efficace lorsqu'il s'agit de travailler avec de grands volumes de données.
NuSVC (Nu Support Vector Classification)
Principe de Fonctionnement : NuSVC est également basé sur les méthodes de vecteurs de support mais introduit un paramètre Nu (nu), qui contrôle la complexité du modèle et la fraction des vecteurs de support. La valeur Nu est comprise entre 0 et 1 et détermine la part des données qui peut être utilisée pour les vecteurs de support et pour les erreurs.
Avantages :
SVC
Algorithme Puissant : Le SVC peut gérer des tâches de classification complexes et travailler avec des données non linéaires grâce à l'utilisation de fonctions noyau.
Robustesse face aux valeurs aberrantes : Le SVC est résistant aux données aberrantes car il utilise des vecteurs de support pour construire l'hyperplan de séparation.
LinearSVC
Haute Efficacité : LinearSVC est plus rapide et plus efficace lorsqu'il s'agit de traiter de grands ensembles de données, en particulier lorsque les données sont volumineuses et que la séparation linéaire est adaptée à la tâche.
Classification Linéaire : Si le problème est bien linéairement séparable, LinearSVC peut donner de bons résultats sans qu'il soit nécessaire d'utiliser des fonctions noyau complexes.
NuSVC
Contrôle de la Complexité des Modèles : Le paramètre Nu de NuSVC vous permet de contrôler la complexité du modèle et le compromis entre l'adaptation aux données et la généralisation.
Robustesse face aux valeurs aberrantes : Comme le SVC, le NuSVC est résistant aux valeurs aberrantes, ce qui le rend utile pour les tâches impliquant des données bruyantes.
Limites :
SVC
Complexité de Calcul : Le SVC peut être lent sur de grands ensembles de données et/ou lors de l'utilisation de fonctions de noyau complexes.
Sensibilité du Noyau : Le choix de la bonne fonction noyau peut être une tâche difficile et avoir un impact significatif sur la performance du modèle.
LinearSVC
Contrainte de Linéarité : LinearSVC est limité par la séparation linéaire des données et peut donner de mauvais résultats dans les cas de dépendances non linéaires entre les caractéristiques et la variable cible.
NuSVC
Réglage du Paramètre Nu : Le réglage du paramètre Nu peut nécessiter du temps et des tests pour obtenir des résultats optimaux.
En fonction des caractéristiques de la tâche et du volume de données, chacune de ces méthodes peut constituer le meilleur choix. Il est important de mener des expériences et de sélectionner la méthode qui répond le mieux aux exigences spécifiques de la tâche de classification.
Comparons 3 méthodes de classification courantes : SVC (Support Vector Classification), LinearSVC (Linear Support Vector Classification) et NuSVC (Nu Support Vector Classification).
Principes de Fonctionnement :
SVC (Support Vector Classification)
Principe de Fonctionnement : Le SVC est une méthode de classification basée sur la maximisation de la marge entre les classes. Il recherche un hyperplan de séparation optimal qui sépare au maximum les classes et soutient les vecteurs de soutien - les points les plus proches de l'hyperplan.
Fonctions Noyau : Le SVC peut utiliser différentes fonctions noyau, telles que la fonction linéaire, la fonction de base radiale (RBF), la fonction polynomiale et d'autres encore. La fonction noyau détermine comment les données sont transformées pour trouver l'hyperplan optimal.
LinearSVC (Linear Support Vector Classification)
Principe de Fonctionnement : LinearSVC est une variante de SVC spécialisée dans la classification linéaire. Elle recherche un hyperplan de séparation linéaire optimal sans utiliser de fonctions noyau. Elle est donc plus rapide et plus efficace lorsqu'il s'agit de travailler avec de grands volumes de données.
NuSVC (Nu Support Vector Classification)
Principe de Fonctionnement : NuSVC est également basé sur les méthodes de vecteurs de support mais introduit un paramètre Nu (nu), qui contrôle la complexité du modèle et la fraction des vecteurs de support. La valeur Nu est comprise entre 0 et 1 et détermine la part des données qui peut être utilisée pour les vecteurs de support et pour les erreurs.
Avantages :
SVC
Algorithme Puissant : Le SVC peut gérer des tâches de classification complexes et travailler avec des données non linéaires grâce à l'utilisation de fonctions noyau.
Robustesse face aux valeurs aberrantes : Le SVC est résistant aux données aberrantes car il utilise des vecteurs de support pour construire l'hyperplan de séparation.
LinearSVC
Haute Efficacité : LinearSVC est plus rapide et plus efficace lorsqu'il s'agit de traiter de grands ensembles de données, en particulier lorsque les données sont volumineuses et que la séparation linéaire est adaptée à la tâche.
Classification Linéaire : Si le problème est bien linéairement séparable, LinearSVC peut donner de bons résultats sans qu'il soit nécessaire d'utiliser des fonctions noyau complexes.
NuSVC
Contrôle de la Complexité des Modèles : Le paramètre Nu de NuSVC vous permet de contrôler la complexité du modèle et le compromis entre l'adaptation aux données et la généralisation.
Robustesse face aux valeurs aberrantes : Comme le SVC, le NuSVC est résistant aux valeurs aberrantes, ce qui le rend utile pour les tâches impliquant des données bruyantes.
Limites :
SVC
Complexité de Calcul : Le SVC peut être lent sur de grands ensembles de données et/ou lors de l'utilisation de fonctions de noyau complexes.
Sensibilité du Noyau : Le choix de la bonne fonction noyau peut être une tâche difficile et avoir un impact significatif sur la performance du modèle.
LinearSVC
Contrainte de Linéarité : LinearSVC est limité par la séparation linéaire des données et peut donner de mauvais résultats dans les cas de dépendances non linéaires entre les caractéristiques et la variable cible.
NuSVC
Réglage du Paramètre Nu : Le réglage du paramètre Nu peut nécessiter du temps et des tests pour obtenir des résultats optimaux.
En fonction des caractéristiques de la tâche et du volume de données, chacune de ces méthodes peut constituer le meilleur choix. Il est important de mener des expériences et de sélectionner la méthode qui répond le mieux aux exigences spécifiques de la tâche de classification.
2.1. Classificateur SVC
La méthode de classification Support Vector Classification (SVC) est un puissant algorithme d'apprentissage automatique largement utilisé pour résoudre les tâches de classification.
Principes de Fonctionnement :
- Hyper-plan de Séparation Optimal
Principe de Fonctionnement : L'idée principale du SVC est de trouver l'hyper-plan de séparation optimal dans l'espace des caractéristiques. Cet hyper-plan doit maximiser la séparation entre les objets de différentes classes et soutenir les vecteurs de soutien, qui sont les points de données les plus proches de l'hyper-plan.
Maximiser la Marge : Le SVC vise à maximiser la marge entre les classes, c'est-à-dire la distance entre les vecteurs de support et l'hyper-plan. Cela permet à la méthode d'être résistante aux valeurs aberrantes et de bien s'adapter à de nouvelles données. - Utilisation des Fonctions Noyau
Fonctions Noyau : Le SVC peut utiliser différentes fonctions noyau, telles que la fonction linéaire, la fonction de base radiale (RBF), la fonction polynomiale et d'autres encore. La fonction noyau permet de projeter les données dans un espace de dimension supérieure où la tâche devient linéaire, même s'il n'y a pas de séparabilité linéaire dans l'espace de données d'origine.
Sélection du Noyau : Le choix de la bonne fonction noyau peut avoir un impact significatif sur les performances du modèle SVC. Un hyper-plan linéaire n'est pas toujours la solution optimale.
Avantages :
- Algorithme Puissant. Gérer des Tâches Complexes : Le SVC peut résoudre des tâches de classification complexes, y compris celles qui présentent des dépendances non linéaires entre les caractéristiques et la variable cible.
- Robustesse face aux valeurs aberrantes : L'utilisation de vecteurs de support rend la méthode robuste aux données aberrantes. Elle dépend des vecteurs de support plutôt que de l'ensemble des données.
- Flexibilité du Noyau. Adaptabilité aux Données : La possibilité d'utiliser différentes fonctions noyau permet à SVC de s'adapter à des données spécifiques et de découvrir des relations non linéaires.
- Bonne Généralisation. Généralisation à de Nouvelles Données : Le modèle SVC peut se généraliser à de nouvelles données, ce qui le rend utile pour les tâches de prédiction.
Limites :
- Complexité de Calcul. Durée de la Formation : L'apprentissage du SVC peut être lent, en particulier lorsqu'il s'agit de grands volumes de données ou de fonctions noyau complexes.
- Sélection du Noyau. Choisir la Bonne Fonction Noyau : La sélection de la bonne fonction noyau peut nécessiter des tests et dépend des caractéristiques des données.
- Sensibilité à la Mise à l'Echelle des Caractéristiques. Normalisation des Données : Le SVC est sensible à la mise à l'échelle des caractéristiques, il est donc recommandé de normaliser ou de standardiser les données avant l'entraînement.
- Interprétabilité du Modèle. Complexité d'Interprétation : Les modèles SVC peuvent être complexes à interpréter en raison de l'utilisation de noyaux non linéaires et d'une multitude de vecteurs de support.
En fonction de la tâche spécifique et du volume de données, la méthode SVC peut être un outil puissant pour résoudre les tâches de classification. Mais il est essentiel de tenir compte de ses limites et de régler les paramètres pour obtenir des résultats optimaux.
2.1.1. Code de Création du Modèle de Classification SVC
Ce code démontre le processus d'entraînement d'un modèle de Classificateur SVC sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_SVCClassifier.py # The code demonstrates the process of training SVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import SVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SVC Classifier model with a linear kernel svc_model = SVC(kernel='linear', C=1.0) # train the model on the entire dataset svc_model.fit(X, y) # predict classes for the entire dataset y_pred = svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SVC Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SVC Classifier model in ONNX format:", accuracy_onnx)
Après avoir exécuté le script dans MetaEditor en utilisant le bouton "Compiler", vous pouvez voir les résultats de son exécution dans l'onglet Journal.
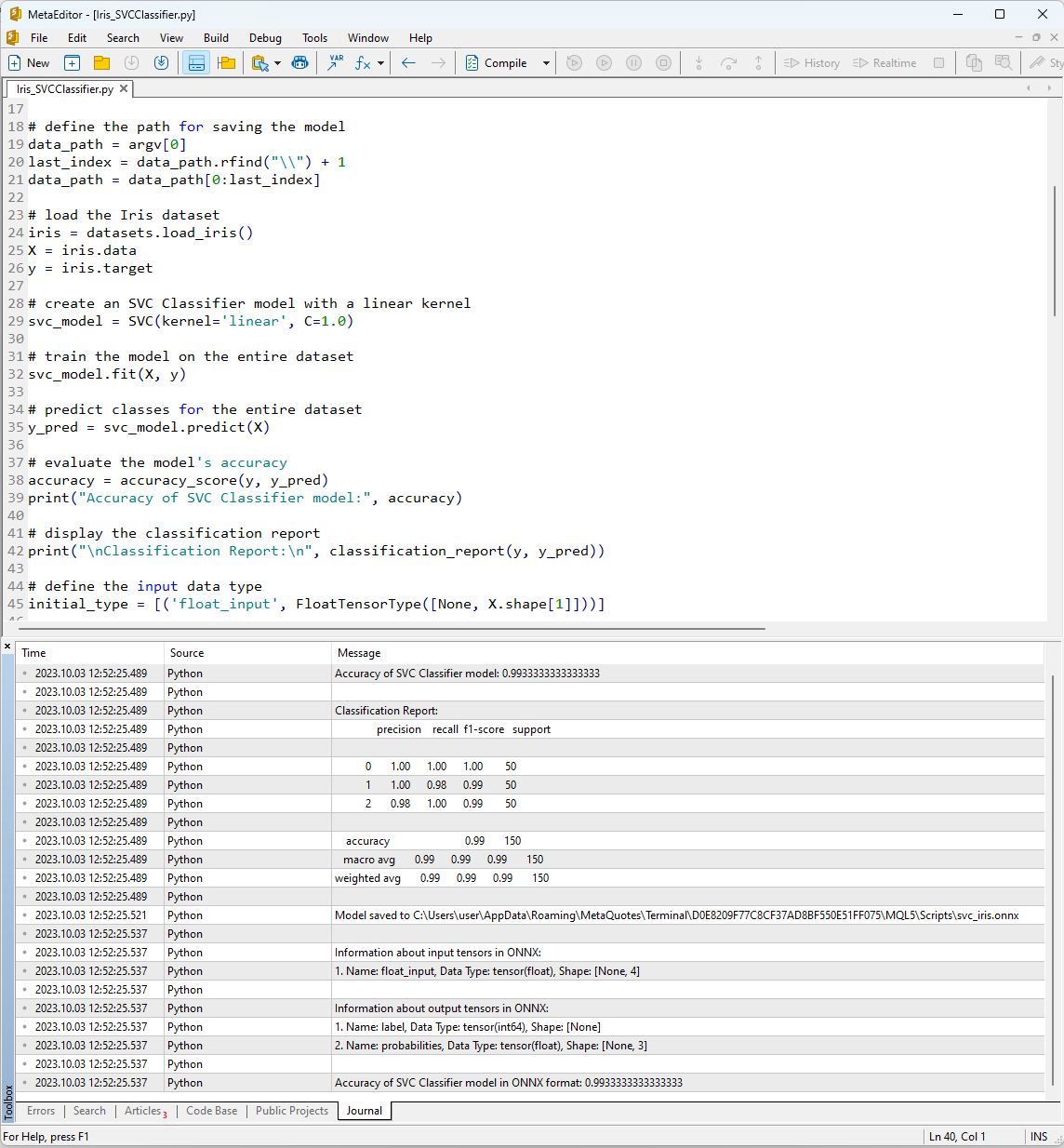
Figure 12. Résultats du script Iris_SVMClassifier.py dans MetaEditor
Sortie du script Iris_SVCClassifier.py :
Python Accuracy of SVC Classifier model: 0.9933333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.98 0.99 50
Python 2 0.98 1.00 0.99 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of SVC Classifier model in ONNX format: 0.9933333333333333
Vous trouverez ici des informations sur le chemin où le modèle ONNX a été sauvegardé, les types de paramètres d'entrée et de sortie du modèle ONNX, ainsi que la précision dans la description de l'ensemble de données Iris.
La précision de la description de l'ensemble de données à l'aide du Classificateur SVM est de 99 %, et le modèle exporté au format ONNX présente le même niveau de précision.
Nous allons maintenant vérifier ces résultats dans MQL5 en exécutant le modèle construit pour chacun des 150 échantillons de données. Le script comprend également un exemple de traitement des données par lots.
2.1.2. Code MQL5 pour travailler avec le modèle de Classification SVC
//+------------------------------------------------------------------+ //| Iris_SVCClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SVCClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Les résultats de l'exécution du script sont affichés dans l'onglet "Experts" du terminal MetaTrader 5.
Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SVCClassifier (EURUSD,H1) model:SVCClassifier correct results: 99.33% Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier all samples accuracy=0.993333 Iris_SVCClassifier (EURUSD,H1) model=SVCClassifier batch test accuracy=1.000000
Le modèle SVC a correctement classé 149 échantillons sur 150, ce qui est un excellent résultat. Le modèle n'a commis qu'une seule erreur de classification dans l'ensemble de données Iris, en prédisant la classe 2 (versicolor) au lieu de la classe 1 (virginica) pour l'échantillon n° 84.
Il est intéressant de noter que la précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 99,33 %, ce qui correspond à la précision du modèle original.
2.1.3. Représentation ONNX du Modèle de Classification SVC
Vous pouvez visualiser le modèle ONNX construit dans MetaEditor.
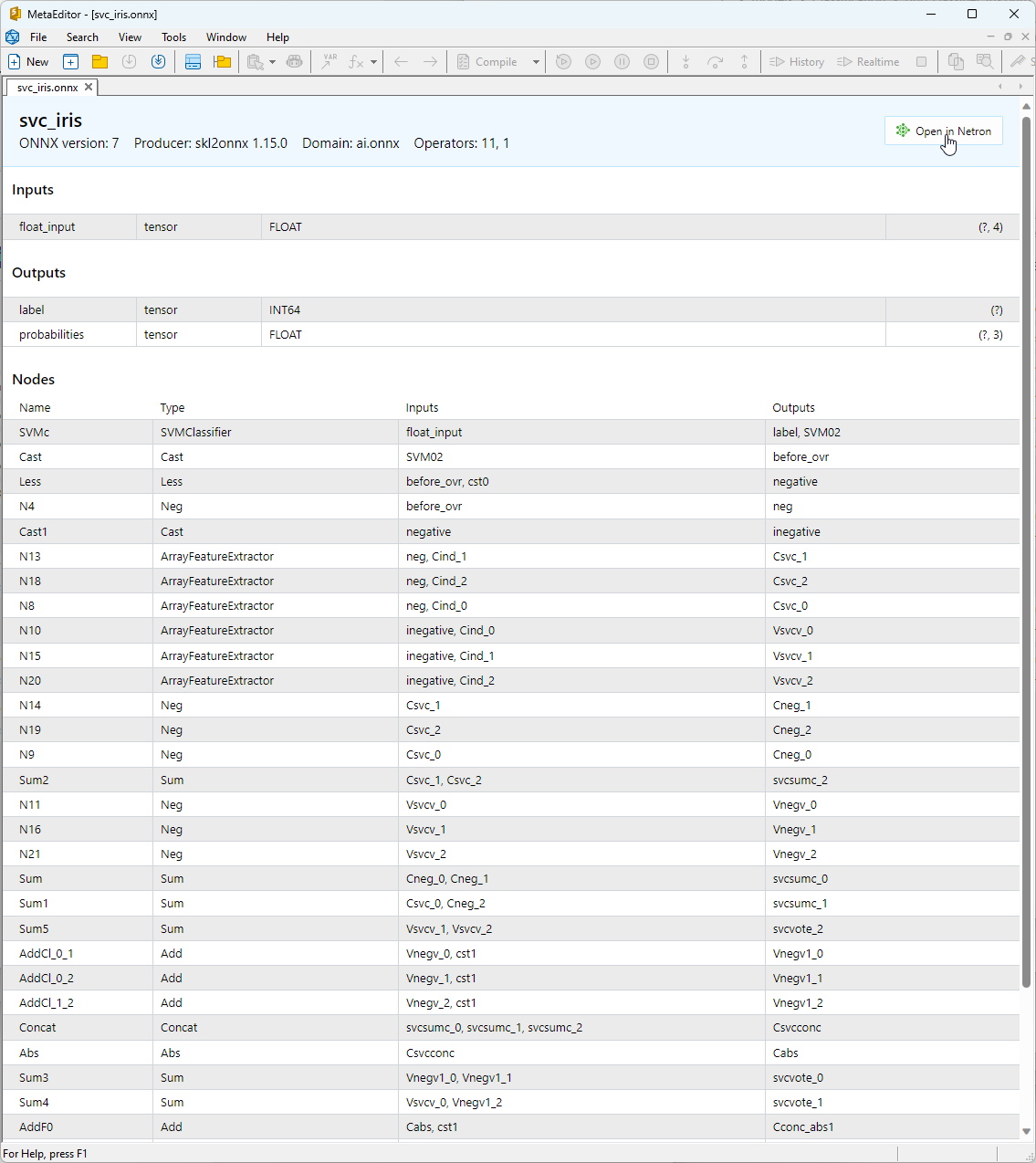
Figure 13. Modèle ONNX svc_iris.onnx dans MetaEditor
Pour obtenir des informations plus détaillées sur l'architecture du modèle, vous pouvez utiliser Netron. Pour cela, cliquez sur le bouton "Ouvrir dans Netron" dans la description du modèle dans MetaEditor.
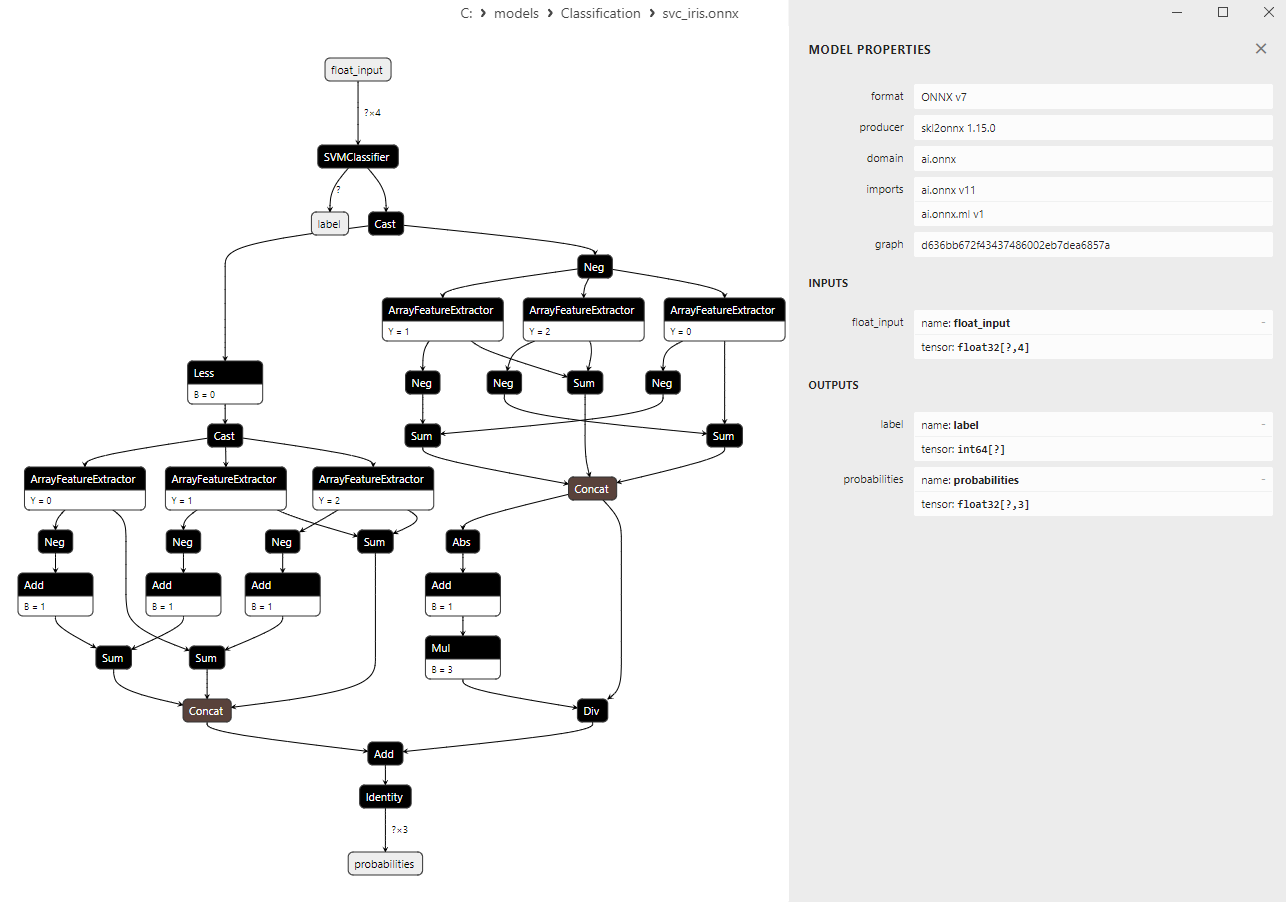
Figure 14. Modèle ONNX svc_iris.onnx dans Netron
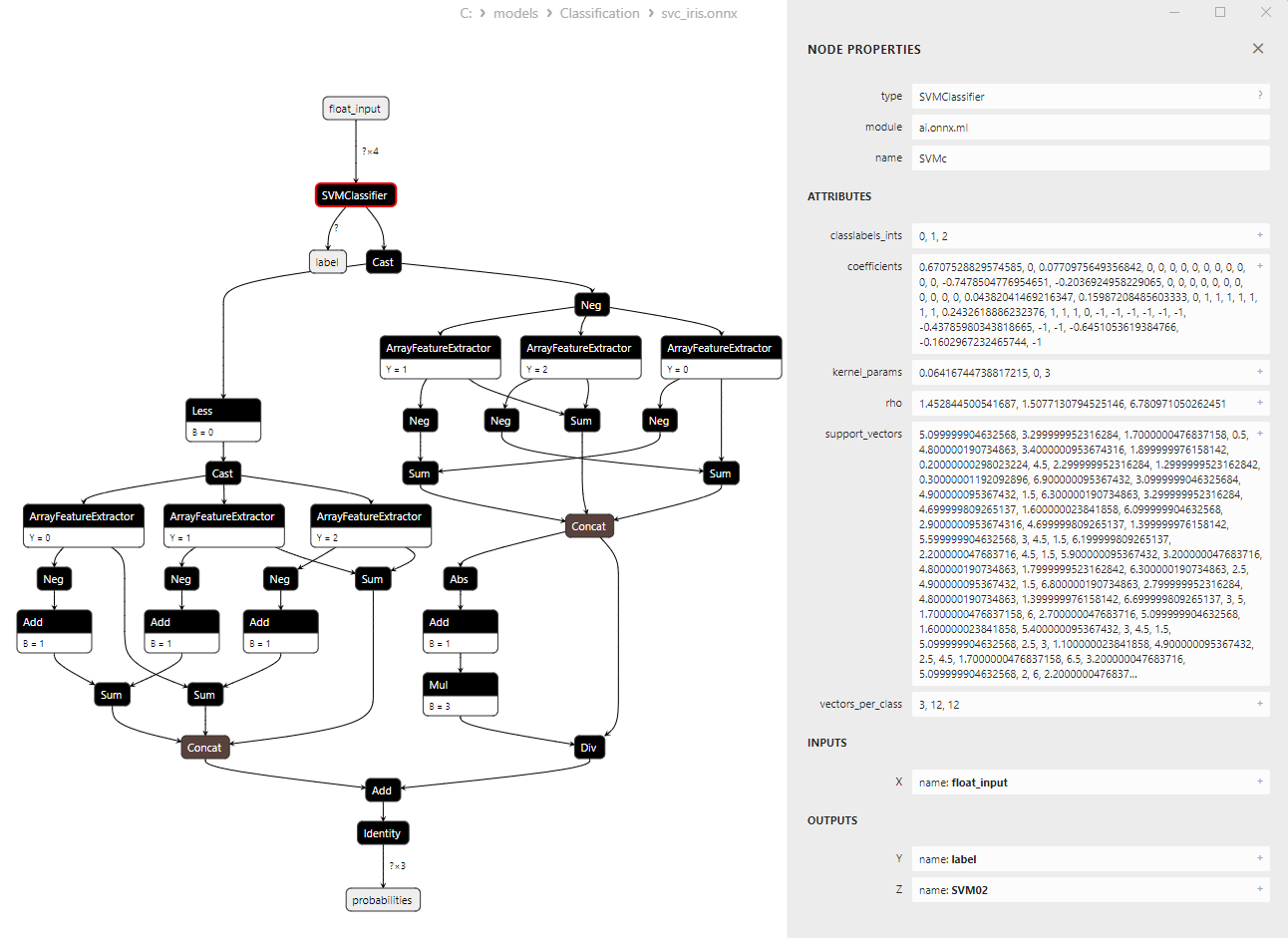
Figure 15. Modèle ONNX svc_iris.onnx dans Netron (SVMClassifier ONNX Operator Parameters)
2.2. Classificateur LinearSVC
LinearSVC (Linear Support Vector Classification) est un puissant algorithme d'apprentissage automatique utilisé pour les tâches de classification binaire et multi-classe. Il est basé sur l'idée de trouver un hyper-plan qui sépare au mieux les données.
Principes de LinearSVC :
- Recherche de l'hyper-plan optimal : L'idée principale de LinearSVC est de trouver l'hyper-plan optimal qui sépare au maximum les deux classes de données. Un hyper-plan est un plan multidimensionnel défini par une équation linéaire.
- Minimisation de la Marge : LinearSVC vise à minimiser les marges (les distances entre les points de données et l'hyper-plan). Plus les marges sont importantes, plus l'hyper-plan sépare efficacement les classes.
- Traitement de données linéairement non séparables : LinearSVC peut travailler avec des données qui ne peuvent pas être séparées linéairement dans l'espace des caractéristiques d'origine, grâce à l'utilisation de fonctions noyau (kernel trick) qui projettent les données dans un espace de dimension supérieure où elles peuvent être séparées linéairement.
Avantages de LinearSVC :
- Bonne Généralisation : LinearSVC a une bonne capacité de généralisation et peut donner de bons résultats sur de nouvelles données inédites.
- Efficacité : LinearSVC fonctionne rapidement sur de grands ensembles de données et nécessite relativement peu de ressources de calcul.
- Traitement de données linéairement non séparables : En utilisant des fonctions noyau, LinearSVC peut traiter des tâches de classification avec des données linéairement non séparables.
- Évolutivité : LinearSVC peut être utilisé efficacement dans les tâches comportant un grand nombre de caractéristiques et des volumes de données importants.
Limites de LinearSVC :
- Uniquement des hyper-plans de séparation linéaires : LinearSVC ne construit que des hyper-plans de séparation linéaires, ce qui peut s'avérer insuffisant pour les tâches de classification complexes comportant des dépendances non linéaires.
- Sélection des Paramètres : Le choix des bons paramètres (par exemple, le paramètre de régularisation) peut nécessiter des connaissances d'expert ou une validation croisée.
- Sensibilité aux valeurs aberrantes : LinearSVC peut être sensible aux valeurs aberrantes dans les données, ce qui peut affecter la qualité de la classification.
- Interprétabilité du modèle : Les modèles créés à l'aide de LinearSVC peuvent être moins faciles à interpréter que d'autres méthodes.
LinearSVC est un algorithme de classification puissant qui excelle dans la généralisation, l'efficacité et le traitement de données linéairement non séparables. Il trouve des applications dans diverses tâches de classification, en particulier lorsque les données peuvent être séparées par un hyper-plan linéaire. Mais pour les tâches complexes qui nécessitent la modélisation de dépendances non linéaires, LinearSVC peut s'avérer moins adapté. Dans ce cas, il convient d'envisager d'autres méthodes avec des limites de décision plus complexes.
2.2.1. Code pour la Création du Modèle de Classification LinearSVC
Ce code démontre le processus d'entraînement d'un modèle de classification LinearSVC sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_LinearSVC.py # The code demonstrates the process of training LinearSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import LinearSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LinearSVC model linear_svc_model = LinearSVC(C=1.0, max_iter=10000) # train the model on the entire dataset linear_svc_model.fit(X, y) # predict classes for the entire dataset y_pred = linear_svc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LinearSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(linear_svc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "linear_svc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LinearSVC model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of LinearSVC model: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.94 0.95 50
Python 2 0.94 0.96 0.95 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\linear_svc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of LinearSVC model in ONNX format: 0.9666666666666667
2.2.2. Code MQL5 pour Travailler avec le Modèle de Classification LinearSVC
//+------------------------------------------------------------------+ //| Iris_LinearSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "linear_svc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LinearSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_LinearSVC (EURUSD,H1) model:LinearSVC sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LinearSVC (EURUSD,H1) model:LinearSVC correct results: 96.67% Iris_LinearSVC (EURUSD,H1) model=LinearSVC all samples accuracy=0.966667 Iris_LinearSVC (EURUSD,H1) model=LinearSVC batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 96,67 %, ce qui correspond à la précision du modèle original.
2.2.3. Représentation ONNX du Modèle de Classification LinearSVC
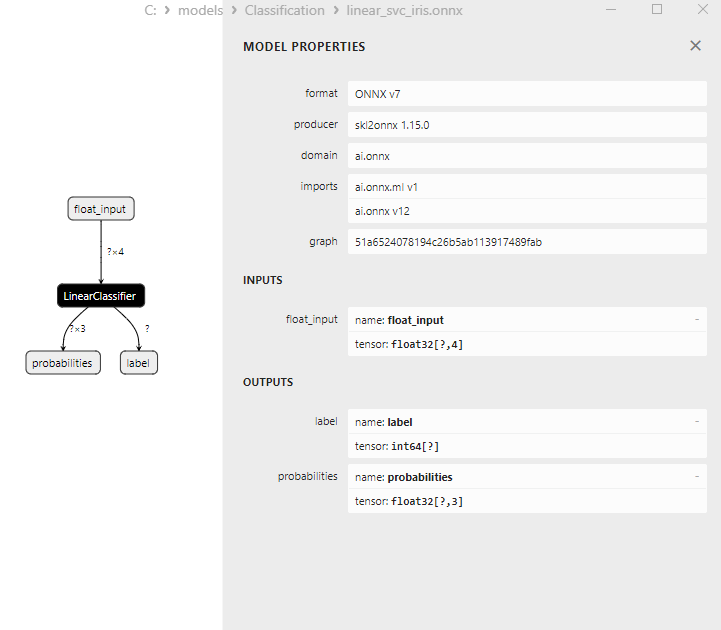
Figure 16. Représentation ONNX du Modèle de Classification LinearSVC dans Netron
2.3. Classificateur NuSVC
La méthode Nu-Support Vector Classification (NuSVC) est un puissant algorithme d'apprentissage automatique basé sur l'approche Support Vector Machine (SVM).
Principes de NuSVC :
- Support Vector Machine (SVM) : NuSVC est une variante des SVM utilisée pour les tâches de classification binaire et multi-classe. Le principe de base des SVM est de trouver l'hyper-plan de séparation optimal qui sépare au maximum les classes tout en conservant une marge maximale.
- Le Paramètre Nu : Un paramètre clé de NuSVC est le paramètre Nu (nu), qui contrôle la complexité du modèle et définit la proportion de l'échantillon qui peut être utilisée comme vecteurs de support et d'erreurs. La valeur de Nu est comprise entre 0 et 1, où 0,5 signifiant qu'environ la moitié de l'échantillon sera utilisée comme vecteurs de support et d'erreurs.
- Réglage des Paramètres : La détermination des valeurs optimales du paramètre Nu et d'autres hyper-paramètres peut nécessiter une validation croisée et une recherche des meilleures valeurs sur les données d'apprentissage.
- Fonctions Noyau : NuSVC peut utiliser différentes fonctions noyau telles que la fonction linéaire, la fonction de base radiale (RBF), la fonction polynomiale, etc. La fonction noyau détermine la façon dont l'espace des caractéristiques est transformé pour trouver l'hyper-plan de séparation.
Avantages de NuSVC :
- Efficacité dans les Espaces à Haute Dimension : NuSVC peut travailler efficacement dans des espaces à haute dimension, ce qui le rend adapté aux tâches comportant un grand nombre de caractéristiques.
- Robustesse face aux valeurs aberrantes : Les SVM, et NuSVC en particulier, sont résistants aux données aberrantes grâce à l'utilisation de vecteurs de support.
- Contrôle de la Complexité du Modèle : Le paramètre Nu permet de contrôler la complexité du modèle et d'équilibrer l'adaptation aux données et la généralisation.
- Bonne Généralisation : Les SVM et NuSVC, en particulier, font preuve d'une bonne généralisation, ce qui se traduit par d'excellentes performances sur des données nouvelles, jamais vues auparavant.
Limites de NuSVC :
- Inefficacité Avec de Grands Volumes de Données : NuSVC peut être inefficace lorsqu'il est entraîné sur de grands volumes de données en raison de la complexité des calculs.
- Réglage des Paramètres Requis : L'ajustement du paramètre Nu et de la fonction noyau peut nécessiter du temps et des ressources de calcul.
- Linéarité de la Fonction du Noyau : L'efficacité de NuSVC peut dépendre de manière significative du choix de la fonction noyau, et pour certaines tâches, il peut être nécessaire d'expérimenter différentes fonctions.
- Interprétabilité du Modèle : SVM et NuSVC fournissent d'excellents résultats, mais leurs modèles peuvent être complexes à interpréter, en particulier lorsque des noyaux non linéaires sont utilisés.
La classification vectorielle Nu-Support (NuSVC) est une méthode de classification puissante basée sur les SVM qui présente plusieurs avantages, notamment la robustesse aux valeurs aberrantes et une bonne généralisation. Mais son efficacité dépend de la sélection des paramètres et de la fonction du noyau, et elle peut être inefficace pour les grands volumes de données. Il est essentiel de sélectionner soigneusement les paramètres et d'adapter la méthode à des tâches de classification spécifiques.
2.3.1. Code de Création du Modèle de Classification NuSVC
Ce code démontre le processus d'entraînement d'un modèle de Classification NuSVC sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_NuSVC.py # The code demonstrates the process of training NuSVC model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.svm import NuSVC from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a NuSVC model nusvc_model = NuSVC(nu=0.5, kernel='linear') # train the model on the entire dataset nusvc_model.fit(X, y) # predict classes for the entire dataset y_pred = nusvc_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of NuSVC model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(nusvc_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "nusvc_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of NuSVC model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of NuSVC model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of NuSVC model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.96 0.96 50
Python 2 0.96 0.96 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\nusvc_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of NuSVC model in ONNX format: 0.9733333333333334
2.3.2. Code MQL5 pour Travailler avec le Modèle de Classification NuSVC
//+------------------------------------------------------------------+ //| Iris_NuSVC.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "nusvc_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="NuSVC"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_NuSVC (EURUSD,H1) model:NuSVC sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_NuSVC (EURUSD,H1) model:NuSVC sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_NuSVC (EURUSD,H1) model:NuSVC correct results: 97.33% Iris_NuSVC (EURUSD,H1) model=NuSVC all samples accuracy=0.973333 Iris_NuSVC (EURUSD,H1) model=NuSVC batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble des données d'Iris est de 97,33 %, ce qui correspond à la précision du modèle original.
2.3.3. Représentation ONNX du Modèle de Classification NuSVC
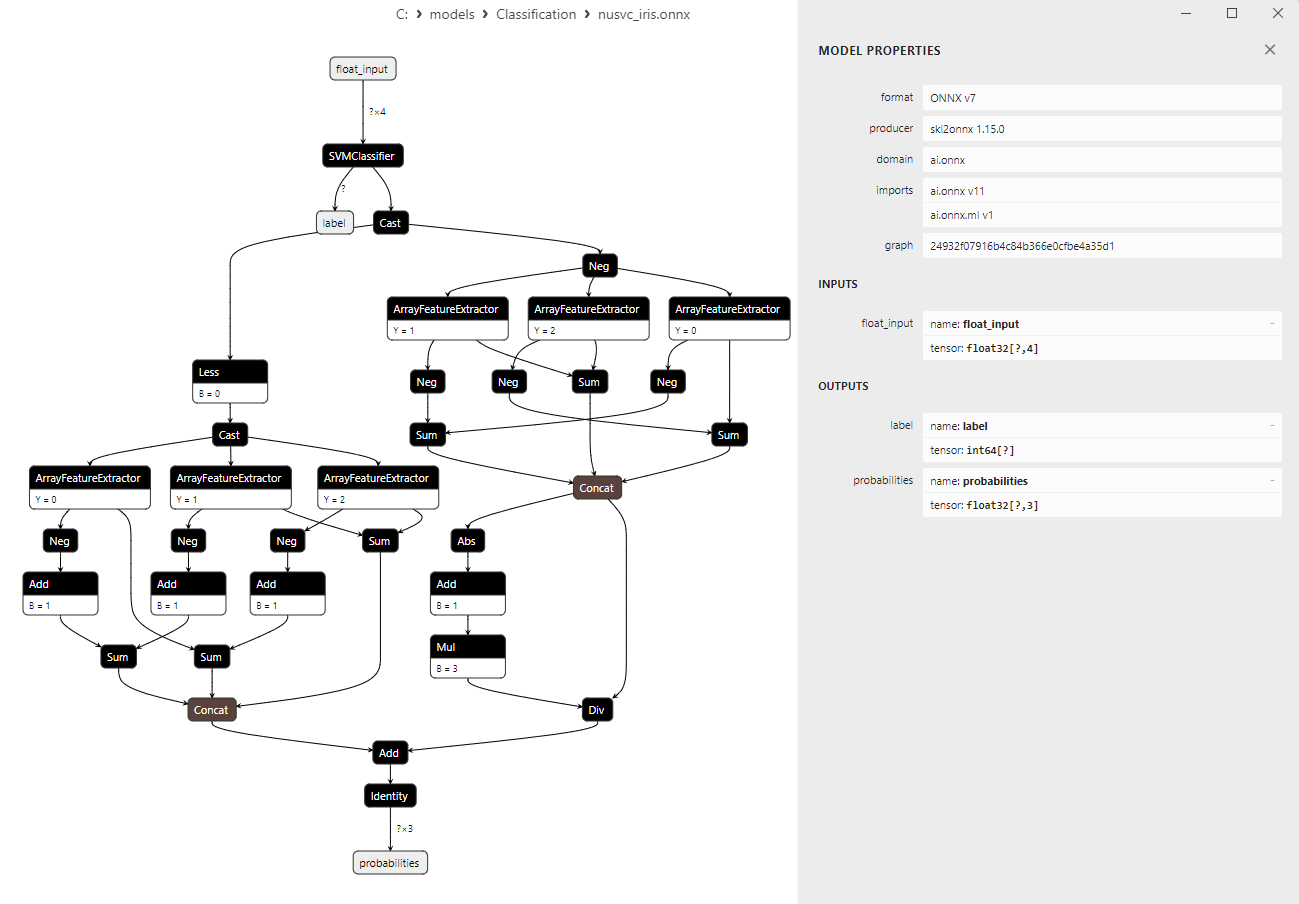
Figure 17. Représentation ONNX du Modèle de Classification NuSVC dans Netron
2.4. Classificateur Radius Neighbors
Le Classificateur Radius Neighbors est une méthode d'apprentissage automatique utilisée pour les tâches de classification basées sur le principe de proximité entre les objets. Contrairement au classique Classificateur K-NN (K-Nearest Neighbors), dans lequel un nombre fixe de voisins les plus proches (K) est choisi, dans le Classificateur Radius Neighbors, les objets sont classés en fonction de la distance qui les sépare des voisins les plus proches dans un rayon spécifié.Principes du Classificateur Radius Neighbors :
- Détermination du rayon : Le paramètre principal du Classificateur Radius Neighbors est le rayon, qui définit la distance maximale entre un objet et ses voisins pour qu'il soit considéré comme proche de la classe de ces derniers.
- Recherche des voisins les plus proches : La distance par rapport à tous les autres objets de l'ensemble de données d'apprentissage est calculée pour chaque objet. Les objets situés dans le rayon spécifié sont considérés comme voisins de l'objet.
- Vote : Le classificateur Radius Neighbors utilise le vote majoritaire parmi les voisins pour déterminer la classe de l'objet. Par exemple, si la majorité des voisins appartiennent à la classe A, l'objet sera également classé dans la classe A.
- Adaptabilité à la densité des données : Le Classificateur Radius Neighbors est adapté aux tâches où la densité des données dans les différentes régions de l'espace des caractéristiques peut varier.
- Capacité à travailler avec différentes formes de classes : Cette méthode donne de bons résultats dans les tâches où les classes ont des formes complexes et non linéaires.
- Convient aux données comportant des valeurs aberrantes : Le classificateur Radius Neighbors est plus robuste aux valeurs aberrantes que le K-NN car il ne tient pas compte des voisins situés au-delà du rayon spécifié.
- Sensibilité au choix du rayon : La sélection de la valeur optimale du rayon peut être une tâche non triviale et nécessite un réglage.
- Inefficacité sur les grands ensembles de données : Pour les grands ensembles de données, le calcul des distances entre tous les objets peut s'avérer très coûteux.
- Dépendance de la densité des données : Cette méthode peut être moins efficace lorsque les données n'ont pas une densité uniforme dans l'espace des caractéristiques.
Le Classificateur Radius Neighbors est une méthode d'apprentissage automatique précieuse dans les situations où la proximité des objets est importante et où les formes des classes peuvent être complexes. Il peut être appliqué dans divers domaines, notamment l'analyse d'images, le traitement du langage naturel, etc.
2.4.1. Code pour la Création d'un Modèle de Classification Radius Neighbors
Ce code démontre le processus d'entraînement d'un modèle de Classification Radius Neighbors sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_RadiusNeighborsClassifier.py # The code demonstrates the process of training an Radius Neughbors model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023 MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import RadiusNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Radius Neighbors Classifier model radius_model = RadiusNeighborsClassifier(radius=1.0) # train the model on the entire dataset radius_model.fit(X, y) # predict classes for the entire dataset y_pred = radius_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Radius Neighbors Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(radius_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "radius_neighbors_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Radius Neighbors Classifier model in ONNX format:", accuracy_onnx)
Résultats du script Iris_RadiusNeighbors.py :
Python Accuracy of Radius Neighbors Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.98 0.96 50
Python 2 0.98 0.94 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\radius_neighbors_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Radius Neighbors Classifier model in ONNX format: 0.9733333333333334
La précision du modèle original et la précision du modèle exporté au format ONNX sont identiques.
2.4.2. Code MQL5 pour Travailler avec le Modèle de Classification Radius Neighbors
//+------------------------------------------------------------------+ //| Iris_RadiusNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "radius_neighbors_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RadiusNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_RadiusNeighborsClassifier (EURUSD,H1) model:RadiusNeighborsClassifier correct results: 97.33% Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier all samples accuracy=0.973333 Iris_RadiusNeighborsClassifier (EURUSD,H1) model=RadiusNeighborsClassifier batch test accuracy=1.000000
Le modèle Classificateur Radius Neighbors a montré une précision de 97,33% avec 4 erreurs de classification (échantillons 78, 107, 127 et 139).
La précision du modèle ONNX exporté sur l'ensemble des données d'Iris est de 97,33 %, ce qui correspond à la précision du modèle original.
2.4.3 Représentation ONNX du Modèle de Classification Radius Neighbors
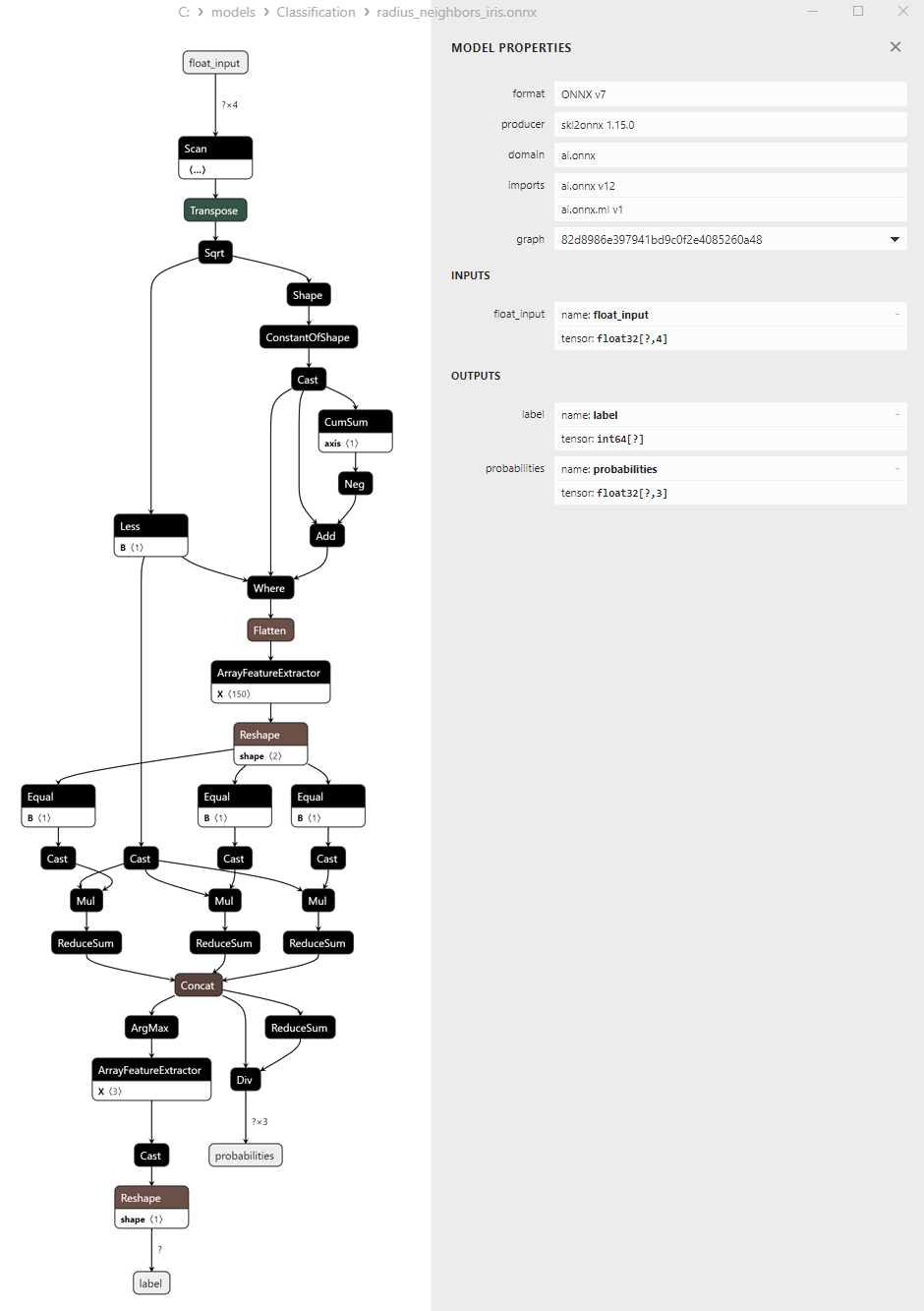
Figure 18. Représentation ONNX du Classificateur Radius Neighbors dans Netron
Note sur les méthodes RidgeClassifier et RidgeClassifierCV
RidgeClassifier et RidgeClassifierCV sont deux méthodes de classification basées sur la régression Ridge. Mais elles diffèrent dans la manière dont les paramètres sont réglés et les hyper-paramètres sont automatiquement sélectionnés :
RidgeClassifier :
- RidgeClassifier est une méthode de classification basée sur la régression Ridge, utilisée pour les tâches de classification binaire et multi-classe.
- Dans le cas de la classification multi-classe, RidgeClassifier convertit la tâche en plusieurs tâches binaires (un contre tous) et construit un modèle pour chacune d'entre elles.
- Le paramètre de régularisation alpha doit être réglé manuellement par l'utilisateur, ce qui signifie que vous devez choisir la valeur alpha optimale par le biais d'expériences ou d'analyses de données de validation.
RidgeClassifierCV :
- RidgeClassifierCV est une extension de RidgeClassifier qui fournit un support intégré pour la validation croisée et la sélection automatique du paramètre de régularisation optimal alpha.
- Au lieu de définir manuellement alpha, vous pouvez fournir à RidgeClassifierCV une liste de valeurs alpha à étudier et spécifier la méthode de validation croisée (par exemple, via le paramètre cv).
- RidgeClassifierCV sélectionne automatiquement la valeur alpha optimale qui donne les meilleurs résultats lors de la validation croisée.
La principale différence entre eux réside donc dans le niveau d'automatisation de la sélection de la valeur optimale du paramètre de régularisation alpha. RidgeClassifier nécessite un réglage manuel de l'alpha, alors que RidgeClassifierCV permet une sélection automatique de la valeur alpha optimale par validation croisée. Le choix de l'un ou l'autre dépend de vos besoins et de votre désir d'automatiser le processus de mise au point du modèle.
2.5. Classificateur Ridge
Le classificateur Ridge est une variante de la régression logistique qui inclut la régularisation L2 (Régression Ridge) dans le modèle. La régularisation L2 ajoute une pénalité aux grands coefficients du modèle, ce qui permet de réduire l'ajustement excessif et d'améliorer la capacité de généralisation du modèle.
Principes du Classificateur Ridge :
- Prédiction des Probabilités : À l'instar de la régression logistique, le Classificateur Ridge modélise la probabilité qu'un objet appartienne à une classe spécifique à l'aide d'une fonction logistique (sigmoïde).
- Régularisation L2 : Le Classificateur Ridge ajoute un terme de régularisation L2 qui pénalise les coefficients importants du modèle. Cela permet de contrôler la complexité du modèle et de réduire l'ajustement excessif.
- Formation des Paramètres : Le modèle Classificateur Ridge est entraîné sur l'ensemble de données d'entraînement afin d'ajuster les poids (coefficients) des caractéristiques et le paramètre de régularisation.
Avantages du Classificateur Ridge :
- Réduction de l'Ajustement Excessif : La régularisation L2 permet de réduire la tendance du modèle à se sur-adapter, ce qui est particulièrement utile lorsque les données sont limitées.
- Traitement de la Multi-colinéarité : Le Classificateur Ridge gère bien les problèmes de multi-colinéarité, lorsque les caractéristiques sont fortement corrélées entre elles.
Limites du Classificateur Ridge :
- Sensibilité au Choix du Paramètre de Régularisation : Comme pour les autres méthodes de régularisation, le choix de la bonne valeur pour le paramètre de régularisation (alpha) nécessite un réglage et une évaluation.
- Contrainte de Classification Multi-classe : Le classificateur Ridge est initialement conçu pour la classification binaire. Mais il peut être adapté à la classification multi-classe à l'aide d'approches telles que One-vs-All.
Le Classificateur Ridge est une puissante méthode d'apprentissage automatique qui combine les avantages de la régression logistique avec la régularisation pour lutter contre l'ajustement excessif et améliorer la capacité de généralisation du modèle. Il trouve des applications dans divers domaines où la classification probabiliste et le contrôle de la complexité des modèles sont importants.
2.5.1. Code de Création du Modèle Classificateur Ridge
Ce code démontre le processus d'entraînement du modèle Classificateur Ridge sur le jeu de données Iris, son export au format ONNX, et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_RidgeClassifier.py # The code demonstrates the process of training Ridge Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Ridge Classifier model ridge_model = RidgeClassifier() # train the model on the entire dataset ridge_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Ridge Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Ridge Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Ridge Classifier model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Ridge Classifier model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of Ridge Classifier model in ONNX format: 0.8533333333333334
2.5.2. Code MQL5 pour Travailler avec le Modèle de Classification Ridge
//+------------------------------------------------------------------+ //| Iris_RidgeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier correct results: 85.33% Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier all samples accuracy=0.853333 Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifier (EURUSD,H1) model:RidgeClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifier (EURUSD,H1) model=RidgeClassifier batch test accuracy=0.000000
Sur l'ensemble des données d'Iris, le modèle a démontré une précision de 85,33 %, ce qui correspond à la précision de l'original.
2.5.3. Représentation ONNX du Modèle de Classification Ridge
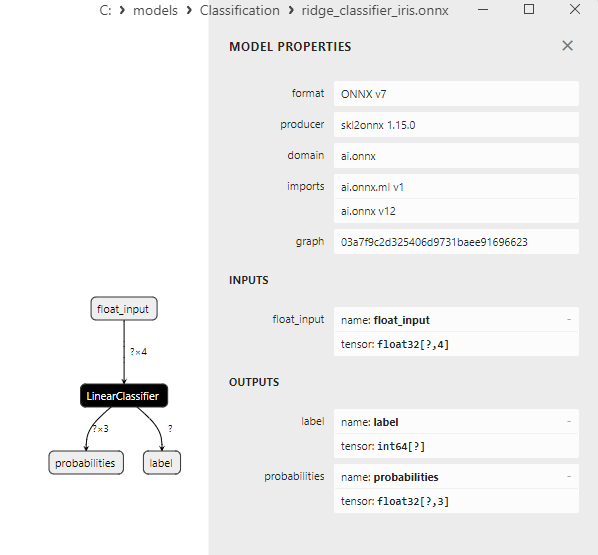
Figure 19. Représentation ONNX du Modèle de Classification Ridge dans Netron
2.6. RidgeClassifierCV
La méthode de classification RidgeClassifierCV est un puissant algorithme de classification binaire et multi-classe basé sur la régression Ridge.
Principes de RidgeClassifierCV :
- Régression Linéaire Ridge : RidgeClassifierCV est basé sur la régression linéaire Ridge. Cette méthode est une modification de la régression linéaire à laquelle on ajoute une régularisation L2. La régularisation permet de contrôler le sur-ajustement en réduisant l'ampleur des poids des caractéristiques.
- Classification Binaire et Multi-classe : RidgeClassifierCV peut être utilisé pour la classification binaire (lorsqu'il n'y a que deux classes) et la classification multi-classe (lorsqu'il y a plus de 2 classes). Pour la classification multi-classe, il convertit la tâche en plusieurs tâches binaires (un contre tous) et construit un modèle pour chacune d'entre elles.
- Sélection Automatique du Paramètre de Régularisation : L'un des principaux avantages du RidgeClassifierCV est sa prise en charge intégrée de la validation croisée et la sélection automatique du paramètre de régularisation optimal alpha. Au lieu de régler manuellement alpha, la méthode itère sur différentes valeurs alpha et sélectionne la meilleure sur la base d'une validation croisée.
- Traitement de la Multi-colinéarité : La régression ridge gère bien les problèmes de multi-colinéarité, lorsque les caractéristiques sont fortement corrélées entre elles. La régularisation permet de contrôler la contribution de chaque caractéristique, ce qui rend le modèle robuste aux données corrélées.
Avantages de RidgeClassifierCV :
- Sélection Automatique des Hyper-paramètres : L'un des principaux avantages de RidgeClassifierCV est sa capacité à sélectionner automatiquement la valeur alpha optimale à l'aide de la validation croisée. Il n'est donc pas nécessaire d'expérimenter différentes valeurs alpha, ce qui augmente les chances d'obtenir de bons résultats.
- Contrôle du Sur-Ajustement : La régularisation L2 fournie par RidgeClassifierCV permet de contrôler la complexité du modèle et de réduire le risque de sur-ajustement. Ceci est particulièrement important pour les tâches dont les données sont limitées.
- Transparence et Interprétabilité : RidgeClassifierCV fournit des poids interprétables pour les caractéristiques, ce qui permet d'analyser la contribution de chaque caractéristique aux prédictions et de tirer des conclusions sur l'importance des caractéristiques.
- Efficacité : La méthode est très efficace et peut être appliquée à de grands ensembles de données.
Limites de RidgeClassifierCV :
- Linéarité : RidgeClassifierCV suppose des relations linéaires entre les caractéristiques et la variable cible. Si les données présentent de fortes relations non linéaires, la méthode peut ne pas être suffisamment précise.
- Sensibilité à la Mise à l'Echelle des Caractéristiques : La méthode est sensible à la mise à l'échelle des caractéristiques. Il est recommandé de normaliser les caractéristiques avant d'appliquer RidgeClassifierCV.
- Sélection Optimale des Caractéristiques : RidgeClassifierCV n'effectue pas de sélection automatique des caractéristiques. Vous devez donc décider manuellement des caractéristiques à inclure dans le modèle.
La méthode de classification RidgeClassifierCV est un outil puissant pour la classification binaire et multi-classe avec sélection automatique du paramètre de régularisation optimal. Son contrôle du sur-ajustement, sa facilité d'interprétation et son efficacité en font un choix populaire pour diverses tâches de classification. Mais il est important de garder à l'esprit ses limites, en particulier l'hypothèse de relations linéaires entre les caractéristiques et la variable cible.
2.6.1. Code de Création du Modèle RidgeClassifierCV
Ce code démontre le processus d'entraînement du modèle RidgeClassifierCV sur le jeu de données Iris, son export au format ONNX et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_RidgeClassifierCV.py # The code demonstrates the process of training RidgeClassifierCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import RidgeClassifierCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a RidgeClassifierCV model ridge_classifier_cv_model = RidgeClassifierCV() # train the model on the entire dataset ridge_classifier_cv_model.fit(X, y) # predict classes for the entire dataset y_pred = ridge_classifier_cv_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of RidgeClassifierCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(ridge_classifier_cv_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "ridge_classifier_cv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of RidgeClassifierCV model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of RidgeClassifierCV model: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of RidgeClassifierCV model in ONNX format: 0.8533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.66 0.75 50
Python 2 0.73 0.90 0.80 50
Python
Python accuracy 0.85 150
Python macro avg 0.86 0.85 0.85 150
Python weighted avg 0.86 0.85 0.85 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\ridge_classifier_cv_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Name: label, Data Type: tensor(int64), Shape: [None]
Python 2. Name: probabilities, Data Type: tensor(float), Shape: [None, 3]
Python
Python Accuracy of RidgeClassifierCV model in ONNX format: 0.8533333333333334
2.6.2. Code MQL5 pour Travailler avec le Modèle RidgeClassifierCV
//+------------------------------------------------------------------+ //| Iris_RidgeClassifierCV.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "ridge_classifier_cv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- ulong input_shape[]= { batch_size, input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- int output1[]; float output2[][3]; //--- ArrayResize(output1,(int)batch_size); ArrayResize(output2,(int)batch_size); //--- ulong output_shape[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {batch_size,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output1,output2); //--- classes are ready in output1[k]; if(res) { for(int k=0; k<(int)batch_size; k++) model_classes_id[k]=output1[k]; } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RidgeClassifierCV"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV correct results: 85.33% Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV all samples accuracy=0.853333 Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_RidgeClassifierCV (EURUSD,H1) model:RidgeClassifierCV FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_RidgeClassifierCV (EURUSD,H1) model=RidgeClassifierCV batch test accuracy=0.000000
La performance du modèle ONNX correspond également parfaitement à la performance du modèle scikit-learn original (85,33%).
2.6.3. Représentation ONNX du Modèle RidgeClassifierCV
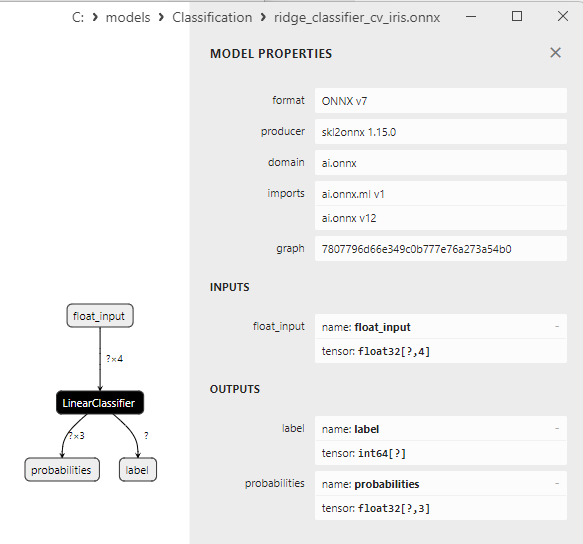
Figure 20. Représentation ONNX du RidgeClassifierCV dans Netron
2.7. Classificateur Random Forest
Le Classificateur Random Forest est une méthode d'apprentissage automatique d'ensemble basée sur la construction de plusieurs arbres de décision et la combinaison de leurs résultats pour améliorer la qualité de la classification. Cette méthode est extrêmement populaire en raison de son efficacité et de sa capacité à travailler avec des données diverses.
Principes du Classificateur Random Forest :
- Bagging (Bootstrap Aggregating) : Random Forest utilise la méthode du bagging, qui consiste à créer de multiples sous-échantillons (échantillons bootstrap) à partir des données d'apprentissage avec remplacement. Pour chaque sous-échantillon, un arbre de décision distinct est construit.
- Sélection Aléatoire des Caractéristiques : Lors de la construction de chaque arbre, un sous-ensemble aléatoire de caractéristiques est sélectionné parmi l'ensemble des caractéristiques. Cela favorise la diversité entre les arbres et réduit les corrélations entre eux.
- Vote : Lors de la classification d'un objet, chaque arbre fournit sa propre prédiction et la classe qui reçoit la majorité des votes de tous les arbres est choisie comme prédiction finale du modèle.
Avantages du Classificateur Random Forest :
- Haute Précision : Random Forest atteint généralement une grande précision de classification en faisant la moyenne des résultats de plusieurs arbres.
- Capacité à Traiter des Données Diverses : Il fonctionne bien avec des caractéristiques numériques et catégorielles, ainsi qu'avec des données de structures variées.
- Résistance au Sur-Ajustement : Random Forest dispose d'une régularisation intégrée, ce qui le rend résistant à l'ajustement excessif.
- Importance de la Fonction : Random Forest peut évaluer l'importance des caractéristiques, aidant ainsi les data scientists et les feature engineers à mieux comprendre les données.
Limites du Classificateur Random Forest :
- Complexité de Calcul : L'apprentissage d'une Forêt Aléatoire peut prendre beaucoup de temps, surtout avec un grand nombre d'arbres et de caractéristiques.
- Défis en Matière d'Interprétabilité : En raison du grand nombre d'arbres et de la sélection aléatoire des caractéristiques, l'interprétation des modèles peut s'avérer difficile.
- Pas de Garantie de Robustesse des Valeurs Aberrantes : Random Forest n'est pas toujours robuste face aux données aberrantes.
Le Classificateur Random Forest est un puissant algorithme d'apprentissage automatique largement utilisé dans divers domaines, notamment la biomédecine, l'analyse financière et l'analyse de données textuelles. Il excelle dans la résolution des tâches de classification et de régression et possède une grande capacité de généralisation.
2.7.1. Code de Création du Modèle de Classification Random Forest
Ce code démontre le processus d'entraînement du modèle Classificateur Random Forest sur le jeu de données Iris, son export au format ONNX, et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_RandomForestClassifier.py # The code demonstrates the process of training Random Forest Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023,2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Random Forest Classifier model rf_model = RandomForestClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset rf_model.fit(X, y) # predict classes for the entire dataset y_pred = rf_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Random Forest Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(rf_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "rf_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Random Forest Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Random Forest Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\rf_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Random Forest Classifier model in ONNX format: 1.0
Le modèle de Classification Random Forest (et sa version ONNX) résout le problème de classification de l'Iris de Fisher avec une précision de 100%.
2.7.2. Code MQL5 pour Travailler avec le Modèle de Classification Random Forest
//+------------------------------------------------------------------+ //| Iris_RandomForestClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "rf_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="RandomForestClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_RandomForestClassifier (EURUSD,H1) model:RandomForestClassifier correct results: 100.00% Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier all samples accuracy=1.000000 Iris_RandomForestClassifier (EURUSD,H1) model=RandomForestClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble des données d'Iris est de 100%, ce qui correspond à la précision du modèle original.
2.7.3. Représentation ONNX du Modèle de Classification Random Forest
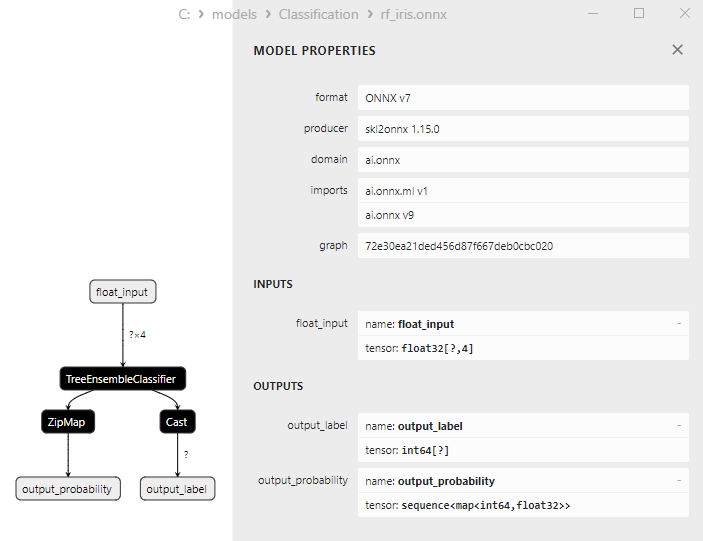
Figure 21. Représentation ONNX du Modèle de Classification Random Forest dans Netron
2.8. Classificateur Gradient Boosting
Gradient Boosting est l'une des méthodes d'apprentissage automatique les plus puissantes et trouve des applications dans divers domaines, notamment l'analyse de données, la vision par ordinateur, le traitement du langage naturel et l'analyse financière, grâce à sa grande précision et à sa capacité à travailler avec des données diverses. Le Classificateur Gradient Boosting est une méthode d'apprentissage automatique d'ensemble qui crée une composition d'arbres de décision pour résoudre les tâches de classification. Cette méthode est appréciée pour sa capacité à atteindre une grande précision et sa résistance à l'ajustement excessif.
Principes du Classificateur Gradient Boosting :
- Ensemble d'Arbres de Décision : Le Classificateur Gradient Boosting construit un ensemble d'arbres de décision, où chaque arbre vise à améliorer les prédictions de l'arbre précédent.
- Descente en Gradient : Gradient Boosting utilise la descente de gradient pour optimiser la fonction de perte. Il minimise l'erreur de classification en calculant le gradient de la fonction de perte et en actualisant les prédictions sur la base de ce gradient.
- Pondération des Arbres : Chaque arbre de la composition a un poids et, à la fin, les prédictions de tous les arbres sont combinées en tenant compte de leurs poids.
Avantages du Classificateur Gradient Boosting :
- Haute Précision : Le Classificateur Gradient Boosting offre généralement une grande précision de classification et constitue l'une des méthodes d'apprentissage automatique les plus puissantes.
- Résistance au Sur-Ajustement : Grâce à l'utilisation de la régularisation et de la descente de gradient, cette méthode est résistante au sur-ajustement, en particulier lors de l'ajustement des hyper-paramètres.
- Capacité à Travailler avec Différents Types de Données : Le Classificateur Gradient Boosting peut traiter différents types de données, y compris des caractéristiques numériques et catégorielles.
Limites du Classificateur Gradient Boosting :
- Complexité de Calcul : L'apprentissage du Classificateur Gradient Boosting peut être très gourmand en ressources informatiques, en particulier avec un grand nombre d'arbres ou d'arbres profonds.
- Défis en Matière d'Interprétabilité : En raison de la complexité de la composition de plusieurs arbres, l'interprétation des résultats peut s'avérer difficile.
- Pas toujours adapté aux petits ensembles de données : Le renforcement du gradient nécessite généralement une quantité importante de données pour fonctionner efficacement et peut être sujet à un sur-ajustement sur de petits ensembles de données.
Le Classificateur Gradient Boosting est une puissante méthode d'apprentissage automatique souvent utilisée dans les concours d'analyse de données, qui permet de résoudre efficacement diverses tâches de classification. Il permet de découvrir des relations non linéaires complexes dans les données et présente une bonne généralisation lorsque les hyper-paramètres sont correctement réglés.
2.8.1. Code de Création du Modèle de Classification Gradient Boosting
Ce code démontre le processus d'entraînement du modèle Classificateur Gradient Boosting sur le jeu de données Iris, son export au format ONNX, et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_GradientBoostingClassifier.py # The code demonstrates the process of training Gradient Boostring Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import GradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gradient Boosting Classifier model gb_model = GradientBoostingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset gb_model.fit(X, y) # predict classes for the entire dataset y_pred = gb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gradient Boosting Classifier model in ONNX format: 1.0
La précision du modèle ONNX exporté sur l'ensemble des données d'Iris est de 100%, ce qui correspond à la précision du modèle original.
2.8.2. Code MQL5 pour Travailler avec le Modèle de Classification Gradient Boosting
//+------------------------------------------------------------------+ //| Iris_GradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_GradientBoostingClassifier (EURUSD,H1) model:GradientBoostingClassifier correct results: 100.00% Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier all samples accuracy=1.000000 Iris_GradientBoostingClassifier (EURUSD,H1) model=GradientBoostingClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble des données d'Iris est de 100%, ce qui correspond à la précision du modèle original.
2.8.3. Représentation ONNX du Modèle de Classification Gradient Boosting
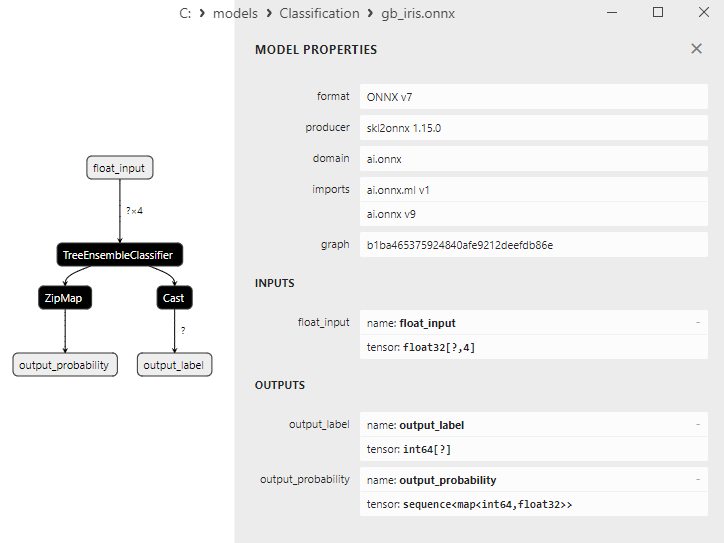
Figure 22. Représentation ONNX du Modèle de Classification Gradient Boosting dans Netron
2.9. Classificateur Adaptative Boosting
Le Classificateur AdaBoost (Adaptive Boosting) est une méthode d'apprentissage automatique d'ensemble utilisée pour améliorer la classification en combinant les résultats de plusieurs classificateurs faibles (par exemple, des arbres de décision) pour créer un algorithme plus puissant.
Principes du Classificateur AdaBoost :
- Ensemble de Classificateurs Faibles : AdaBoost commence par initialiser les poids de chaque échantillon de l'ensemble de formation, en leur attribuant des valeurs initiales égales.
- Formation de Classificateurs Faibles : AdaBoost entraîne ensuite un classificateur faible (par exemple, un arbre de décision) sur l'ensemble d'apprentissage en tenant compte des poids de l'échantillon. Ce classificateur tente de classer correctement les échantillons.
- Redistribution des Poids : AdaBoost ajuste les poids des échantillons, en augmentant les poids des échantillons mal classés et en diminuant les poids des échantillons correctement classés.
- Création de la Composition : AdaBoost répète plusieurs fois le processus de formation des classificateurs faibles et de redistribution des poids. Les résultats de ces classificateurs faibles sont ensuite combinés dans une composition, chaque classificateur contribuant en fonction de sa précision.
Avantages du Classificateur AdaBoost :
- Haute Précision : AdaBoost fournit généralement une précision de classification élevée en combinant plusieurs classificateurs faibles.
- Résistance au Sur-Ajustement : AdaBoost dispose d'une régularisation intégrée, ce qui le rend résistant au sur-ajustement.
- Capacité à travailler avec différents classificateurs : AdaBoost peut utiliser différents classificateurs de base, ce qui permet de l'adapter à des tâches spécifiques.
Limites du Classificateur AdaBoost :
- Sensibilité aux Valeurs Aberrantes : AdaBoost peut être sensible aux valeurs aberrantes dans les données, car elles peuvent avoir un poids important.
- N'est pas toujours adapté aux tâches complexes : Dans certaines tâches complexes, AdaBoost peut nécessiter un grand nombre de classificateurs de base pour obtenir de bons résultats.
- Dépendance à l'égard de la qualité des classificateurs de base : AdaBoost est plus performant lorsque les classificateurs de base sont meilleurs que les suppositions aléatoires.
Le classificateur AdaBoost est un puissant algorithme d'apprentissage automatique couramment utilisé dans la pratique pour résoudre les tâches de classification. Il est bien adapté aux problèmes binaires et multi-classes et peut être adapté à divers classificateurs de base.
2.9.1. Code de Création du Modèle de Classificateur Adaptative Boosting
Ce code démontre le processus d'entraînement du modèle de Classificateur Adaptive Boosting sur le jeu de données Iris, son export au format ONNX, et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_AdaBoostClassifier.py # The code demonstrates the process of training AdaBoost Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import AdaBoostClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an AdaBoost Classifier model adaboost_model = AdaBoostClassifier(n_estimators=50, random_state=42) # train the model on the entire dataset adaboost_model.fit(X, y) # predict classes for the entire dataset y_pred = adaboost_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of AdaBoost Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(adaboost_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "adaboost_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of AdaBoost Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of AdaBoost Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.92 0.96 0.94 50
Python 2 0.96 0.92 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\adaboost_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of AdaBoost Classifier model in ONNX format: 0.96
2.9.2. Code MQL5 pour Travailler avec le Modèle de Classification Adaptive Boosting
//+------------------------------------------------------------------+ //| Iris_AdaBoostClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "adaboost_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="AdaBoostClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AdaBoostClassifier (EURUSD,H1) model:AdaBoostClassifier correct results: 96.00% Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier all samples accuracy=0.960000 Iris_AdaBoostClassifier (EURUSD,H1) model=AdaBoostClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 96%, ce qui correspond à la précision du modèle original.
2.9.3. Représentation ONNX du Modèle de Classification Adaptative Boosting
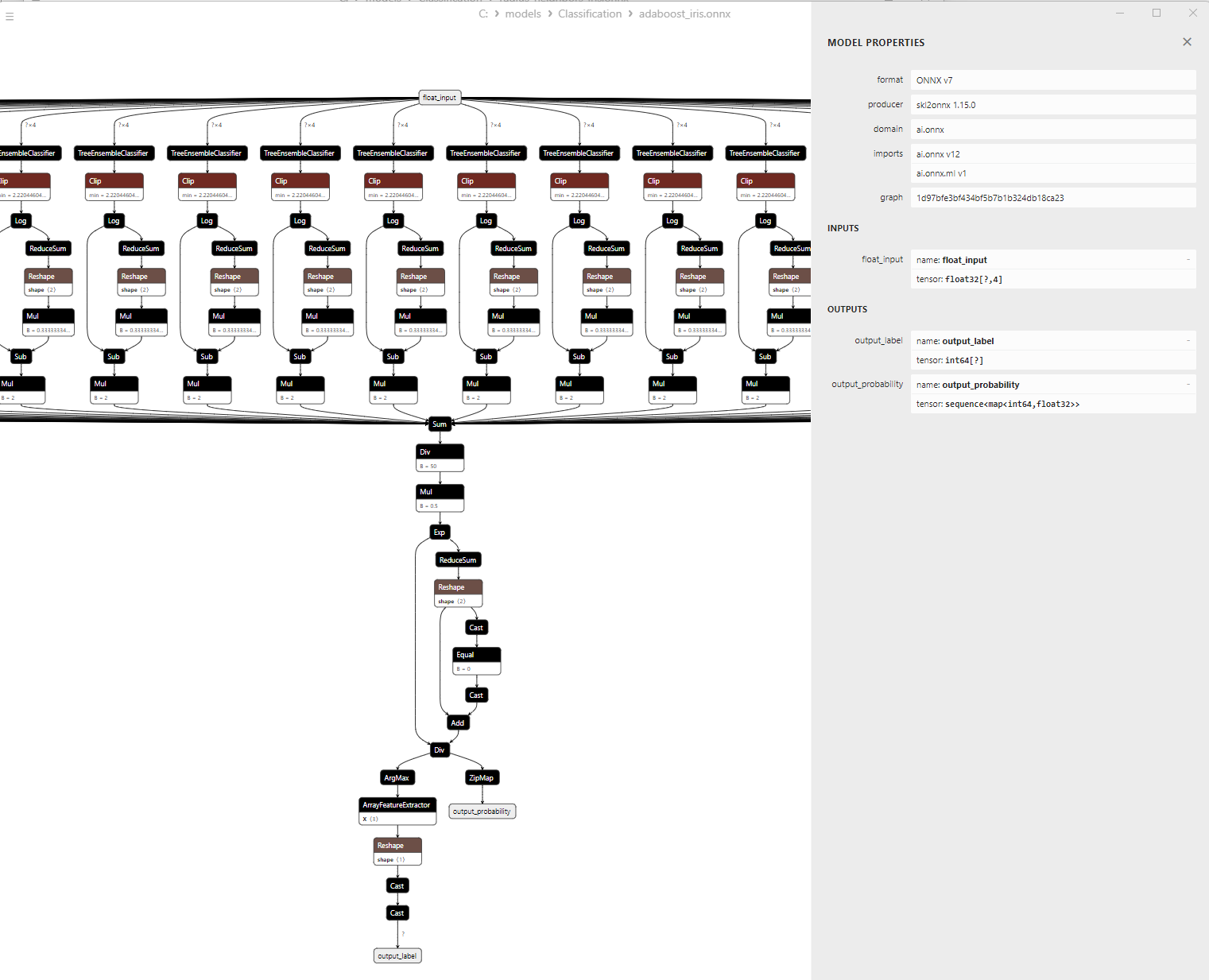
Figure 23. Représentation ONNX du Classificateur Adaptative Boosting dans Netron
2.10. Classificateur Bootstrap Aggregating
Le classificateur Bagging (Bootstrap Aggregating) est une méthode d'apprentissage automatique d'ensemble qui repose sur la création de plusieurs sous-échantillons aléatoires (échantillons bootstrap) à partir des données d'apprentissage et sur l'élaboration de modèles distincts pour chacun d'entre eux. Les résultats sont ensuite combinés pour améliorer la capacité de généralisation du modèle.
Principes du Classificateur Bagging :
- Création de Sous-Echantillons : L'échantillonnage commence par la création de plusieurs sous-échantillons aléatoires (échantillons bootstrap) à partir des données d'apprentissage, avec remplacement. Cela signifie que les mêmes échantillons peuvent apparaître dans plusieurs sous-échantillons et que certains échantillons peuvent être omis.
- Formation des Modèles de Base : Pour chaque sous-échantillon, un modèle de base distinct (par exemple, un arbre de décision) est formé. Chaque modèle est formé indépendamment des autres.
- Agrégation des Résultats : Après l'entraînement de tous les modèles de base, les résultats de leurs prédictions sont combinés pour obtenir la prédiction finale. Dans la classification binaire, cela peut se faire par le biais d'un vote à la majorité.
Avantages de la Classification Bagging :
- Variance Réduite : Le bagging réduit la variance du modèle en faisant la moyenne des résultats de plusieurs modèles de base, ce qui peut conduire à des prédictions plus stables et plus fiables.
- Réduction de l'Ajustement Excessif : Étant donné que chaque modèle de base est formé sur différents sous-échantillons, le Bagging peut réduire la tendance du modèle à se sur-adapter.
- Polyvalence : L'agrégation peut utiliser différents modèles de base, ce qui permet de l'adapter à différents types de données et de tâches.
Limites de la Classification Bagging :
- N'améliore pas la partialité : Bagging tend à réduire la variance, mais ne résout pas le biais du modèle. Si les modèles de base ont tendance à être biaisés (par exemple, sous-adaptation), Bagging ne corrigera pas ce problème.
- N'est pas toujours adapté aux tâches complexes : Dans certaines tâches complexes, le Bagging peut nécessiter un grand nombre de modèles de base pour obtenir de bons résultats.
Le Classificateur Bagging est une méthode d'apprentissage automatique efficace qui permet d'améliorer la capacité de généralisation du modèle et de réduire le sur-ajustement. Il est souvent utilisé en combinaison avec différents modèles de base pour répondre à diverses tâches de classification et de régression.
2.10.1. Code de Création du Modèle de Classification Bootstrap Aggregating
Ce code démontre le processus d'entraînement du modèle de Classification Bootstrap Aggregating sur le jeu de données Iris, son export au format ONNX, et la réalisation de la classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_BootstrapAggregatingClassifier.py # The code demonstrates the process of training Bagging Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import BaggingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bagging Classifier model with a Decision Tree base estimator bagging_model = BaggingClassifier(n_estimators=100, random_state=42) # train the model on the entire dataset bagging_model.fit(X, y) # predict classes for the entire dataset y_pred = bagging_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bagging Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bagging_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bagging_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bagging Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Bagging Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bagging_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bagging Classifier model in ONNX format: 1.0
Le modèle Bootstrap Aggregating Classifier (et sa version ONNX) a atteint une précision de 100% dans la classification de l'ensemble de données Iris.
2.10.2. Code MQL5 pour Travailler avec le Modèle Bootstrap Aggregating Classifier
//+------------------------------------------------------------------+ //| Iris_BootstrapAggregatingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bagging_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BootstrapAggregatingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_BootstrapAggregatingClassifier (EURUSD,H1) model:BootstrapAggregatingClassifier correct results: 100.00% Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier all samples accuracy=1.000000 Iris_BootstrapAggregatingClassifier (EURUSD,H1) model=BootstrapAggregatingClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 100%, ce qui correspond à la précision du modèle original.
2.10.3. Représentation ONNX du Classificateur Bootstrap Aggregating
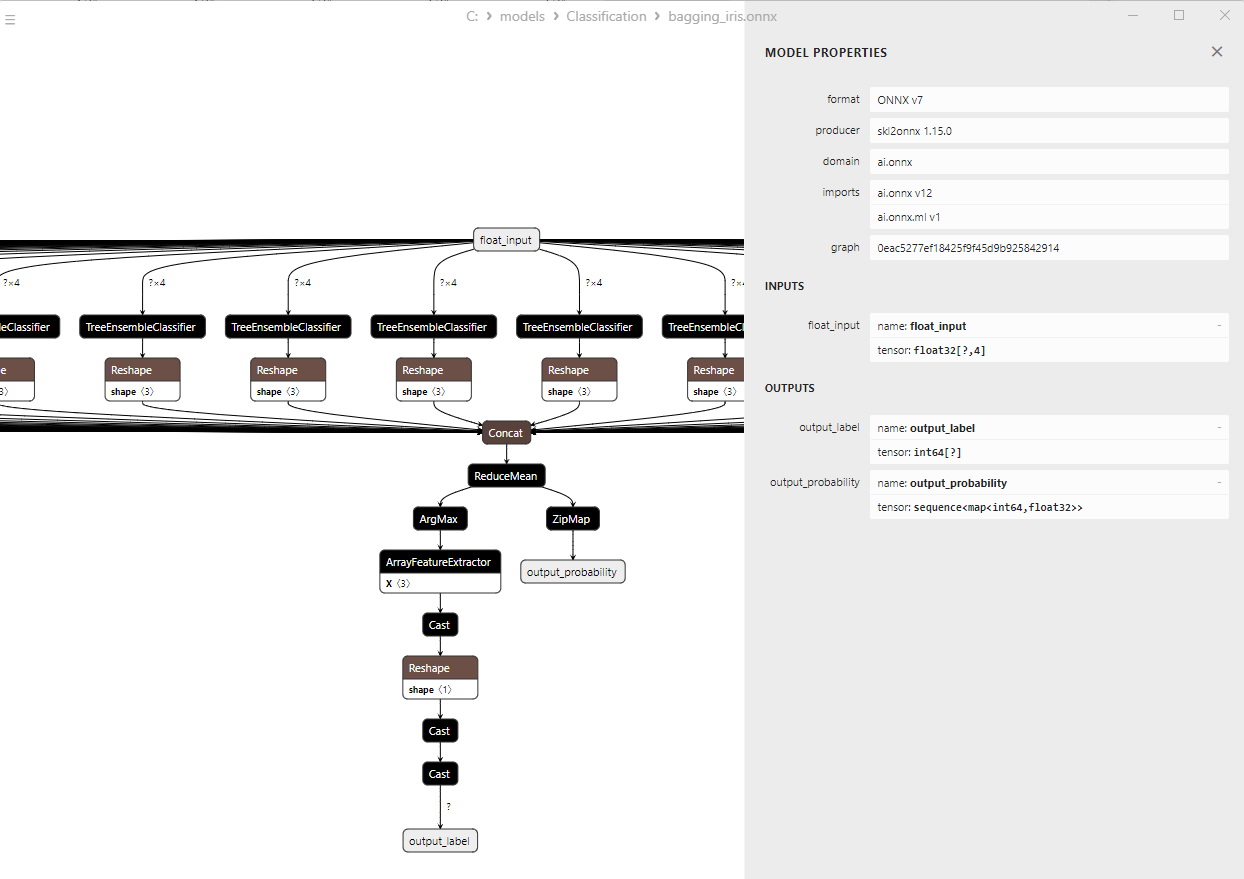
Figure 24. Représentation ONNX du Classificateur Bootstrap Aggregating dans Netron
2.11. Classificateur K-Nearest Neighbors (K-NN)
Le classificateur K-Nearest Neighbors (K-NN) est une méthode d'apprentissage automatique utilisée pour résoudre les tâches de classification et de régression basées sur la similarité entre les points de données. Elle repose sur le principe selon lequel les objets proches les uns des autres dans un espace multidimensionnel présentent des caractéristiques similaires et peuvent donc avoir des étiquettes de classe similaires.
Principes du Classificateur K-NN :
- Déterminer la Proximité : Le classificateur K-NN calcule la proximité entre l'objet à classer et les autres objets de l'ensemble de données d'apprentissage. Pour cela, on utilise souvent une mesure de distance, telle que la distance euclidienne ou la distance de Manhattan.
- Choix du nombre de voisins : Le paramètre K détermine le nombre de plus proches voisins à utiliser pour classer un objet. En règle générale, K est choisi en fonction de la tâche et des données.
- Vote : K-NN utilise le vote majoritaire parmi les K voisins les plus proches pour déterminer la classe de l'objet. Par exemple, si la majorité des K voisins appartiennent à la classe A, l'objet sera également classé dans la classe A.
Avantages du Classificateur K-NN :
- Simplicité et intuitivité : K-NN est une méthode simple et intuitive, facile à comprendre et à appliquer.
- Capacité à travailler avec différents types de données : K-NN peut être utilisé pour différents types de données, notamment les données numériques, catégorielles et textuelles.
- Adaptabilité à l'évolution des données : K-NN peut s'adapter rapidement aux changements dans les données, ce qui le rend approprié pour les tâches avec des données dynamiques.
Limites du Classificateur K-NN :
- Sensibilité au choix de K : La sélection de la valeur optimale de K peut être une tâche non triviale. Un petit K peut conduire à un sur-ajustement, alors qu'un grand K peut conduire à un sous-ajustement.
- Sensibilité à la mise à l'échelle des caractéristiques : K-NN est sensible à la mise à l'échelle des caractéristiques, c'est pourquoi la normalisation des données peut s'avérer importante.
- Complexité de calcul : Pour les grands ensembles de données et un grand nombre de caractéristiques, le calcul des distances entre toutes les paires d'objets peut s'avérer très coûteux.
- Manque d'interprétabilité : Les résultats de K-NN peuvent être difficiles à interpréter, en particulier lorsque K est grand et qu'il y a beaucoup de données.
Le Classificateur K-NN est une méthode d'apprentissage automatique qui peut être utile dans les tâches où la proximité des objets est essentielle, comme les systèmes de recommandation, la classification des textes et la reconnaissance des formes. Il est bien adapté à l'analyse initiale des données et au prototypage rapide de modèles.
2.11.1. Code de Création du Modèle de Classificateur K-Nearest Neighbors (K-NN)
Ce code démontre le processus d'entraînement d'un modèle de Classification K-NN (K-Nearest Neighbors) sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_KNearestNeighborsClassifier.py # The code uses the K-Nearest Neighbors (KNN) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neighbors import KNeighborsClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a K-Nearest Neighbors (KNN) Classifier model knn_model = KNeighborsClassifier(n_neighbors=3) # train the model on the entire dataset knn_model.fit(X, y) # predict classes for the entire dataset y_pred = knn_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of KNN Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(knn_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "knn_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of KNN Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of KNN Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\knn_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of KNN Classifier model in ONNX format: 0.96
2.11.2. Code MQL5 pour Travailler avec le Modèle de Classification K-NN (K-Nearest Neighbors)
//+------------------------------------------------------------------+ //| Iris_KNearestNeighborsClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "knn_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="KNearestNeighborsClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier correct results: 96.00% Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier all samples accuracy=0.960000 Iris_KNearestNeighborsClassifier (EURUSD,H1) model:KNearestNeighborsClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_KNearestNeighborsClassifier (EURUSD,H1) model=KNearestNeighborsClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 96%, ce qui est cohérent avec la précision du modèle original.
2.11.3. Représentation ONNX du Classificateur K-NN (K-NN)
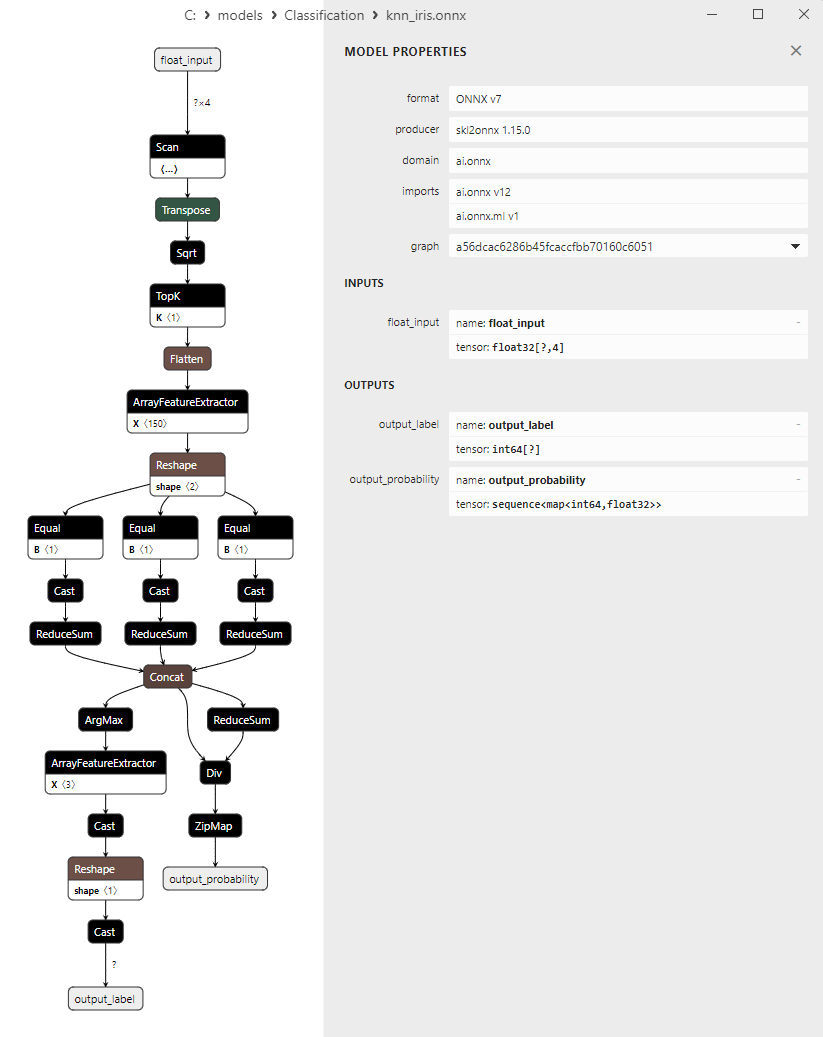
Figure 25. Représentation ONNX des K-Nearest Neighbors dans Netron
2.12. Classificateur Decision Tree
Le Classificateur Decision Tree est une méthode d'apprentissage automatique utilisée pour les tâches de classification basées sur la construction d'un arbre de décision. Cette méthode divise l'ensemble de données en sous-groupes plus petits en effectuant une série de tests conditionnels sur les caractéristiques et détermine la classe d'un objet en fonction du chemin qu'il suit dans l'arbre.
Principes du Classificateur Decision Tree :
- Construction de l'arbre de décision : Au départ, toutes les données sont représentées à la racine de l'arbre. Pour chaque nœud de l'arbre, les données sont divisées en deux sous-groupes ou plus sur la base des valeurs d'une caractéristique, dans le but de minimiser l'incertitude (par exemple, l'entropie ou l'indice de Gini) dans chaque sous-groupe.
- Construction récursive : Le processus de division des données est effectué de manière récursive jusqu'à ce que l'arbre atteigne ses feuilles. Les feuilles représentent les dernières classes d'objets.
- Prise de décision : Lorsqu'un objet entre dans l'arbre, il suit un chemin allant de la racine à l'une des feuilles, où sa classe est déterminée en fonction de la majorité des objets présents dans cette feuille.
Avantages du Classificateur Decision Tree :
- Interprétabilité : Les arbres de décision sont faciles à interpréter et à visualiser. Les règles de décision utilisées pour la classification sont compréhensibles.
- Traitement de différents types de données : Le Classificateur Decision Tree peut travailler avec des caractéristiques numériques et catégorielles.
- Importance de la Fonctionnalité : Les arbres de décision permettent d'évaluer l'importance des caractéristiques, ce qui aide les analystes de données et les ingénieurs à comprendre les données.
Limites du Classificateur Decision Tree :
- Sur-ajustement : Les arbres de grande taille et les arbres profonds peuvent être sujets à un sur-ajustement, ce qui les rend moins généralisables à de nouvelles données.
- Sensibilité au bruit : Les arbres de décision peuvent être sensibles au bruit et aux valeurs aberrantes des données.
- Construction gourmande : Les arbres de décision sont construits à l'aide d'un algorithme gourmand, ce qui peut conduire à des solutions globales sous-optimales.
- Instabilité face aux changements de données : Des modifications mineures des données peuvent entraîner des changements importants dans la structure de l'arbre.
L'arbre de décision est une méthode d'apprentissage automatique utile pour les tâches de classification, en particulier dans les situations où l'interprétabilité du modèle est essentielle et où vous devez comprendre quelles caractéristiques influencent la décision. Cette méthode peut également être utilisée dans des méthodes d'ensemble telles que Random Forest et Gradient Boosting.
2.12.1. Code pour la Création du Modèle de Classification Decision Tree
Ce code démontre le processus d'entraînement d'un modèle de Classification Decision Tree sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_DecisionTreeClassifier.py # The code uses the Decision Tree Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Decision Tree Classifier model decision_tree_model = DecisionTreeClassifier(random_state=42) # train the model on the entire dataset decision_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = decision_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Decision Tree Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(decision_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "decision_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Decision Tree Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Decision Tree Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\decision_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Decision Tree Classifier model in ONNX format: 1.0
Le modèle de Classification Decision Tree (et sa version ONNX) a démontré une précision de 100% dans la classification de l'ensemble des données d'Iris de Fisher.
2.12.2. Code MQL5 pour Travailler avec le Modèle de Classification Decision Tree
//+------------------------------------------------------------------+ //| Iris_DecisionTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "decision_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="DecisionTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_DecisionTreeClassifier (EURUSD,H1) model:DecisionTreeClassifier correct results: 100.00% Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier all samples accuracy=1.000000 Iris_DecisionTreeClassifier (EURUSD,H1) model=DecisionTreeClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 100%, ce qui correspond à la précision du modèle original.
2.12.3. Représentation ONNX du Classificateur Decision Tree
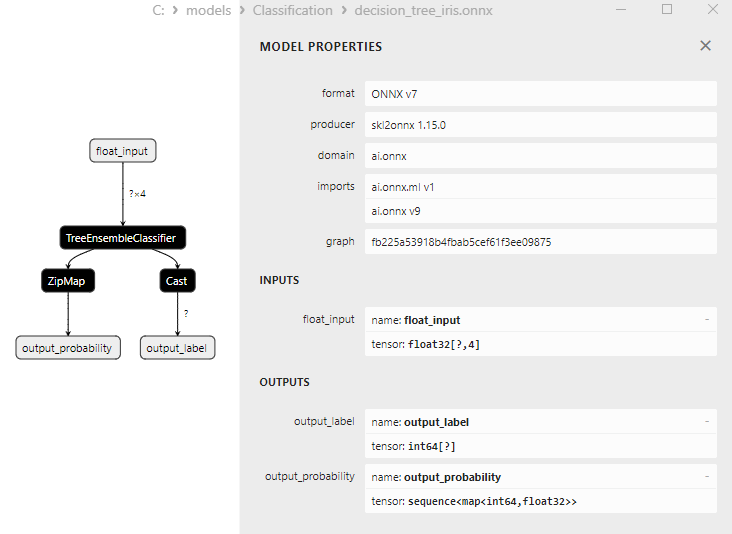
Figure 26. Représentation ONNX du Classificateur Decision Tree dans Netron
Note sur LogisticRegression et LogisticRegressionCV :
LogisticRegression et LogisticRegressionCV sont deux classificateurs utilisés pour la classification binaire à l'aide de la régression logistique, mais ils diffèrent dans la manière dont les paramètres du modèle sont réglés :
LogisticRegression :
- LogisticRegression est un classificateur qui utilise la fonction logistique pour modéliser la probabilité d'appartenir à l'une des deux classes (classification binaire).
- Il fournit des paramètres de base pour la personnalisation, tels que C (force de régularisation inverse), pénalité (type de régularisation, par exemple L1 ou L2), solveur (algorithme d'optimisation), et autres.
- Lorsque vous utilisez la régression logistique, vous choisissez généralement manuellement les valeurs des paramètres et leurs combinaisons, puis vous entraînez le modèle sur les données.
LogisticRegressionCV :
- LogisticRegressionCV est une extension de LogisticRegression qui fournit un support intégré pour la validation croisée et la sélection de la valeur optimale du paramètre de régularisation C.
- Au lieu de sélectionner manuellement C, vous pouvez transmettre à LogisticRegressionCV une liste de valeurs C à explorer et spécifier la méthode de validation croisée (par exemple, à l'aide du paramètre cv).
- LogisticRegressionCV sélectionne automatiquement la valeur C optimale qui donne les meilleurs résultats en validation croisée.
- Ceci est pratique lorsque vous avez besoin d'ajuster automatiquement la régularisation, en particulier si vous avez beaucoup de données ou si vous n'êtes pas sûr de la valeur de C à choisir.
La principale différence entre eux réside donc dans le niveau d'automatisation du réglage des paramètres. LogisticRegression nécessite un réglage manuel de C, alors que LogisticRegressionCV permet la sélection automatique de la valeur optimale de C par validation croisée. Le choix de l'un ou l'autre dépend de vos besoins et de votre désir d'automatiser le processus de mise au point du modèle.
2.13. Classificateur Logistic Regression
Le Classificateur Logistic Regression est une méthode d'apprentissage automatique utilisée pour les tâches de classification binaire et multi-classe. Malgré son nom, "régression", la régression logistique prédit en fait la probabilité qu'un objet appartienne à l'une des classes. La décision finale de classification est prise sur la base de ces probabilités.
Principes du Classificateur Logistic Regression :
- Prédiction de Probabilité : La régression logistique modélise la probabilité qu'un objet appartienne à une classe spécifique en utilisant la fonction logistique (sigmoïde).
- Limite de Décision : Sur la base des probabilités prédites, la régression logistique détermine la limite de décision qui sépare les classes. Si la probabilité dépasse un certain seuil (généralement 0,5), l'objet est classé dans une classe. Dans le cas contraire, il est classé dans une autre classe.
- Apprentissage des Paramètres : Le modèle de régression logistique est formé sur un ensemble de données d'apprentissage en ajustant les poids (coefficients) associés aux caractéristiques afin de minimiser la fonction de perte.
Avantages du Classificateur Logistic Regression :
- Simplicité et Interprétabilité : La régression logistique est un modèle simple dont les résultats sont facilement interprétables en ce qui concerne l'influence des caractéristiques sur les prédictions de classe.
- Efficacité avec les Grands Ensembles de Données : La régression logistique permet de traiter efficacement de grands ensembles de données et de s'y entraîner rapidement.
- Utilisation dans les Méthodes d'Ensemble : La régression logistique peut servir de classificateur de base dans les méthodes d'ensemble telles que l'empilement.
Limites du Classificateur Logistic Regression :
- Linéarité : La régression logistique suppose une relation linéaire entre les caractéristiques et le logarithme des chances, ce qui peut être inadéquat pour des tâches complexes.
- Contrainte Multi-classes : Dans sa forme originale, la régression logistique est conçue pour la classification binaire. Mais il existe des méthodes comme One-vs-All (One-vs-Rest) pour l'étendre à la classification multi-classes.
- Sensibilité aux Valeurs Aberrantes : La régression logistique peut être sensible aux valeurs aberrantes des données.
La régression logistique est une méthode classique d'apprentissage automatique largement utilisée dans la pratique pour les tâches de classification, en particulier lorsque l'interprétabilité du modèle est importante et que les données présentent une structure linéaire ou quasi-linéaire. Il est également utilisé dans les statistiques et l'analyse des données médicales pour évaluer l'impact des facteurs sur la probabilité des événements.
2.13.1. Code pour la Création d'un Modèle de Classification Logistic Regression
Ce code démontre le processus d'entraînement d'un modèle de Classification Logistic Regression sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_LogisticRegressionClassifier.py # The code uses the Logistic Regression Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Logistic Regression Classifier model logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Logistic Regression Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regression_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Logistic Regression Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Logistic Regression Classifier model: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.94 0.96 50
Python 2 0.94 0.98 0.96 50
Python
Python accuracy 0.97 150
Python macro avg 0.97 0.97 0.97 150
Python weighted avg 0.97 0.97 0.97 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Logistic Regression Classifier model in ONNX format: 0.9733333333333334
2.13.2. Code MQL5 pour Travailler avec le Modèle de Classification Regression
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regression_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Sortie :
Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_LogisticRegressionClassifier (EURUSD,H1) model:LogisticRegressionClassifier correct results: 97.33% Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier all samples accuracy=0.973333 Iris_LogisticRegressionClassifier (EURUSD,H1) model=LogisticRegressionClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 97,33%, ce qui correspond à la précision du modèle original.
2.13.3. Représentation ONNX du Classificateur Logistic Regression
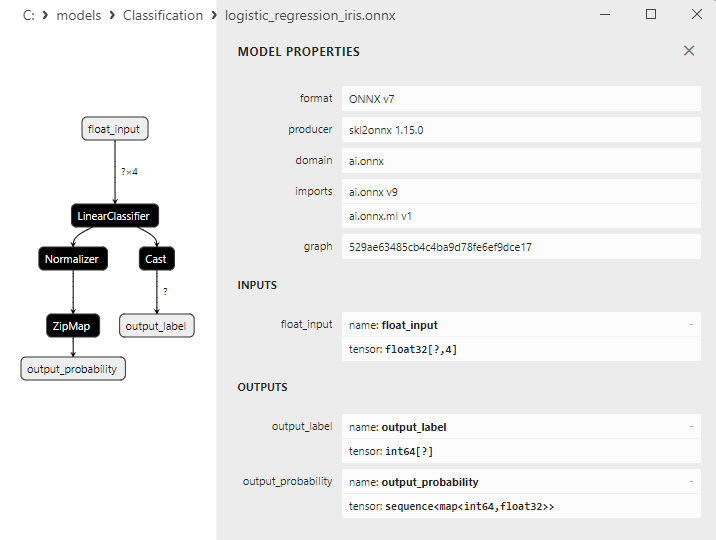
Figure 27. Représentation ONNX du Classificateur Logistic Regression dans Netron
2.14. Classificateur LogisticRegressionCV
LogisticRegressionCV (Logistic Regression with Cross-Validation) est une méthode puissante et flexible de classification binaire. Cette méthode permet non seulement de créer des modèles de classification basés sur la régression logistique, mais aussi d'ajuster automatiquement les paramètres pour obtenir les meilleures performances.
Principes de Travail de LogisticRegressionCV :
- Régression Logistique : LogisticRegressionCV est fondamentalement basé sur la régression logistique. La régression logistique est une méthode statistique utilisée pour modéliser la probabilité qu'un objet appartienne à l'une des deux classes. Ce modèle est appliqué lorsque la variable dépendante est binaire (deux classes) ou peut être transformée en binaire.
- Validation Croisée : Le principal avantage de LogisticRegressionCV est sa validation croisée intégrée. Cela signifie qu'au lieu de sélectionner manuellement la valeur optimale du paramètre de régularisation C, la méthode essaie automatiquement différentes valeurs de C et sélectionne celle qui donne les meilleurs résultats lors de la validation croisée.
- Choisir le C Optimal : LogisticRegressionCV utilise une stratégie de validation croisée pour évaluer les performances du modèle à différentes valeurs de C. C est le paramètre de régularisation qui contrôle l'étendue de la régularisation du modèle. Une petite valeur de C indique une forte régularisation, alors qu'une grande valeur de C indique une faible régularisation. La validation croisée permet de sélectionner la valeur C optimale pour équilibrer l'ajustement insuffisant et l'ajustement excessif.
- Régularisation : LogisticRegressionCV prend également en charge différents types de régularisation, y compris la régularisation L1 (lasso) et L2 (ridge). Ces types de régularisation permettent d'améliorer la généralisation du modèle et d'éviter le sur-ajustement.
Avantages de LogisticRegressionCV :
Réglage Automatique des Paramètres : L'un des principaux avantages de LogisticRegressionCV est sa capacité à choisir automatiquement la valeur C optimale à l'aide de la validation croisée. Cela élimine la nécessité d'ajuster manuellement le modèle et vous permet de vous concentrer sur les données et la tâche.
Robustesse du Sur-Ajustement : La régularisation prise en charge par LogisticRegressionCV permet de contrôler la complexité du modèle et de réduire le risque de sur-ajustement, en particulier avec des données limitées.
Transparence : La régression logistique est une méthode interprétable. Vous pouvez analyser la contribution de chaque caractéristique à la prédiction, ce qui est utile pour comprendre l'importance des caractéristiques.
Haute Performance : La régression logistique permet de travailler rapidement et efficacement, en particulier avec un grand volume de données.
Limites de LogisticRegressionCV :
Dépendances Linéaires : LogisticRegressionCV permet de résoudre les problèmes de classification linéaire et quasi-linéaire. Si la relation entre les caractéristiques et la variable cible est fortement non linéaire, le modèle risque de ne pas donner de bons résultats.
Gestion d'un Grand Nombre de Caractéristiques : Avec un grand nombre de caractéristiques, la régression logistique peut nécessiter des données substantielles ou des techniques de réduction de la dimensionnalité pour éviter le sur-ajustement.
Dépendance de la Représentation des Données : L'efficacité de la régression logistique peut dépendre de la façon dont les données sont représentées et des caractéristiques choisies.
LogisticRegressionCV est un outil puissant pour la classification binaire avec un réglage automatique des paramètres et une robustesse au sur-ajustement. Elle est particulièrement utile lorsqu'il s'agit de construire rapidement un modèle de classification interprétable. Mais il est important de se rappeler qu'elle est plus performante lorsque les données présentent des dépendances linéaires ou quasi-linéaires.
2.14.1. Code de Création du Modèle de Classification LogisticRegressionCV
Ce code démontre le processus d'entraînement d'un modèle de Classification LogisticRegressionCV sur le jeu de données Iris, son export au format ONNX, et l'exécution de la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_LogisticRegressionCVClassifier.py # The code demonstrates the process of training LogisticRegressionCV model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import LogisticRegressionCV from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a LogisticRegressionCV model logistic_regression_model = LogisticRegressionCV(cv=5, max_iter=1000) # train the model on the entire dataset logistic_regression_model.fit(X, y) # predict classes for the entire dataset y_pred = logistic_regression_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of LogisticRegressionCV model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(logistic_regression_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "logistic_regressioncv_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of LogisticRegressionCV model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of LogisticRegressionCV model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\logistic_regression_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of LogisticRegressionCV model in ONNX format: 0.98
2.14.2. Code MQL5 pour Travailler avec le Modèle de Classification LogisticRegressionCV
//+------------------------------------------------------------------+ //| Iris_LogisticRegressionCVClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "logistic_regressioncv_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LogisticRegressionCVClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LogisticRegressionCVClassifier (EURUSD,H1) model:LogisticRegressionCVClassifier correct results: 98.00% Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier all samples accuracy=0.980000 Iris_LogisticRegressionCVClassifier (EURUSD,H1) model=LogisticRegressionCVClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 98%, ce qui correspond à la précision du modèle original.
2.14.3. Représentation ONNX du Classificateur LogisticRegressionCV
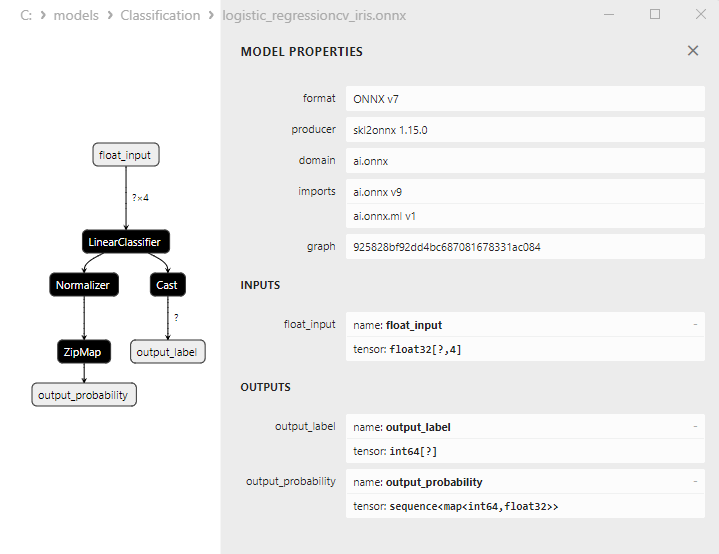
Figure 28. Représentation ONNX du Classificateur LogisticRegressionCV dans Netron
2.15. Classificateur Passif-Agressif (PA)
Le Classificateur Passif-Agressif (PA) est une méthode d'apprentissage automatique utilisée pour les tâches de classification. L'idée centrale de cette méthode est d'adapter les poids (coefficients) du modèle pendant l'apprentissage afin de minimiser les erreurs de classification. Le Classificateur Passif-Agressif peut être utile dans les scénarios d'apprentissage en ligne et dans les situations où les données changent au fil du temps.
Principes de Fonctionnement du Classificateur Passif-Agressif :
- Adaptation des Poids : Au lieu de mettre à jour les poids du modèle dans le sens de la minimisation de la fonction de perte, comme c'est le cas dans la descente de gradient stochastique, le Classificateur Passif-Agressif adapte les poids dans le sens de la minimisation de l'erreur de classification pour l'exemple en cours.
- Maintien de l'Agressivité : La méthode dispose d'un paramètre appelé agressivité (C), qui détermine l'intensité avec laquelle les poids du modèle doivent être adaptés. Des valeurs de C plus élevées rendent la méthode plus agressive dans l'adaptation, alors que des valeurs plus petites la rendent moins agressive.
Avantages du Classificateur Passif-Agressif :
- Adapté à l'Apprentissage en Ligne : Le Classificateur Passif-Agressif peut être mis à jour au fur et à mesure de l'arrivée de nouvelles données, ce qui le rend adapté aux tâches d'apprentissage en ligne où les données arrivent en flux continu.
- Adaptabilité aux Changements de Données : La méthode fonctionne bien avec des données changeantes puisqu'elle adapte le modèle aux nouvelles circonstances.
Limites du Classificateur Passif-Agressif :
- Sensibilité au Choix du Paramètre d'Agressivité : La sélection de la valeur optimale du paramètre d'agressivité C peut nécessiter un réglage et dépend des caractéristiques des données.
- N'est pas toujours adapté aux tâches complexes : Le Classificateur Passif-Agressif peut ne pas offrir une grande précision dans les tâches complexes où des dépendances complexes doivent être prises en compte.
- Interprétation des Poids : Les poids des modèles obtenus à l'aide de cette méthode peuvent être moins faciles à interpréter que les poids obtenus à l'aide d'une régression linéaire ou logistique.
Le Classificateur Passif-Agressif est une méthode d'apprentissage automatique adaptée aux tâches de classification avec des données évolutives et aux situations où l'adaptation rapide du modèle à de nouvelles circonstances est cruciale. Il trouve des applications dans divers domaines, notamment l'analyse de données textuelles, la classification d'images et d'autres tâches.
2.15.1. Code pour la Création du Modèle de Classificateur Passif-Agressif (PA)
Ce code démontre le processus d'entraînement d'un modèle de Classificateur Passif-Agressif (PA) sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_PassiveAgressiveClassifier.py # The code uses the Passive-Aggressive (PA) Classifier for the Iris dataset, converts the model to ONNX format, saves it, and evaluates its accuracy. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import PassiveAggressiveClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Passive-Aggressive (PA) Classifier model pa_classifier_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset pa_classifier_model.fit(X, y) # predict classes for the entire dataset y_pred = pa_classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Passive-Aggressive (PA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(pa_classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "pa_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Passive-Aggressive (PA) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Passive-Aggressive (PA) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.96 0.92 0.94 50
Python 2 0.92 0.96 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\pa_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Passive-Aggressive (PA) Classifier model in ONNX format: 0.96
2.15.2. Code MQL5 pour Travailler avec le Modèle de Classification Passif-Agressif (PA)
//+------------------------------------------------------------------+ //| Iris_PassiveAgressiveClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "pa_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PassiveAgressiveClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PassiveAgressiveClassifier (EURUSD,H1) model:PassiveAgressiveClassifier correct results: 96.00% Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier all samples accuracy=0.960000 Iris_PassiveAgressiveClassifier (EURUSD,H1) model=PassiveAgressiveClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 96%, ce qui correspond à la précision du modèle original.
2.15.3. Représentation ONNX du Classificateur Passif-Agressif (PA)
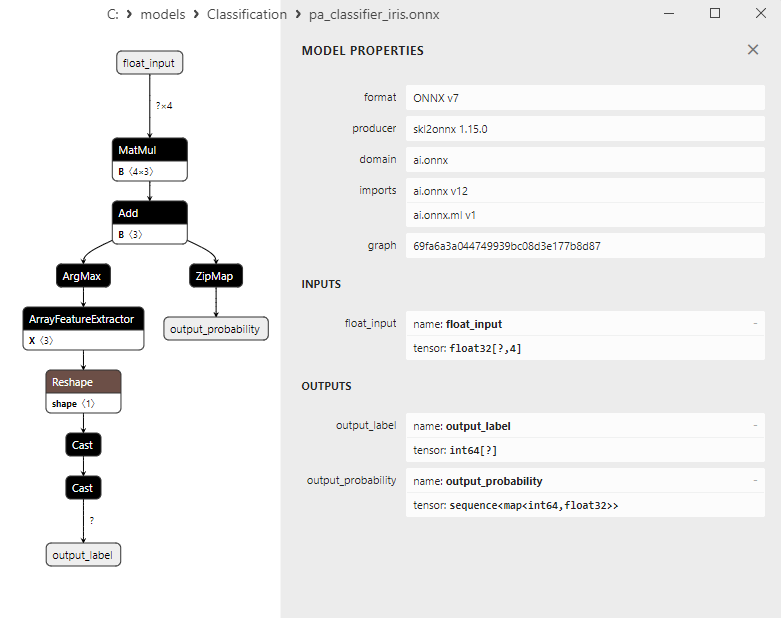
Figure 29. Représentation ONNX du Classificateur Passif-Agressif (PA) dans Netron
2.16. Classificateur Perceptron
Le Classificateur Perceptron est un classificateur binaire linéaire utilisé pour séparer deux classes sur la base d'un hyperplan de séparation linéaire. Il s'agit de l'une des méthodes d'apprentissage automatique les plus simples et les plus anciennes, dont le principe de base consiste à former les poids (coefficients) du modèle afin de maximiser la précision de la classification sur l'ensemble des données d'apprentissage.
Principes de Fonctionnement du Classificateur Perceptron :
- Hyper-plan linéaire : Le Perceptron construit un hyper-plan linéaire dans l'espace des caractéristiques qui sépare deux classes. Cet hyper-plan est déterminé par les poids (coefficients) du modèle.
- Entraînement des Poids : Au départ, les poids sont initialisés de manière aléatoire ou à zéro. Pour chaque objet de l'ensemble de données d'apprentissage, le modèle prédit ensuite la classe sur la base des poids actuels et les ajuste en cas d'erreur. L'apprentissage se poursuit jusqu'à ce que tous les objets soient classés correctement ou jusqu'à ce qu'un nombre maximal d'itérations soit atteint.
Avantages du Classificateur Perceptron :
- Simplicité : Le Perceptron est un algorithme très simple, facile à comprendre et à mettre en œuvre.
- Vitesse d'Entraînement Elevée : Le Perceptron peut être formé rapidement, en particulier sur de grands ensembles de données, et peut être utilisé dans des tâches d'apprentissage en ligne.
Limites du Classificateur Perceptron :
- Contrainte de Séparabilité Linéaire : Le Perceptron ne fonctionne bien que dans les cas où les données sont linéairement séparables. Si les données ne peuvent pas être séparées linéairement, le Perceptron risque de ne pas atteindre une grande précision.
- Sensibilité aux Poids Initiaux : Le choix initial des poids peut avoir un impact sur la convergence de l'algorithme. De mauvais choix de poids initiaux peuvent conduire à une convergence lente ou à un neurone qui ne peut pas séparer correctement les classes.
- Incapacité à Déterminer les Probabilités : Le Perceptron ne fournit pas d'estimation de la probabilité d'appartenance à une classe, ce qui peut être important pour certaines tâches.
Le Classificateur Perceptron est un algorithme de base pour la classification binaire qui peut être utile dans les cas simples où les données sont linéairement séparables. Il peut également servir de base à des méthodes plus complexes, telles que les réseaux neuronaux multicouches. Il est important de se rappeler que dans les tâches plus complexes où les données ont des structures complexes, d'autres méthodes comme la régression logistique ou les Machines à Vecteurs de Support (SVM) peuvent fournir une meilleure précision de classification.
2.16.1. Code de Création du Modèle de Classification Perceptron
Ce code démontre le processus d'entraînement d'un modèle de Classification Perceptron sur le jeu de données Iris, son export au format ONNX, et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_PerceptronClassifier.py # The code demonstrates the process of training Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import Perceptron from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Perceptron Classifier model perceptron_model = Perceptron(max_iter=1000, random_state=42) # train the model on the entire dataset perceptron_model.fit(X, y) # predict classes for the entire dataset y_pred = perceptron_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Perceptron Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(perceptron_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "perceptron_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Perceptron Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Perceptron Classifier model: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 0.80 0.89 50
Python 1 0.46 1.00 0.63 50
Python 2 1.00 0.04 0.08 50
Python
Python accuracy 0.61 150
Python macro avg 0.82 0.61 0.53 150
Python weighted avg 0.82 0.61 0.53 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Perceptron Classifier model in ONNX format: 0.6133333333333333
2.16.2. Code MQL5 pour Travailler avec le Modèle de Classification Perceptron
//+------------------------------------------------------------------+ //| Iris_PerceptronClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "perceptron_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="PerceptronClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier correct results: 61.33% Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier all samples accuracy=0.613333 Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10) Iris_PerceptronClassifier (EURUSD,H1) model:PerceptronClassifier FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80) Iris_PerceptronClassifier (EURUSD,H1) model=PerceptronClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 61,33%, ce qui correspond à la précision du modèle original.
2.16.3. Représentation ONNX du Classificateur Perceptron
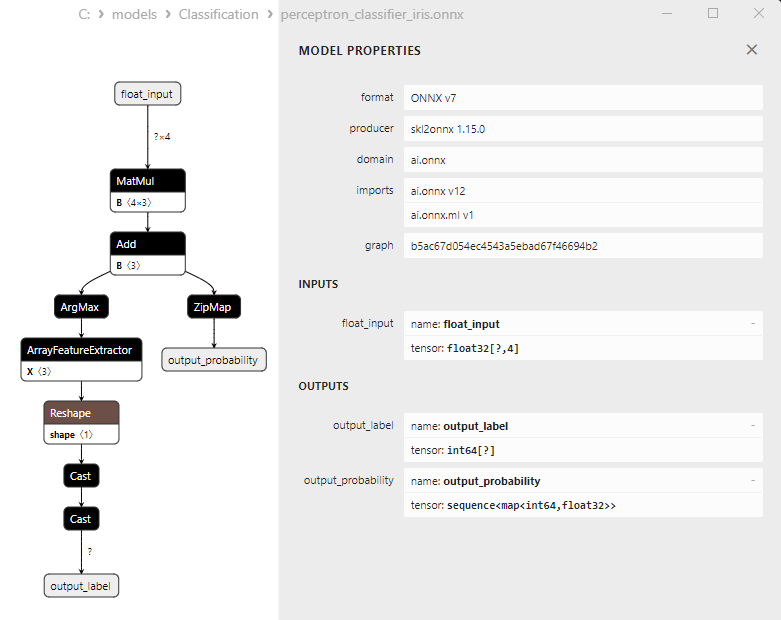
Figure 30. Représentation ONNX du Classificateur Perceptron dans Netron
2.17. Classificateur Stochastic Gradient Descent
Le Classificateur SGD (Stochastic Gradient Descent) est une méthode d'apprentissage automatique utilisée pour les tâches de classification. Il s'agit d'un cas spécifique de modèles linéaires et d'un classificateur linéaire formé à l'aide d'une descente de gradient stochastique.
Principes du Classificateur SGD :
- Hyper-plan linéaire : Le Classificateur SGD construit un hyper-plan linéaire dans l'espace multidimensionnel des caractéristiques qui sépare 2 classes. Cet hyper-plan est déterminé par les poids (coefficients) du modèle.
- Descente Stochastique de Gradient : La méthode est entraînée à l'aide de la descente de gradient stochastique, ce qui signifie que les mises à jour des poids sont effectuées sur chaque objet de l'ensemble de données d'entraînement (ou d'un sous-ensemble sélectionné de manière aléatoire), plutôt que sur l'ensemble de données complet. Le Classificateur SGD est donc adapté aux grands volumes de données et à l'apprentissage en ligne.
- Fonction de Perte : Le Classificateur SGD optimise une fonction de perte, telle que la fonction de perte logistique pour la classification binaire ou la fonction de perte softmax pour la classification multi-classes.
Avantages du Classificateur SGD :
- Vitesse d'Entraînement : Le Classificateur SGD s'entraîne rapidement, en particulier sur de grands volumes de données, grâce à la descente de gradient stochastique.
- Adapté à l'Apprentissage en Ligne : La méthode est bien adaptée aux tâches d'apprentissage en ligne où les données arrivent en flux continu et où le modèle doit être mis à jour au fur et à mesure de l'arrivée de nouvelles données.
Limites du Classificateur SGD :
- Sensibilité aux Paramètres : Le Classificateur SGD possède de nombreux hyper-paramètres, tels que le taux d'apprentissage et le paramètre de régularisation, qui nécessitent un réglage minutieux.
- Initialisation des Poids : Le choix initial des poids peut influencer la convergence et la qualité du modèle.
- Convergence Vers les Minima Locaux : En raison de la nature stochastique de la méthode SGD, elle peut converger vers des minima locaux de la fonction de perte, ce qui peut affecter la qualité du modèle.
Le Classificateur SGD est une méthode d'apprentissage automatique polyvalente qui peut être utilisée pour les tâches de classification binaire et multi-classes, en particulier lorsqu'il s'agit de traiter de grands volumes de données nécessitant un traitement rapide. Il est important d'ajuster correctement ses hyper-paramètres et de surveiller la convergence afin d'obtenir une précision de classification élevée.
2.17.1. Code de Création du Modèle de Classification Stochastic Gradient Descent
Ce code démontre le processus d'entraînement d'un modèle de Classificateur SGD sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_SGDClassifier.py # The code demonstrates the process of training Stochastic Gradient Descent Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.linear_model import SGDClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an SGD Classifier model sgd_model = SGDClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset sgd_model.fit(X, y) # predict classes for the entire dataset y_pred = sgd_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of SGD Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(sgd_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "sgd_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of SGD Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of SGD Classifier model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.88 0.92 0.90 50
Python 2 0.96 0.88 0.92 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\perceptron_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of SGD Classifier model in ONNX format: 0.9333333333333333
2.17.2. Code MQL5 pour Travailler avec le Modèle de Classification Stochastic Gradient Descent
//+------------------------------------------------------------------+ //| Iris_SGDClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "sgd_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="SGDClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier correct results: 93.33% Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier all samples accuracy=0.933333 Iris_SGDClassifier (EURUSD,H1) model:SGDClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_SGDClassifier (EURUSD,H1) model=SGDClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 93,33%, ce qui correspond à la précision du modèle original.
2.17.3. Représentation ONNX du Classificateur Stochastic Gradient Descent
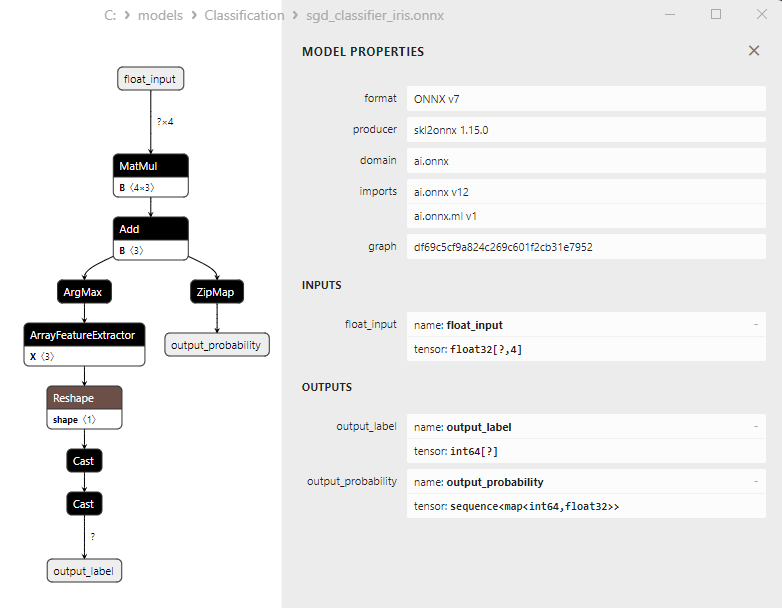
Figure 31. Représentation ONNX du Classificateur Stochastic Gradient Descent dans Netron
2.18. Classificateur Gaussian Naive Bayes (GNB)
Le Classificateur Gaussian Naive Bayes (GNB) est une méthode d'apprentissage automatique basée sur un modèle probabiliste bayésien utilisé pour les tâches de classification. Il fait partie de la famille des classificateurs naïfs de Bayes et suppose que toutes les caractéristiques sont indépendantes et ont une distribution normale.
Principes du Classificateur Gaussian Naive Bayes :
- Approche Bayésienne : Le GNB est basé sur l'approche bayésienne de la classification, qui utilise le théorème de Bayes pour calculer la probabilité d'appartenance d'un objet à chaque classe.
- Hypothèse Naïve : L'hypothèse clé du GNB est que toutes les caractéristiques sont indépendantes et suivent une distribution normale (gaussienne). Cette hypothèse est considérée comme naïve car, dans les données réelles, les caractéristiques sont souvent en corrélation les unes avec les autres.
- Estimation des Paramètres : Le modèle GNB est entraîné sur l'ensemble des données d'entraînement en calculant les paramètres de la distribution (moyenne et écart-type) pour chaque caractéristique de chaque classe.
Avantages du Classificateur Gaussian Naive Bayes :
- Simplicité et Rapidité de Formation : Le GNB est un algorithme très simple qui s'entraîne rapidement, même sur de grands ensembles de données.
- Efficacité pour les Petites et Moyennes Données : Le GNB peut être efficace pour les tâches de classification comportant un nombre faible ou moyen de caractéristiques, en particulier lorsque l'hypothèse d'une distribution normale des caractéristiques est respectée.
Limites du Classificateur Gaussian Naive Bayes :
- Hypothèse Naïve : L'hypothèse de l'indépendance des caractéristiques et de la distribution normale peut être trop simpliste et incorrecte pour les données du monde réel, ce qui réduit la précision de la classification.
- Sensibilité aux Valeurs Aberrantes : Le GNB peut être sensible aux valeurs aberrantes dans les données car elles peuvent fausser de manière significative les paramètres de la distribution normale.
- Incapacité à Saisir les Dépendances des Caractéristiques : En raison de l'hypothèse d'indépendance, le GNB ne tient pas compte des dépendances entre les caractéristiques.
Le Classificateur Gaussian Naive Bayes est un bon choix pour les tâches de classification simples, en particulier lorsque l'hypothèse de distribution normale des caractéristiques est approximativement respectée. Mais dans les tâches plus complexes où les caractéristiques sont corrélées ou ne suivent pas une distribution normale, d'autres méthodes telles que les Machines à Vecteurs de Support (SVM) ou le gradient boosting peuvent fournir des résultats plus précis.
2.18.1. Code de Création du Modèle de Classification Gaussian Naive Bayes (GNB)
Ce code démontre le processus d'entraînement d'un modèle de Classificateur Gaussian Naive Bayes (GNB) sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_GaussianNaiveBayesClassifier.py # The code demonstrates the process of training Gaussian Naive Bayes Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import GaussianNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Gaussian Naive Bayes (GNB) Classifier model gnb_model = GaussianNB() # train the model on the entire dataset gnb_model.fit(X, y) # predict classes for the entire dataset y_pred = gnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Gaussian Naive Bayes (GNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(gnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "gnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.94 0.94 50
Python 2 0.94 0.94 0.94 50
Python
Python accuracy 0.96 150
Python macro avg 0.96 0.96 0.96 150
Python weighted avg 0.96 0.96 0.96 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\gnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Gaussian Naive Bayes (GNB) Classifier model in ONNX format: 0.96
2.18.2. Code MQL5 pour Travailler avec le Modèle de Classificateur Gaussian Naive Bayes (GNB)
//+------------------------------------------------------------------+ //| Iris_GaussianNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "gnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="GaussianNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model:GaussianNaiveBayesClassifier correct results: 96.00% Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier all samples accuracy=0.960000 Iris_GaussianNaiveBayesClassifier (EURUSD,H1) model=GaussianNaiveBayesClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 96%, ce qui correspond à la précision du modèle original.
2.18.3. Représentation ONNX du Classificateur Gaussian Naive Bayes (GNB)
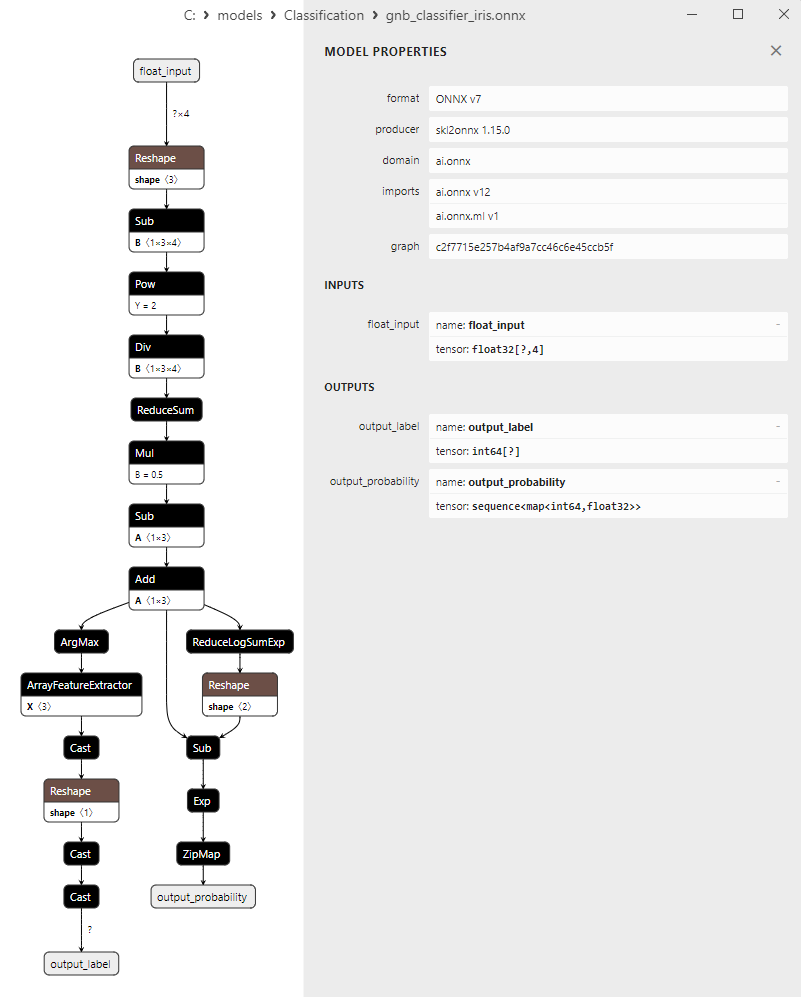
Figure 32. Représentation ONNX du Classificateur Gaussian Naive Bayes (GNB) dans Netron
2.19. Classificateur Multinomial Naive Bayes (MNB)
Le Classificateur Multinomial Naive Bayes (MNB) est une méthode d'apprentissage automatique basée sur un modèle probabiliste bayésien et est utilisé pour les tâches de classification, en particulier dans le traitement de texte. Il s'agit de l'une des variantes des classificateurs de Bayes naïfs, qui partent du principe que les caractéristiques représentent des nombres, tels que le nombre d'occurrences de mots dans un texte.
Principes du Classificateur Multinomial Naive Bayes :
- Approche Bayésienne : MNB suit également l'approche bayésienne de la classification, en utilisant le théorème de Bayes pour calculer la probabilité qu'un objet appartienne à chaque classe.
- Hypothèse d'une Distribution Multinomiale : L'hypothèse principale de MNB est que les caractéristiques représentent des nombres, tels que le nombre d'occurrences de mots dans un texte, et qu'elles suivent une distribution multinomiale. Cette hypothèse est souvent valable pour les données textuelles.
- Estimation des Paramètres : Le modèle MNB est formé sur l'ensemble des données d'apprentissage en calculant les paramètres de la distribution pour chaque caractéristique au sein de chaque classe.
Avantages du Classificateur Multinomial Naive Bayes :
- Efficacité dans le Traitement du Texte : MNB donne de bons résultats dans les tâches liées à l'analyse de données textuelles, telles que la classification de textes ou le filtrage de spams, grâce à l'hypothèse du nombre de caractéristiques.
- Simplicité et Rapidité de Formation : Comme les autres classificateurs de Bayes naïfs, MNB est un algorithme simple qui s'entraîne rapidement, même sur de grands volumes de données textuelles.
Limites du Classificateur Multinomial Naive Bayes :
- Hypothèse Naïve : L'hypothèse d'une distribution multinomiale des caractéristiques peut être trop simpliste et inexacte pour les données réelles, en particulier lorsque les caractéristiques ont des structures complexes.
- Incapacité à Tenir Compte de l'Ordre des Mots : MNB ne tient pas compte de l'ordre des mots dans le texte, ce qui peut être important dans certaines tâches d'analyse de texte.
- Sensibilité aux Mots Rares : MNB peut être sensible aux mots rares, et un nombre insuffisant d'occurrences peut réduire la précision de la classification.
Le Classificateur Multinomial Naive Bayes est une méthode utile pour les tâches d'analyse de texte, en particulier lorsque les caractéristiques sont liées au nombre, comme le nombre de mots dans le texte. Il est largement utilisé dans le traitement du langage naturel (NLP) pour la classification des textes, la catégorisation des documents et d'autres analyses de texte.
2.19.1. Code de Création du Modèle de Classificateur Multinomial Naive Bayes (MNB)
Ce code démontre le processus d'entraînement d'un modèle de Classificateur Multinomial Naive Bayes (MNB) sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_MultinomialNaiveBayesClassifier.py # The code demonstrates the process of training Multinomial Naive Bayes (MNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import MultinomialNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multinomial Naive Bayes (MNB) Classifier model mnb_model = MultinomialNB() # train the model on the entire dataset mnb_model.fit(X, y) # predict classes for the entire dataset y_pred = mnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multinomial Naive Bayes (MNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "mnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.94 0.92 0.93 50
Python 2 0.92 0.94 0.93 50
Python
Python accuracy 0.95 150
Python macro avg 0.95 0.95 0.95 150
Python weighted avg 0.95 0.95 0.95 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multinomial Naive Bayes (MNB) Classifier model in ONNX format: 0.9533333333333334
2.19.2. Code MQL5 pour Travailler avec le Modèle de Classificateur Multinomial Naive Bayes (MNB)
//+------------------------------------------------------------------+ //| Iris_MultinomialNaiveBayesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MultinomialNaiveBayesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier correct results: 95.33% Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier all samples accuracy=0.953333 Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model:MultinomialNaiveBayesClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MultinomialNaiveBayesClassifier (EURUSD,H1) model=MultinomialNaiveBayesClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 95,33%, ce qui correspond à la précision du modèle original.
2.19.3. Représentation ONNX du Classificateur Multinomial Naive Bayes (MNB)
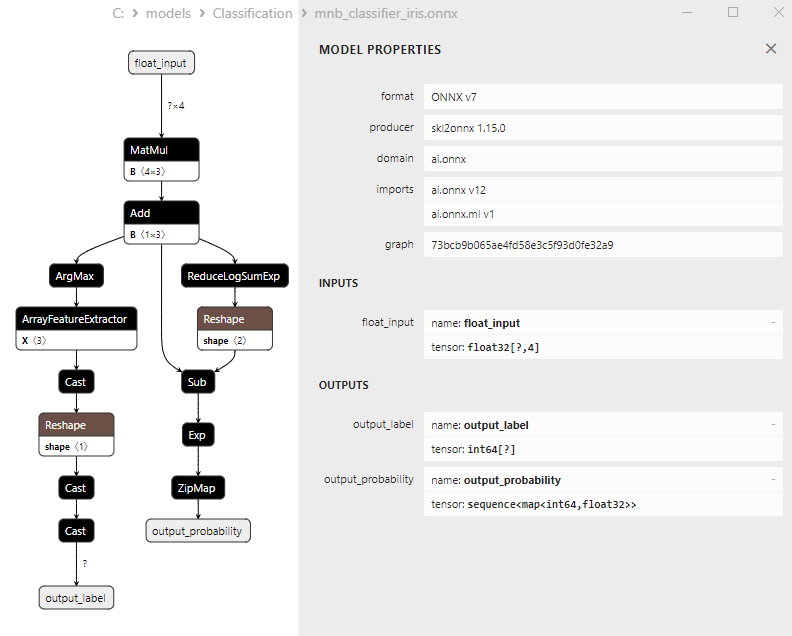
Figure 33. Représentation ONNX du Classificateur Multinomial Naive Bayes (MNB) dans Netron
2.20. Classificateur Complement Naive Bayes (CNB)
Le Classificateur Complement Naive Bayes (CNB) est une variante du Classificateur Naive Bayes qui a été spécialement conçue pour fonctionner avec des données déséquilibrées, où une classe peut être significativement plus répandue que l'autre. Ce classificateur adapte la méthode classique des Bayes naïfs pour traiter le déséquilibre des classes.
Principes du Classificateur Complement Naive Bayes :
- Approche Bayésienne : Comme les autres classificateurs bayésiens, le CNB suit l'approche bayésienne de la classification et utilise le théorème de Bayes pour calculer la probabilité qu'un objet appartienne à chaque classe.
- Remédier au Déséquilibre des Classes : L'objectif premier du CNB est de corriger le déséquilibre des classes. Au lieu de prendre en compte la probabilité des caractéristiques de la classe, comme le fait la méthode standard de Bayes naïf, CNB tente de prendre en compte la probabilité des caractéristiques extérieures à la classe. Cela est particulièrement utile lorsqu'une classe est nettement moins représentée que l'autre.
- Estimation des Paramètres : Le modèle CNB est formé sur l'ensemble des données d'apprentissage en calculant les paramètres de la distribution pour chaque caractéristique en dehors de la classe.
Avantages du Classificateur Complement Naive Bayes :
- Adaptation aux Données Déséquilibrées : Le CNB donne de bons résultats dans les tâches de classification avec des données déséquilibrées, où les classes ont des fréquences différentes.
- Simplicité et Rapidité de Formation : Comme les autres classificateurs de Bayes naïfs, CNB est un algorithme simple qui s'entraîne rapidement, même sur de grands volumes de données.
Limites du Classificateur Complement Naive Bayes :
- Sensibilité au Choix du Paramètre de Régularisation : Comme dans d'autres méthodes bayésiennes, la sélection de la bonne valeur pour le paramètre de régularisation peut nécessiter un réglage et une évaluation.
- Hypothèse Naïve : Comme les autres classificateurs de Bayes naïfs, le CNB suppose l'indépendance des caractéristiques, ce qui peut s'avérer trop simpliste pour certaines tâches.
Le Classificateur Complement Naive Bayes est un bon choix pour les tâches de classification avec des données déséquilibrées, en particulier lorsqu'une classe est nettement moins représentée que l'autre. Elle peut être particulièrement utile dans les tâches de classification de textes où les mots peuvent être fortement déséquilibrés entre les classes, comme l'analyse des sentiments ou le filtrage des spams.
2.20.1. Code pour la Création du Modèle de Classification Complement Naive Bayes (CNB)
Ce code démontre le processus d'entraînement d'un modèle de Classificateur Complement Naive Bayes (CNB) sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_CNBClassifier.py # The code demonstrates the process of training Complement Naive Bayes (CNB) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import ComplementNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Complement Naive Bayes (CNB) Classifier model cnb_model = ComplementNB() # train the model on the entire dataset cnb_model.fit(X, y) # predict classes for the entire dataset y_pred = cnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Complement Naive Bayes (CNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(cnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "cnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Complement Naive Bayes (CNB) Classifier model: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.96 1.00 0.98 50
Python 1 0.00 0.00 0.00 50
Python 2 0.51 1.00 0.68 50
Python
Python accuracy 0.67 150
Python macro avg 0.49 0.67 0.55 150
Python weighted avg 0.49 0.67 0.55 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\cnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Complement Naive Bayes (CNB) Classifier model in ONNX format: 0.6666666666666666
2.20.2. Code MQL5 pour Travailler avec le Modèle de Classificateur Complement Naive Bayes (CNB)
//+------------------------------------------------------------------+ //| Iris_CNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "cnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier correct results: 66.67% Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier all samples accuracy=0.666667 Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40) Iris_CNBClassifier (EURUSD,H1) model:CNBClassifier FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50) Iris_CNBClassifier (EURUSD,H1) model=CNBClassifier batch test accuracy=0.000000La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 66,67%, ce qui correspond à la précision du modèle original.
2.20.3. Représentation ONNX du Classificateur Complement Naive Bayes (CNB)
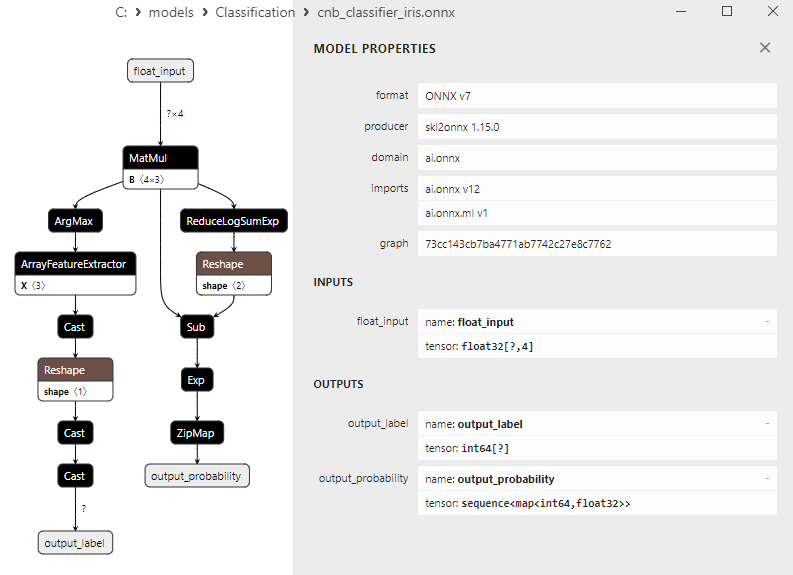
Figure 34. Représentation ONNX du Classificateur Complement Naive Bayes (CNB) dans Netron
2.21. Classificateur Bernoulli Naive Bayes (BNB)
Le Classificateur Bernoulli Naive Bayes (BNB) est une autre variante du classificateur naïf Bayes utilisé pour les tâches de classification binaire. Ce classificateur est particulièrement utile dans les situations où les caractéristiques sont représentées sous forme de données binaires, comme dans l'analyse de texte où les caractéristiques peuvent être la présence ou l'absence de mots dans le texte.
Principes du Classificateur Bernoulli Naive Bayes :
- Approche Bayésienne : Comme les autres classificateurs bayésiens, BNB suit l'approche bayésienne de la classification et utilise le théorème de Bayes pour calculer la probabilité qu'un objet appartienne à chaque classe.
- Hypothèse de Caractéristiques Binaires : L'hypothèse principale de BNB est que les caractéristiques sont représentées comme des données binaires, ce qui signifie qu'elles ne peuvent avoir que deux valeurs, telles que 1 et 0, où 1 représente la présence de la caractéristique et 0 son absence.
- Estimation des Paramètres : Le modèle BNB est formé sur l'ensemble des données d'apprentissage en calculant les paramètres de la distribution pour chaque caractéristique dans chaque classe.
Avantages du Classificateur Bernoulli Naive Bayes :
- Efficacité pour les Données Binaires : Le BNB fonctionne bien dans les tâches où les caractéristiques sont représentées sous forme de données binaires, et il peut être particulièrement utile dans l'analyse de texte ou la classification d'événements.
- Simplicité et Rapidité de Formation : Comme les autres classificateurs de Bayes naïfs, BNB est un algorithme simple qui s'entraîne rapidement.
Limites du Classificateur Bernoulli Naive Bayes :
- Restriction aux Caractéristiques Binaires : Le BNB n'est pas adapté aux tâches pour lesquelles les caractéristiques ne sont pas binaires. Si les caractéristiques ont plus de deux valeurs, BNB ne tient pas compte de cette information.
- Hypothèse Naïve : Comme d'autres classificateurs de Bayes naïfs, BNB suppose l'indépendance des caractéristiques, ce qui peut s'avérer trop simpliste pour certaines tâches.
Le Classificateur Bernoulli Naive Bayes est un bon choix pour les tâches de classification binaire avec des caractéristiques binaires, telles que l'analyse des sentiments dans un texte ou la classification des spams. Il est facile à utiliser et donne de bons résultats avec ce type de données.
2.21.1. Code de Création du Modèle de Classification Bernoulli Naive Bayes (BNB)
Ce code démontre le processus d'entraînement d'un modèle de Classificateur Bernoulli Naive Bayes (BNB) sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_BNBClassifier.py # The code demonstrates the process of training Bernoulli Naive Bayes (BNB) Classifier on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import BernoulliNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Bernoulli Naive Bayes (BNB) Classifier model bnb_model = BernoulliNB() # train the model on the entire dataset bnb_model.fit(X, y) # predict classes for the entire dataset y_pred = bnb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Bernoulli Naive Bayes (BNB) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(bnb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "bnb_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\bnb_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Bernoulli Naive Bayes (BNB) Classifier model in ONNX format: 0.3333333333333333
2.21.2. Code MQL5 pour Travailler avec le Modèle de Classification Bernoulli Naive Bayes (BNB)
//+------------------------------------------------------------------+ //| Iris_BNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "bnb_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="BNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier correct results: 33.33% Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier all samples accuracy=0.333333 Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10) Iris_BNBClassifier (EURUSD,H1) model:BNBClassifier FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80) Iris_BNBClassifier (EURUSD,H1) model=BNBClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 33,33%, ce qui correspond à la précision du modèle original.
2.21.3. Représentation ONNX du Classificateur Bernoulli Naive Bayes (BNB)
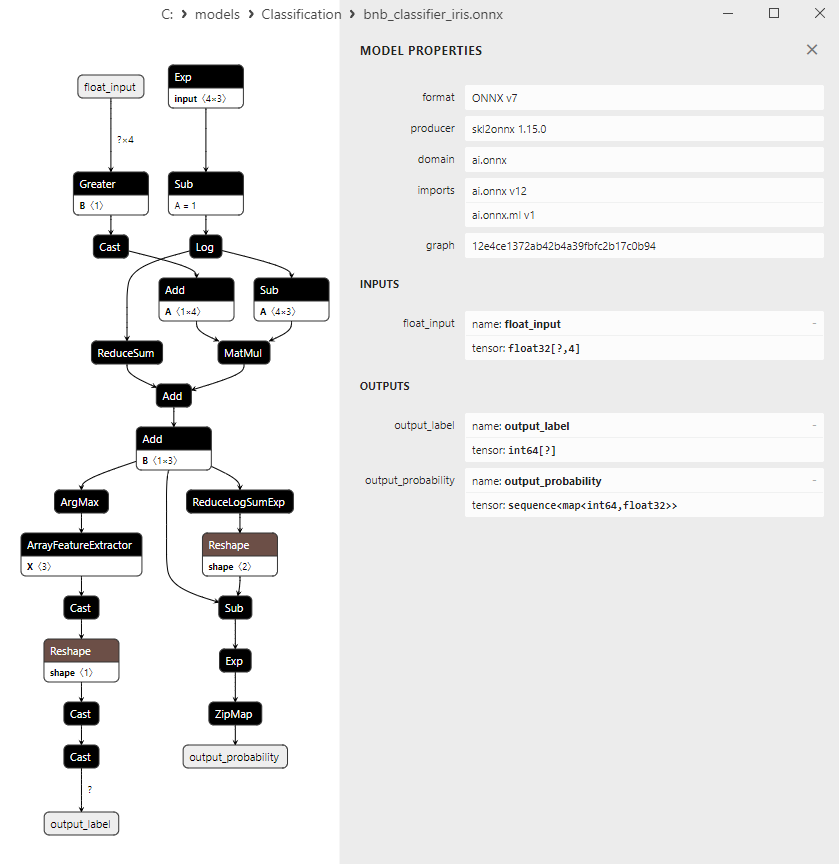
Figure 35. Représentation ONNX du Classificateur Bernoulli Naive Bayes (BNB) dans Netron
2.22. Classificateur Perceptron Multi-couche
Le Classificateur Perceptron Multi-couche (MLP) est un réseau neuronal multicouche utilisé pour les tâches de classification. Il se compose de plusieurs couches de neurones, dont une couche d'entrée, des couches cachées et une couche de sortie. Le Classificateur MLP a la capacité d'apprendre des dépendances non linéaires complexes dans les données.
Principes du Classificateur MLP :
- Architecture Multi-Couche : Le Classificateur MLP a une architecture multi-couche qui comprend une couche d'entrée, une ou plusieurs couches cachées et une couche de sortie. Chaque neurone des couches est connecté aux neurones des couches voisines avec des poids qui sont appris.
- Fonctions d'Activation : À l'intérieur de chaque neurone, une fonction d'activation est appliquée, ce qui introduit une non-linéarité dans le modèle et permet au Classificateur MLP de modéliser des dépendances de données complexes.
- Formation par Rétro-Propagation : Le Classificateur MLP est entraîné à l'aide de la méthode de rétro-propagation, qui minimise l'erreur entre les prédictions du modèle et les véritables étiquettes de classe.
Avantages du Classificateur MLP :
- Capacité à Modéliser des Dépendances Complexes : Le Classificateur MLP peut apprendre des dépendances non linéaires complexes dans les données et, par conséquent, peut donner de bons résultats dans des tâches où les modèles linéaires simples sont insuffisants.
- Polyvalence : Le Classificateur MLP peut être utilisé pour un large éventail de tâches de classification, y compris la classification multi-classes et les problèmes multi-tâches.
Limites du Classificateur MLP :
- Sensibilité aux Hyper-paramètres : Le Classificateur MLP possède de nombreux hyper-paramètres, tels que le nombre de couches cachées, le nombre de neurones dans chaque couche, le taux d'apprentissage, etc. Le réglage de ces paramètres peut prendre beaucoup de temps et nécessiter de nombreuses ressources.
- Exigence de Grandes Quantités de Données : Le Classificateur MLP nécessite une quantité substantielle de données d'apprentissage pour éviter un sur-ajustement, en particulier lorsque le modèle comporte de nombreux paramètres.
- Sur-ajustement : Si le modèle a trop de paramètres ou des données insuffisantes, il peut se sur-adapter et donner de mauvais résultats avec de nouvelles données.
Le Classificateur MLP est un outil puissant pour les tâches de classification, en particulier lorsque les données présentent des dépendances complexes. Il est couramment utilisé dans les domaines de l'apprentissage automatique et de l'apprentissage profond pour résoudre divers problèmes de classification. Toutefois, il est essentiel de régler correctement les hyper-paramètres et de disposer d'une quantité suffisante de données d'apprentissage pour que l'application de ce modèle soit couronnée de succès.
2.22.1. Code pour la Création du Modèle de Classification Perceptron Multi-couche
Ce code démontre le processus d'entraînement d'un Classificateur Perceptron Multicouche sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_MLPClassifier.py # The code demonstrates the process of training Multilayer Perceptron Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.neural_network import MLPClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Multilayer Perceptron (MLP) Classifier model mlp_model = MLPClassifier(max_iter=1000, random_state=42) # train the model on the entire dataset mlp_model.fit(X, y) # predict classes for the entire dataset y_pred = mlp_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Multilayer Perceptron (MLP) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(mlp_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"mlp_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Multilayer Perceptron (MLP) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 0.94 0.97 50
Python 2 0.94 1.00 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\mlp_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Multilayer Perceptron (MLP) Classifier model in ONNX format: 0.98
2.22.2. Code MQL5 pour Travailler avec le Modèle de Classification Perceptron Multi-couche
//+------------------------------------------------------------------+ //| Iris_MLPClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "mlp_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="MLPClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier correct results: 98.00% Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier all samples accuracy=0.980000 Iris_MLPClassifier (EURUSD,H1) model:MLPClassifier FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50) Iris_MLPClassifier (EURUSD,H1) model=MLPClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 98%, ce qui correspond à la précision du modèle original.
2.22.3. Représentation ONNX du Classificateur Perceptron Multi-couche
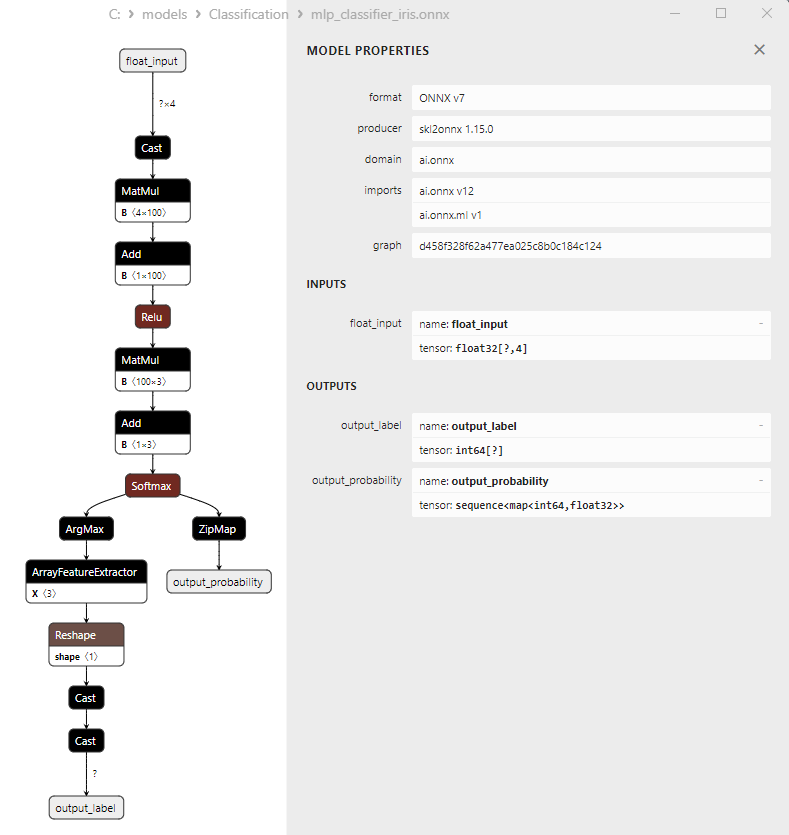
Figure 36. Représentation ONNX du Classificateur Perceptron Multicouche dans Netron
2.23. Classificateur Linear Discriminant Analysis (LDA)
Le Classificateur Linear Discriminant Analysis (LDA) est une méthode d'apprentissage automatique utilisée pour les tâches de classification. Elle appartient à la famille des méthodes de réduction de la dimensionnalité et de classification dans un espace de dimension inférieure. LDA construit des hyper-plans pour maximiser la séparation entre les classes.
Principes du Classificateur LDA :
- Réduction de la Dimensionnalité : L'idée centrale du LDA est la réduction de la dimensionnalité. Elle vise à trouver un nouvel espace de caractéristiques où les classes de données sont séparées au maximum.
- Maximiser la Séparation : LDA construit des hyper-plans (combinaisons linéaires de caractéristiques) qui maximisent la différence entre les valeurs moyennes des caractéristiques dans différentes classes et minimisent la variance au sein de chaque classe.
- Paramètres de Formation : Le modèle LDA est formé sur l'ensemble des données d'apprentissage, en calculant les paramètres des hyper-plans et des projections de données dans le nouvel espace de caractéristiques.
Avantages du Classificateur LDA :
- Amélioration de la Séparation des Classes : LDA peut améliorer de manière significative la séparation des classes dans les données, en particulier dans les cas où les classes se chevauchent fortement dans l'espace des caractéristiques d'origine.
- Réduction de la Dimensionnalité : LDA peut également être utilisé pour réduire la dimensionnalité des données, ce qui peut être utile pour la visualisation et la réduction de la complexité de calcul.
Limites du Classificateur LDA :
- Hypothèse de Normalité : LDA suppose que les caractéristiques suivent une distribution normale et que les classes ont des matrices de covariance égales. Si ces hypothèses ne sont pas respectées, la LDA peut fournir des résultats moins précis.
- Sensibilité aux Valeurs Aberrantes : LDA peut être sensible aux valeurs aberrantes des données car elles peuvent affecter les calculs des paramètres du modèle.
- Défis en matière de Classification Multi-classe : LDA a été développé à l'origine pour la classification binaire, et son extension à des tâches multi-classes nécessite une adaptation.
Le Classificateur LDA est une méthode précieuse pour les tâches de classification et de réduction de la dimensionnalité, en particulier lorsqu'il est nécessaire d'améliorer la séparation des classes. Il est fréquemment utilisé dans les statistiques, la biologie, l'analyse médicale et d'autres domaines pour l'analyse et la classification des données.
2.23.1. Code de Création du Modèle de Classification de l'Analyse Discriminante Linéaire (LDA)
Ce code démontre le processus d'entraînement d'un Classificateur d'Analyse Discriminante Linéaire (LDA) sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_LDAClassifier.py # The code demonstrates the process of training Linear Discriminant Analysis (LDA) Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Linear Discriminant Analysis (LDA) Classifier model lda_model = LinearDiscriminantAnalysis() # train the model on the entire dataset lda_model.fit(X, y) # predict classes for the entire dataset y_pred = lda_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Linear Discriminant Analysis (LDA) Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(lda_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"lda_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\lda_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Linear Discriminant Analysis (LDA) Classifier model in ONNX format: 0.98
2.23.2. Code MQL5 pour Travailler avec le Modèle de Classification de l'Analyse Discriminante Linéaire (LDA)
//+------------------------------------------------------------------+ //| Iris_LDAClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "lda_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="LDAClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_LDAClassifier (EURUSD,H1) model:LDAClassifier correct results: 98.00% Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier all samples accuracy=0.980000 Iris_LDAClassifier (EURUSD,H1) model=LDAClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 98%, ce qui correspond à la précision du modèle original.
2.23.3. Représentation ONNX du Classificateur Linear Discriminant Analysis (LDA)
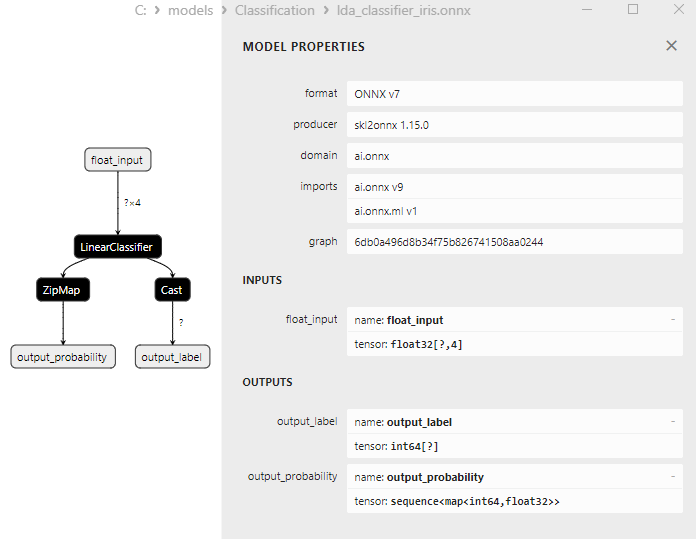
Figure 37. Représentation ONNX du Classificateur Linear Discriminant Analysis (LDA) dans Netron
2.24. Hist Gradient Boosting
Le classificateur Hist Gradient Boosting est un algorithme d'apprentissage automatique qui appartient à la famille du gradient boosting et qui est conçu pour les tâches de classification. Il s'agit d'une méthode efficace et puissante largement utilisée dans l'analyse des données et l'apprentissage automatique.
Principes du Classificateur Hist Gradient Boosting :
- Renforcement du Gradient : Le Classificateur Hist Gradient Boosting est basé sur la méthode du gradient boosting, qui construit un ensemble d'arbres de décision pour améliorer la classification. Pour cela, il entraîne séquentiellement des modèles faibles et corrige les erreurs des modèles précédents.
- Utilisation de l'Histogramme : Le terme "Hist" dans le nom indique que cet algorithme utilise des histogrammes pour un traitement efficace des données. Au lieu de procéder à une énumération exhaustive des caractéristiques, le Hist Gradient Boosting construit des histogrammes de caractéristiques, ce qui permet de construire rapidement un arbre de décision.
- Formation sur les Résidus : Comme les autres méthodes de renforcement du gradient, la méthode Hist Gradient Boosting entraîne chaque nouvel arbre sur les résidus du modèle précédent afin d'affiner les prédictions.
Avantages du Classificateur Hist Gradient Boosting :
- Haute Précision : Le classificateur Hist Gradient Boosting offre généralement une grande précision de classification, en particulier lorsqu'il utilise un grand nombre d'arbres.
- Efficacité : L'utilisation d'histogrammes permet à l'algorithme de traiter efficacement de grands ensembles de données et de construire rapidement un ensemble.
- Capacité à Traiter des Données Hétérogènes : L'algorithme peut traiter des données hétérogènes, y compris des caractéristiques catégorielles et numériques.
Limites du Classificateur Hist Gradient Boosting :
- Sensibilité au Sur-Ajustement : Lorsque les paramètres ne sont pas correctement réglés ou lorsqu'un grand nombre d'arbres sont utilisés, le Classificateur Hist Gradient Boosting peut être sujet à un sur-ajustement.
- Réglage des Paramètres : Comme les autres algorithmes de renforcement du gradient, le Hist Gradient Boosting nécessite un réglage minutieux des paramètres pour obtenir des performances optimales.
Le Classificateur Hist Gradient Boosting est un algorithme puissant pour les tâches de classification et de régression qui offre une grande précision et une grande efficacité dans le traitement des données. Il trouve des applications dans divers domaines, tels que l'analyse de données, la bio-informatique, la finance, etc.
2.24.1. Code pour la Création du Modèle de Classification Histogram-Based Gradient Boosting
Ce code démontre le processus d'entraînement d'un Classificateur Histogram-Based Gradient Boosting sur l'ensemble de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_HistGradientBoostingClassifier.py # The code demonstrates the process of training Histogram-Based Gradient Boosting Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a Histogram-Based Gradient Boosting Classifier model hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) # train the model on the entire dataset hist_gradient_boosting_model.fit(X, y) # predict classes for the entire dataset y_pred = hist_gradient_boosting_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of Hist Gradient Boosting Classifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path +"hist_gradient_boosting_classifier_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of Hist Gradient Boosting Classifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Hist Gradient Boosting Classifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\hist_gradient_boosting_classifier_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of Hist Gradient Boosting Classifier model in ONNX format: 1.0
2.24.2. Code MQL5 pour Travailler avec le Modèle de Classification Histogram-Based Gradient Boosting
//+------------------------------------------------------------------+ //| Iris_HistGradientBoostingClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "hist_gradient_boosting_classifier_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="HistGradientBoostingClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_HistGradientBoostingClassifier (EURUSD,H1) model:HistGradientBoostingClassifier correct results: 100.00% Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier all samples accuracy=1.000000 Iris_HistGradientBoostingClassifier (EURUSD,H1) model=HistGradientBoostingClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 100%, ce qui correspond à la précision du modèle original.
2.24.3. Représentation ONNX du Classificateur Histogram-Based Gradient Boosting
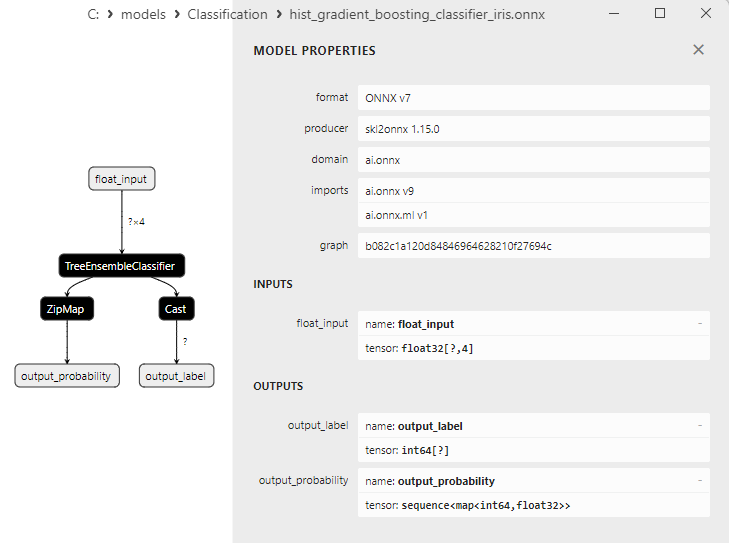
Figure 38. Représentation ONNX du Classificateur Histogram-Based Gradient Boosting dans Netron
2.25. Classificateur CategoricalNB
CategoricalNB est un algorithme de classification basé sur le théorème de Bayes. Il est spécialement conçu pour les ensembles de données comportant des caractéristiques catégorielles et est largement utilisé dans la classification des textes, la détection des spams et d'autres applications impliquant des données discrètes.
Principes de CategoricalNB :
- Classificateur Naive Bayes : CategoricalNB est un type de classificateur naïf de Bayes basé sur le théorème de Bayes. Il calcule la probabilité d'appartenir à une classe particulière pour un ensemble de caractéristiques en utilisant les probabilités conditionnelles de chaque caractéristique compte tenu de la classe.
- Caractéristiques Catégorielles : Contrairement au classificateur Gaussien Naive Bayes, qui suppose des caractéristiques continues avec une distribution normale, CategoricalNB est adapté aux ensembles de données comportant des caractéristiques catégorielles. Il modélise la distribution de probabilité de chaque caractéristique pour chaque classe.
- Hypothèse d’Indépendance : Le terme "naïf" dans le classificateur de Bayes naïf provient de l'hypothèse d'indépendance des caractéristiques. CategoricalNB suppose que les caractéristiques sont conditionnellement indépendantes compte tenu de la classe. Bien que cette hypothèse ne soit pas toujours respectée dans la pratique, les méthodes de Bayes naïves peuvent donner de bons résultats sur de nombreux ensembles de données du monde réel.
Avantages de CategoricalNB :
- Efficacité : CategoricalNB est efficace sur le plan des calculs et peut s'adapter à de grands ensembles de données. Il nécessite un minimum de mémoire et peut fournir des prédictions rapides.
- Interprétabilité : Sa nature probabiliste rend CategoricalNB interprétable. Il peut fournir des indications sur les caractéristiques qui influencent la prédiction.
- Traitement des Données Catégorielles : CategoricalNB est spécialement conçu pour les ensembles de données comportant des caractéristiques catégorielles. Il peut traiter efficacement des données textuelles et d'autres types de caractéristiques discrètes.
- Performance de Référence : Il sert souvent de modèle de base solide pour les tâches de classification de textes et peut surpasser des algorithmes plus complexes sur de petits ensembles de données.
Limites de CategoricalNB :
- Hypothèse d’Indépendance : L'hypothèse de l'indépendance des caractéristiques peut ne pas être valable pour tous les ensembles de données. Si les caractéristiques sont très dépendantes, les performances de CategoricalNB peuvent se détériorer.
- Sensibilité à la Mise à l'Echelle des Caractéristiques : CategoricalNB ne nécessite pas de mise à l'échelle des caractéristiques puisqu'il travaille avec des données catégorielles. Mais dans certains cas, la normalisation ou l'encodage des caractéristiques catégorielles de différentes manières peut affecter ses performances.
- Expression Limitée : CategoricalNB peut ne pas capturer des dépendances de données complexes ainsi que des algorithmes plus complexes, tels que les modèles d'apprentissage profond.
- Traitement des Données Manquantes : Il suppose qu'il n'y a pas de valeurs manquantes dans l'ensemble de données et que les valeurs manquantes doivent être prétraitées.
CategoricalNB est un algorithme de classification précieux, particulièrement adapté aux ensembles de données comportant des caractéristiques catégorielles. Sa simplicité, son efficacité et sa facilité d'interprétation en font un outil utile pour diverses tâches de classification. Malgré des limitations telles que l'hypothèse d'indépendance, il reste un choix populaire pour la classification des textes et d'autres tâches où les données discrètes dominent. Lorsque l'on travaille avec des données catégorielles, considérer CategoricalNB comme un modèle de base est souvent un choix raisonnable. Mais il est important d'évaluer ses performances par rapport à des modèles plus complexes, en particulier s'il existe des dépendances dans les données.
2.25.1. Code pour la Création du Modèle de Classification CategoricalNB
Ce code démontre le processus d'entraînement d'un Classificateur CategoricalNB sur le jeu de données Iris, l'exportant au format ONNX, et effectuant la classification en utilisant le modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_CategoricalNBClassifier.py # The code demonstrates the process of training CategoricalNB Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.naive_bayes import CategoricalNB from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create a CategoricalNB model categorical_nb_model = CategoricalNB() # train the model on the entire dataset categorical_nb_model.fit(X, y) # predict classes for the entire dataset y_pred = categorical_nb_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of CategoricalNB model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(categorical_nb_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "categorical_nb_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of CategoricalNB model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of CategoricalNB model: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.86 0.96 0.91 50
Python 2 0.95 0.84 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.94 0.93 0.93 150
Python weighted avg 0.94 0.93 0.93 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\categorical_nb_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of CategoricalNB model in ONNX format: 0.9333333333333333
2.25.2. Code MQL5 pour Travailler avec le Modèle de Classification CategoricalNB
//+------------------------------------------------------------------+ //| Iris_CategoricalNBClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "categorical_nb_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="CategoricalNBClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+Sortie :
Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier correct results: 93.33% Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier all samples accuracy=0.933333 Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80) Iris_CategoricalNBClassifier (EURUSD,H1) model:CategoricalNBClassifier FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90) Iris_CategoricalNBClassifier (EURUSD,H1) model=CategoricalNBClassifier batch test accuracy=0.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 93,33%, ce qui correspond à la précision du modèle original.
2.25.3. Représentation ONNX du Classificateur CategoricalNB
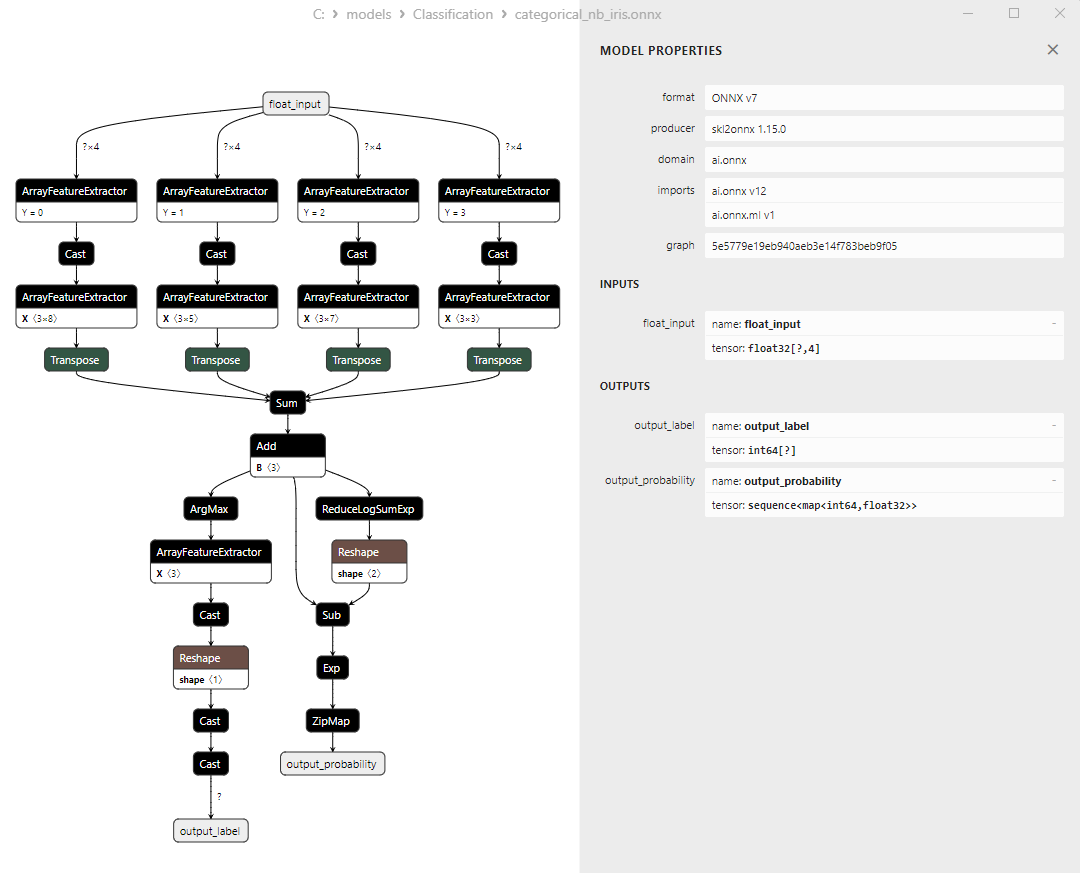
Figure 39. Représentation ONNX du Classificateur CategoricalNB dans Netron
Note sur les modèles ExtraTreeClassifier et ExtraTreesClassifier
ExtraTreeClassifier et ExtraTreesClassifier sont deux classificateurs différents. La principale différence réside dans leur mode de fonctionnement :
ExtraTreeClassifier (Classificateur d'Arbres Extrêmement Aléatoires) :
- Ce classificateur est également connu sous le nom de Extremely Randomized Trees ou Extra-Trees.
- Il est basé sur l'idée d'arbres de décision aléatoires.
- Dans ExtraTreeClassifier, le choix de la division pour chaque nœud de l'arbre se fait de manière aléatoire, sans recherche préalable de la meilleure division.
- Le classificateur est donc moins gourmand en ressources de calcul que la forêt aléatoire classique, car il ne nécessite pas le calcul des divisions optimales pour chaque nœud.
- ExtraTreeClassifier utilise souvent des seuils aléatoires pour les caractéristiques et un découpage aléatoire, ce qui se traduit par des arbres plus aléatoires.
- L'absence de recherche des meilleures divisions rend ExtraTreeClassifier plus rapide mais moins précis que Random Forest.
ExtraTreesClassifier (Classificateur d'Arbres Extrêmement Aléatoires) :
- ExtraTreesClassifier est également un classificateur basé sur la méthode des arbres extrêmement aléatoires.
- La principale différence entre ExtraTreesClassifier et ExtraTreeClassifier est que ExtraTreesClassifier effectue des scissions aléatoires pour choisir les meilleures scissions à chaque nœud de l'arbre.
- Cela signifie que ExtraTreesClassifier applique une forêt aléatoire avec un niveau d'aléa supplémentaire lors de la sélection des divisions optimales.
- ExtraTreesClassifier est généralement plus précis que ExtraTreeClassifier car il effectue des divisions aléatoires pour trouver les meilleures caractéristiques à diviser.
- Mais ExtraTreesClassifier peut être plus exigeant en termes de calcul en raison de la nécessité d'effectuer une recherche plus large des divisions optimales.
En résumé : la principale différence entre ces deux classificateurs réside dans le niveau d'aléa dans la sélection des fractions. ExtraTreeClassifier effectue un choix aléatoire pour chaque nœud sans rechercher les meilleures répartitions, alors que ExtraTreesClassifier effectue des répartitions aléatoires tout en recherchant les répartitions optimales à chaque nœud.
2.26. ExtraTreeClassifier
Principes de ExtraTreeClassifier :
- Séparation Aléatoire des Nœuds : Le principe de base de ExtraTreeClassifier est qu'il sélectionne aléatoirement la division pour chaque nœud de l'arbre. Cette méthode diffère des arbres de décision traditionnels, qui choisissent la meilleure caractéristique pour la division. ExtraTreeClassifier effectue des scissions sans tenir compte de la meilleure scission, ce qui le rend plus aléatoire et plus résistant à l'ajustement excessif.
- Agrégation des Résultats : Lors de la construction de l'ensemble, ExtraTreeClassifier crée plusieurs arbres aléatoires et regroupe leurs résultats. Cela permet d'améliorer la généralisation du modèle et de réduire la variance. Un ensemble d'arbres permet de lutter contre l'ajustement excessif et d'accroître la stabilité des prédictions.
- Seuils Aléatoires : Lors de la division des nœuds, ExtraTreeClassifier sélectionne des seuils aléatoires pour chaque caractéristique plutôt que des valeurs optimales spécifiques. Cela introduit plus d'aléa et de stabilité du modèle.
- Résistance au Sur-Ajustement : Grâce aux divisions aléatoires et à l'absence de sélection de la meilleure division, ExtraTreeClassifier est généralement moins enclin à la sur-adaptation que les arbres de décision classiques.
- Vitesse d'Entraînement Elevée : ExtraTreeClassifier nécessite moins de ressources de calcul pour l'apprentissage que de nombreux autres algorithmes, tels que les forêts aléatoires. Il est donc rapide et efficace pour les grands ensembles de données.
- Polyvalence : ExtraTreeClassifier peut être utilisé pour des tâches de classification et de régression, ce qui en fait un algorithme polyvalent pour différents types de problèmes.
- Aléatoire : L'utilisation de divisions aléatoires peut conduire à des modèles moins précis dans certains cas. Il est important de régler les paramètres avec soin.
- Sensibilité aux Valeurs Aberrantes : ExtraTreeClassifier peut être sensible aux valeurs aberrantes des données, car il crée des divisions aléatoires. Cela peut entraîner des prédictions instables dans certains cas.
- Interprétabilité Réduite : Par rapport aux arbres de décision classiques, ExtraTreeClassifier est moins facile à interpréter et à expliquer.
2.26.1. Code de Création du Modèle ExtraTreeClassifier
Ce code démontre le processus d'entraînement d'un modèle de Classificateur ExtraTreeClassifier sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_ExtraTreeClassifier.py # The code demonstrates the process of training ExtraTree Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.tree import ExtraTreeClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreeClassifier model extra_tree_model = ExtraTreeClassifier() # train the model on the entire dataset extra_tree_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_tree_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreeClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_tree_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_tree_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreeClassifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of ExtraTreeClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_tree_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreeClassifier model in ONNX format: 1.0
2.26.2. Code MQL5 pour Travailler avec le Modèle ExtraTreeClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreeClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_tree_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreeClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_ExtraTreeClassifier (EURUSD,H1) model:ExtraTreeClassifier correct results: 100.00% Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier all samples accuracy=1.000000 Iris_ExtraTreeClassifier (EURUSD,H1) model=ExtraTreeClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 100%, ce qui correspond à la précision du modèle original.
2.26.3. Représentation ONNX du Classificateur ExtraTreeClassifier
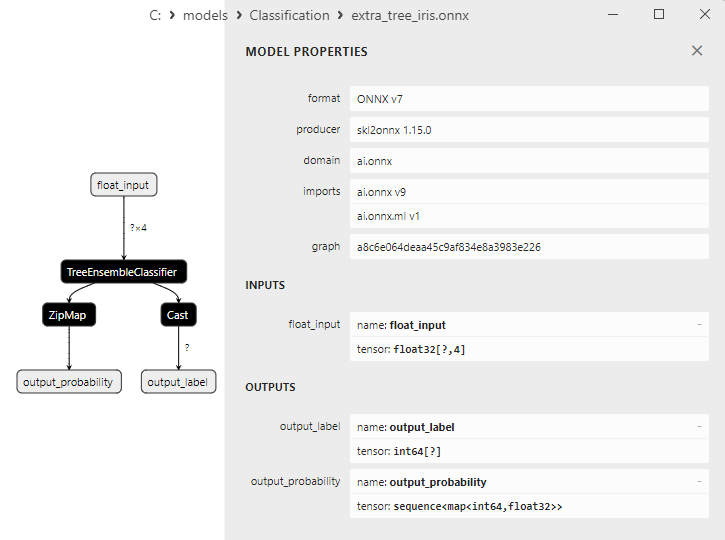
Figure 40. Représentation ONNX de ExtraTreeClassifier dans Netron
2.27. ExtraTreesClassifier
ExtraTreesClassifier est un puissant algorithme d'apprentissage automatique utilisé pour les tâches de classification. Cet algorithme est une extension et une amélioration de Random Forest, offrant plusieurs avantages et inconvénients.Principes de ExtraTreesClassifier :
- Échantillonnage Bootstrap : Comme Random Forest, ExtraTreesClassifier utilise la méthode bootstrap pour créer plusieurs sous-échantillons à partir de l'ensemble de données d'apprentissage. Cela signifie que pour chaque arbre, un sous-échantillon aléatoire avec remplacement est créé à partir des données d’origine.
- Divisions Aléatoires : Contrairement à Random Forest, où la meilleure caractéristique pour la division est choisie pour chaque nœud de l'arbre, ExtraTreesClassifier utilise des caractéristiques et des seuils aléatoires pour diviser les nœuds. Cela rend les arbres plus aléatoires et réduit le sur-ajustement.
- Vote : Après avoir construit un ensemble d'arbres, chaque arbre vote pour la classe de l'objet. Finalement, la classe ayant obtenu le plus grand nombre de votes devient la classe prédite.
- Réduction du Sur-Ajustement : L'utilisation de divisions et de caractéristiques aléatoires rend le classificateur ExtraTreesClassifier moins enclin au sur-ajustement que les arbres de décision traditionnels.
- Vitesse d'Entraînement Elevée : Le classificateur ExtraTreesClassifier nécessite moins de ressources de calcul pour l'apprentissage que d'autres algorithmes, tels que le gradient boosting. Il est donc rapide et efficace, en particulier pour les grands ensembles de données.
- Robustesse aux Valeurs Aberrantes : Grâce à l'ensemble d'arbres et aux divisions aléatoires, le classificateur ExtraTreesClassifier est généralement plus robuste face aux données aberrantes.
- Interprétabilité Complexe : L'analyse et l'interprétation d'un modèle ExtraTreesClassifier peuvent s'avérer difficiles en raison du grand nombre de divisions et de caractéristiques aléatoires.
- Réglage des Paramètres : Malgré son efficacité, ExtraTreesClassifier peut nécessiter un réglage minutieux des hyper-paramètres pour obtenir des performances optimales.
- Pas Toujours Le Plus Performant : Dans certaines tâches, ExtraTreesClassifier peut être moins précis que d'autres algorithmes, tels que le gradient boosting.
2.27.1. Code de Création du Modèle ExtraTreesClassifier
Ce code démontre le processus d'entraînement d'un modèle ExtraTreesClassifier sur le jeu de données Iris, son export au format ONNX et la réalisation d'une classification à l'aide du modèle ONNX. Il évalue également la précision du modèle original et du modèle ONNX.
# Iris_ExtraTreesClassifier.py # The code demonstrates the process of training ExtraTrees Classifier model on the Iris dataset, exporting it to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original model and the ONNX model. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.ensemble import ExtraTreesClassifier from sklearn.metrics import accuracy_score, classification_report from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create an ExtraTreesClassifier model extra_trees_model = ExtraTreesClassifier() # train the model on the entire dataset extra_trees_model.fit(X, y) # predict classes for the entire dataset y_pred = extra_trees_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) print("Accuracy of ExtraTreesClassifier model:", accuracy) # display the classification report print("\nClassification Report:\n", classification_report(y, y_pred)) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(extra_trees_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + "extra_trees_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # print model path print(f"Model saved to {onnx_filename}") # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # display information about input tensors in ONNX print("\nInformation about input tensors in ONNX:") for i, input_tensor in enumerate(onnx_session.get_inputs()): print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}") # display information about output tensors in ONNX print("\nInformation about output tensors in ONNX:") for i, output_tensor in enumerate(onnx_session.get_outputs()): print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}") # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) print("\nAccuracy of ExtraTreesClassifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of ExtraTreesClassifier model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\extra_trees_iris.onnx
Python
Python Information about input tensors in ONNX:
Python 1. Name: float_input, Data Type: tensor(float), Shape: [None, 4]
Python
Python Information about output tensors in ONNX:
Python 1. Nom : output_label, Type de Données : tensor(int64), Forme : [None]
Python 2. Name: output_probability, Data Type: seq(map(int64,tensor(float))), Shape: []
Python
Python Accuracy of ExtraTreesClassifier model in ONNX format: 1.
2.27.2. Code MQL5 pour Travailler avec le Modèle ExtraTreesClassifier
//+------------------------------------------------------------------+ //| Iris_ExtraTreesClassifier.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" #resource "extra_trees_iris.onnx" as const uchar ExtModel[]; //+------------------------------------------------------------------+ //| Test IRIS dataset samples | //+------------------------------------------------------------------+ bool TestSamples(long model,float &input_data[][4], int &model_classes_id[]) { //--- check number of input samples ulong batch_size=input_data.Range(0); if(batch_size==0) return(false); //--- prepare output array ArrayResize(model_classes_id,(int)batch_size); //--- float output_data[]; //--- struct Map { ulong key[]; float value[]; } output_data_map[]; //--- check consistency bool res=ArrayResize(output_data,(int)batch_size)==batch_size; //--- if(res) { //--- set input shape ulong input_shape[]= {batch_size,input_data.Range(1)}; OnnxSetInputShape(model,0,input_shape); //--- set output shapeы ulong output_shape1[]= {batch_size}; ulong output_shape2[]= {batch_size}; OnnxSetOutputShape(model,0,output_shape1); OnnxSetOutputShape(model,1,output_shape2); //--- run the model res=OnnxRun(model,0,input_data,output_data,output_data_map); //--- postprocessing if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- for(uint n=0; n<output_data_map.Size(); n++) { int model_class_id=-1; int max_idx=-1; float max_value=-1; //--- copy to arrays ArrayCopy(output_keys,output_data_map[n].key); ArrayCopy(output_values,output_data_map[n].value); //ArrayPrint(output_keys); //ArrayPrint(output_values); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } //--- store the result to the output array model_classes_id[n]=model_class_id; //Print("model_class_id=",model_class_id); } } } //--- return(res); } //+------------------------------------------------------------------+ //| Test all samples from IRIS dataset (150) | //| Here we test all samples with batch=1, sample by sample | //+------------------------------------------------------------------+ bool TestAllIrisDataset(const long model,const string model_name,double &model_accuracy) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("iris dataset not prepared"); return(false); } //--- show dataset for(int k=0; k<total_samples; k++) { //PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); } //--- array for output classes int model_output_classes_id[]; //--- check all Iris dataset samples int correct_results=0; for(int k=0; k<total_samples; k++) { //--- input array float iris_sample_input_data[1][4]; //--- prepare input data from kth iris sample dataset iris_sample_input_data[0][0]=(float)iris_samples[k].features[0]; iris_sample_input_data[0][1]=(float)iris_samples[k].features[1]; iris_sample_input_data[0][2]=(float)iris_samples[k].features[2]; iris_sample_input_data[0][3]=(float)iris_samples[k].features[3]; //--- run model bool res=TestSamples(model,iris_sample_input_data,model_output_classes_id); //--- check result if(res) { if(model_output_classes_id[0]==iris_samples[k].class_id) { correct_results++; } else { PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_output_classes_id[0],iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } } model_accuracy=1.0*correct_results/total_samples; //--- PrintFormat("model:%s correct results: %.2f%%",model_name,100*model_accuracy); //--- return(true); } //+------------------------------------------------------------------+ //| Here we test batch execution of the model | //+------------------------------------------------------------------+ bool TestBatchExecution(const long model,const string model_name,double &model_accuracy) { model_accuracy=0; //--- array for output classes int model_output_classes_id[]; int correct_results=0; int total_results=0; bool res=false; //--- run batch with 3 samples float input_data_batch3[3][4]= { {5.1f,3.5f,1.4f,0.2f}, // iris dataset sample id=1, Iris-setosa {6.3f,2.5f,4.9f,1.5f}, // iris dataset sample id=73, Iris-versicolor {6.3f,2.7f,4.9f,1.8f} // iris dataset sample id=124, Iris-virginica }; int correct_classes_batch3[3]= {0,1,2}; //--- run model res=TestSamples(model,input_data_batch3,model_output_classes_id); if(res) { //--- check result for(int j=0; j<ArraySize(model_output_classes_id); j++) { //--- check result if(model_output_classes_id[j]==correct_classes_batch3[j]) correct_results++; else { PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch3[j],input_data_batch3[j][0],input_data_batch3[j][1],input_data_batch3[j][2],input_data_batch3[j][3]); } total_results++; } } else return(false); //--- run batch with 10 samples float input_data_batch10[10][4]= { {5.5f,3.5f,1.3f,0.2f}, // iris dataset sample id=37 (Iris-setosa) {4.9f,3.1f,1.5f,0.1f}, // iris dataset sample id=38 (Iris-setosa) {4.4f,3.0f,1.3f,0.2f}, // iris dataset sample id=39 (Iris-setosa) {5.0f,3.3f,1.4f,0.2f}, // iris dataset sample id=50 (Iris-setosa) {7.0f,3.2f,4.7f,1.4f}, // iris dataset sample id=51 (Iris-versicolor) {6.4f,3.2f,4.5f,1.5f}, // iris dataset sample id=52 (Iris-versicolor) {6.3f,3.3f,6.0f,2.5f}, // iris dataset sample id=101 (Iris-virginica) {5.8f,2.7f,5.1f,1.9f}, // iris dataset sample id=102 (Iris-virginica) {7.1f,3.0f,5.9f,2.1f}, // iris dataset sample id=103 (Iris-virginica) {6.3f,2.9f,5.6f,1.8f} // iris dataset sample id=104 (Iris-virginica) }; //--- correct classes for all 10 samples in the batch int correct_classes_batch10[10]= {0,0,0,0,1,1,2,2,2,2}; //--- run model res=TestSamples(model,input_data_batch10,model_output_classes_id); //--- check result if(res) { for(int j=0; j<ArraySize(model_output_classes_id); j++) { if(model_output_classes_id[j]==correct_classes_batch10[j]) correct_results++; else { double f1=input_data_batch10[j][0]; double f2=input_data_batch10[j][1]; double f3=input_data_batch10[j][2]; double f4=input_data_batch10[j][3]; PrintFormat("model:%s FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f)",model_name,model_output_classes_id[j],correct_classes_batch10[j],input_data_batch10[j][0],input_data_batch10[j][1],input_data_batch10[j][2],input_data_batch10[j][3]); } total_results++; } } else return(false); //--- calculate accuracy model_accuracy=correct_results/total_results; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { string model_name="ExtraTreesClassifier"; //--- long model=OnnxCreateFromBuffer(ExtModel,ONNX_DEFAULT); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- test all dataset double model_accuracy=0; //-- test sample by sample execution for all Iris dataset if(TestAllIrisDataset(model,model_name,model_accuracy)) PrintFormat("model=%s all samples accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- test batch execution for several samples if(TestBatchExecution(model,model_name,model_accuracy)) PrintFormat("model=%s batch test accuracy=%f",model_name,model_accuracy); else PrintFormat("error in testing model=%s ",model_name); //--- release model OnnxRelease(model); } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_ExtraTreesClassifier (EURUSD,H1) model:ExtraTreesClassifier correct results: 100.00% Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier all samples accuracy=1.000000 Iris_ExtraTreesClassifier (EURUSD,H1) model=ExtraTreesClassifier batch test accuracy=1.000000
La précision du modèle ONNX exporté sur l'ensemble du jeu de données Iris est de 100%, ce qui correspond à la précision du modèle original.
2.27.3. Représentation ONNX de ExtraTreesClassifier
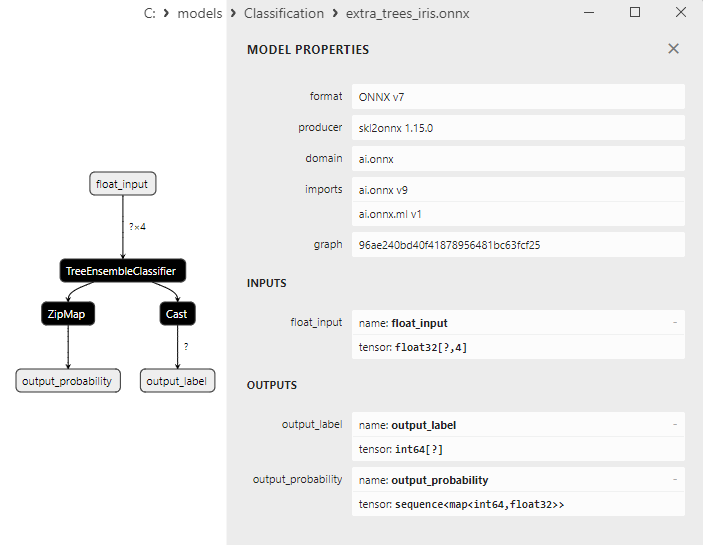
Figure 41. Représentation ONNX de ExtraTreesClassifier dans Netron
2.28. Comparaison de la Précision de Tous les Modèles
Considérons maintenant tous les modèles ensemble et comparons leurs performances. Nous effectuerons tout d’abord la comparaison en utilisant Python, puis nous chargerons et exécuterons les modèles ONNX sauvegardés dans MetaTrader 5.
2.28.1. Code pour le Calcul de Tous les Modèles et Elaboration d'un Tableau de Comparaison de la Précision
Ce script calcule 27 modèles de classification à partir du paquet Scikit-learn sur l'ensemble des données Iris de Fisher, exporte les modèles au format ONNX, les exécute et compare la précision des modèles originaux et des modèles ONNX.
# Iris_AllClassifiers.py # The code demonstrates the process of training 27 Classifier models on the Iris dataset, exports them to ONNX format, and making predictions using the ONNX model. # It also evaluates the accuracy of both the original and the ONNX models. # Copyright 2023, MetaQuotes Ltd. # https://www.mql5.com # import necessary libraries from sklearn import datasets from sklearn.metrics import accuracy_score from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType import onnxruntime as ort import numpy as np import matplotlib.pyplot as plt from sys import argv # define the path for saving the model data_path = argv[0] last_index = data_path.rfind("\\") + 1 data_path = data_path[0:last_index] # load the Iris dataset iris = datasets.load_iris() X = iris.data y = iris.target # create and train each classifier model from sklearn.svm import SVC svc_model = SVC() svc_model.fit(X, y) from sklearn.ensemble import RandomForestClassifier random_forest_model = RandomForestClassifier(random_state=42) random_forest_model.fit(X, y) from sklearn.ensemble import GradientBoostingClassifier gradient_boosting_model = GradientBoostingClassifier(random_state=42) gradient_boosting_model.fit(X, y) from sklearn.ensemble import AdaBoostClassifier adaboost_model = AdaBoostClassifier(random_state=42) adaboost_model.fit(X, y) from sklearn.ensemble import BaggingClassifier bagging_model = BaggingClassifier(random_state=42) bagging_model.fit(X, y) from sklearn.neighbors import KNeighborsClassifier knn_model = KNeighborsClassifier() knn_model.fit(X, y) from sklearn.neighbors import RadiusNeighborsClassifier radius_neighbors_model = RadiusNeighborsClassifier(radius=1.0) radius_neighbors_model.fit(X, y) from sklearn.tree import DecisionTreeClassifier decision_tree_model = DecisionTreeClassifier(random_state=42) decision_tree_model.fit(X, y) from sklearn.linear_model import LogisticRegression logistic_regression_model = LogisticRegression(max_iter=1000, random_state=42) logistic_regression_model.fit(X, y) from sklearn.linear_model import RidgeClassifier ridge_classifier_model = RidgeClassifier(random_state=42) ridge_classifier_model.fit(X, y) from sklearn.linear_model import PassiveAggressiveClassifier passive_aggressive_model = PassiveAggressiveClassifier(max_iter=1000, random_state=42) passive_aggressive_model.fit(X, y) from sklearn.linear_model import Perceptron perceptron_model = Perceptron(max_iter=1000, random_state=42) perceptron_model.fit(X, y) from sklearn.linear_model import SGDClassifier sgd_model = SGDClassifier(max_iter=1000, random_state=42) sgd_model.fit(X, y) from sklearn.naive_bayes import GaussianNB gaussian_nb_model = GaussianNB() gaussian_nb_model.fit(X, y) from sklearn.naive_bayes import MultinomialNB multinomial_nb_model = MultinomialNB() multinomial_nb_model.fit(X, y) from sklearn.naive_bayes import ComplementNB complement_nb_model = ComplementNB() complement_nb_model.fit(X, y) from sklearn.naive_bayes import BernoulliNB bernoulli_nb_model = BernoulliNB() bernoulli_nb_model.fit(X, y) from sklearn.naive_bayes import CategoricalNB categorical_nb_model = CategoricalNB() categorical_nb_model.fit(X, y) from sklearn.tree import ExtraTreeClassifier extra_tree_model = ExtraTreeClassifier(random_state=42) extra_tree_model.fit(X, y) from sklearn.ensemble import ExtraTreesClassifier extra_trees_model = ExtraTreesClassifier(random_state=42) extra_trees_model.fit(X, y) from sklearn.svm import LinearSVC # Import LinearSVC linear_svc_model = LinearSVC(random_state=42) linear_svc_model.fit(X, y) from sklearn.svm import NuSVC nu_svc_model = NuSVC() nu_svc_model.fit(X, y) from sklearn.linear_model import LogisticRegressionCV logistic_regression_cv_model = LogisticRegressionCV(cv=5, max_iter=1000, random_state=42) logistic_regression_cv_model.fit(X, y) from sklearn.neural_network import MLPClassifier mlp_model = MLPClassifier(max_iter=1000, random_state=42) mlp_model.fit(X, y) from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda_model = LinearDiscriminantAnalysis() lda_model.fit(X, y) from sklearn.experimental import enable_hist_gradient_boosting from sklearn.ensemble import HistGradientBoostingClassifier hist_gradient_boosting_model = HistGradientBoostingClassifier(random_state=42) hist_gradient_boosting_model.fit(X, y) from sklearn.linear_model import RidgeClassifierCV ridge_classifier_cv_model = RidgeClassifierCV() ridge_classifier_cv_model.fit(X, y) # define a dictionary to store results results = {} # loop through the models for model_name, classifier_model in [ ('SVC Classifier', svc_model), ('Random Forest Classifier', random_forest_model), ('Gradient Boosting Classifier', gradient_boosting_model), ('AdaBoost Classifier', adaboost_model), ('Bagging Classifier', bagging_model), ('K-NN Classifier', knn_model), ('Radius Neighbors Classifier', radius_neighbors_model), ('Decision Tree Classifier', decision_tree_model), ('Logistic Regression Classifier', logistic_regression_model), ('Ridge Classifier', ridge_classifier_model), ('Ridge ClassifierCV', ridge_classifier_cv_model), ('Passive-Aggressive Classifier', passive_aggressive_model), ('Perceptron Classifier', perceptron_model), ('SGD Classifier', sgd_model), ('Gaussian Naive Bayes Classifier', gaussian_nb_model), ('Multinomial Naive Bayes Classifier', multinomial_nb_model), ('Complement Naive Bayes Classifier', complement_nb_model), ('Bernoulli Naive Bayes Classifier', bernoulli_nb_model), ('Categorical Naive Bayes Classifier', categorical_nb_model), ('Extra Tree Classifier', extra_tree_model), ('Extra Trees Classifier', extra_trees_model), ('LinearSVC Classifier', linear_svc_model), ('NuSVC Classifier', nu_svc_model), ('Logistic RegressionCV Classifier', logistic_regression_cv_model), ('MLP Classifier', mlp_model), ('Linear Discriminant Analysis Classifier', lda_model), ('Hist Gradient Boosting Classifier', hist_gradient_boosting_model) ]: # predict classes for the entire dataset y_pred = classifier_model.predict(X) # evaluate the model's accuracy accuracy = accuracy_score(y, y_pred) # define the input data type initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))] # export the model to ONNX format with float data type onnx_model = convert_sklearn(classifier_model, initial_types=initial_type, target_opset=12) # save the model to a file onnx_filename = data_path + f"{model_name.lower().replace(' ', '_')}_iris.onnx" with open(onnx_filename, "wb") as f: f.write(onnx_model.SerializeToString()) # load the ONNX model and make predictions onnx_session = ort.InferenceSession(onnx_filename) input_name = onnx_session.get_inputs()[0].name output_name = onnx_session.get_outputs()[0].name # convert data to floating-point format (float32) X_float32 = X.astype(np.float32) # predict classes for the entire dataset using ONNX y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0] # evaluate the accuracy of the ONNX model accuracy_onnx = accuracy_score(y, y_pred_onnx) # store results results[model_name] = { 'accuracy': accuracy, 'accuracy_onnx': accuracy_onnx } # print the accuracy of the original model and the ONNX model #print(f"{model_name} - Original Accuracy: {accuracy}, ONNX Accuracy: {accuracy_onnx}") # sort the models based on accuracy sorted_results = dict(sorted(results.items(), key=lambda item: item[1]['accuracy'], reverse=True)) # print the sorted results print("Sorted Results:") for model_name, metrics in sorted_results.items(): print(f"{model_name} - Original Accuracy: {metrics['accuracy']:.4f}, ONNX Accuracy: {metrics['accuracy_onnx']:.4f}") # create comparison plots for sorted results fig, ax = plt.subplots(figsize=(12, 8)) model_names = list(sorted_results.keys()) accuracies = [sorted_results[model_name]['accuracy'] for model_name in model_names] accuracies_onnx = [sorted_results[model_name]['accuracy_onnx'] for model_name in model_names] bar_width = 0.35 index = range(len(model_names)) bar1 = plt.bar(index, accuracies, bar_width, label='Model Accuracy') bar2 = plt.bar([i + bar_width for i in index], accuracies_onnx, bar_width, label='ONNX Accuracy') plt.xlabel('Models') plt.ylabel('Accuracy') plt.title('Comparison of Model and ONNX Accuracy (Sorted)') plt.xticks([i + bar_width / 2 for i in index], model_names, rotation=90, ha='center') plt.legend() plt.tight_layout() plt.show()
Sortie :
Python Sorted Results: Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333Le script génère également une image avec un résumé des résultats pour l'ensemble des 27 modèles.
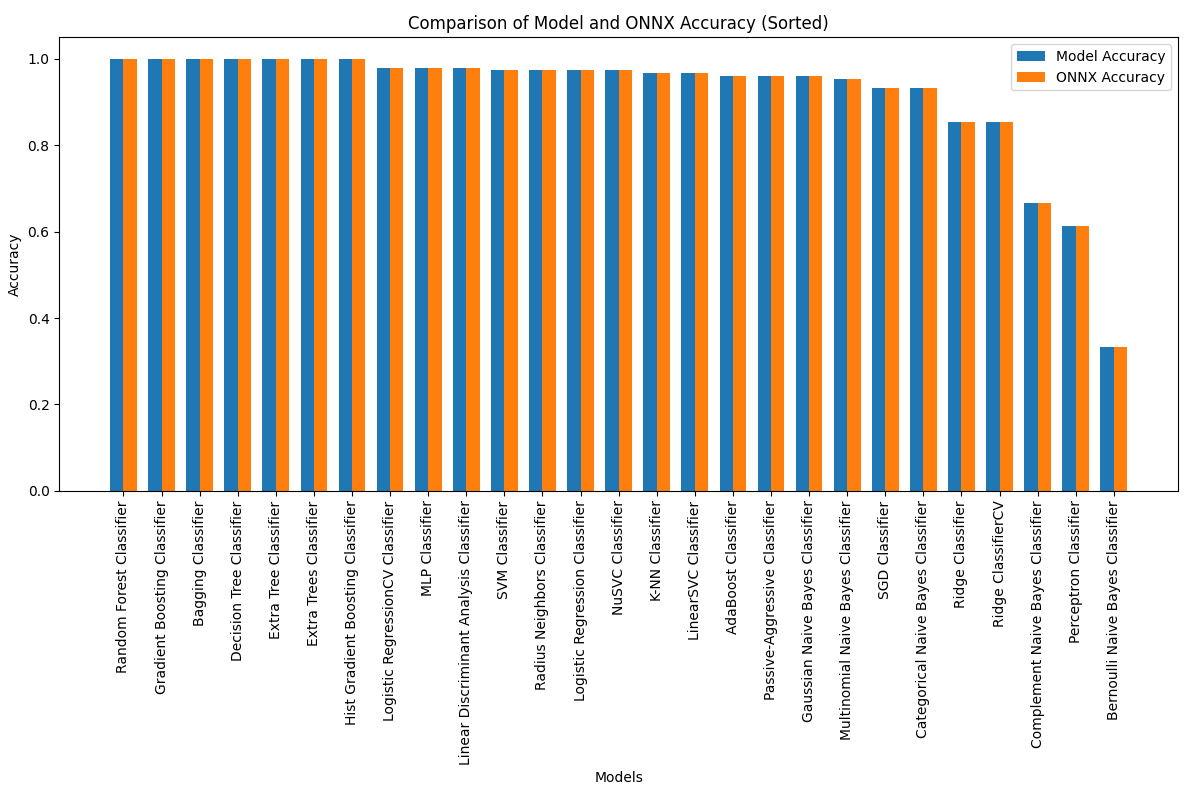
Figure 42. Comparaison de la Précision des 27 Modèles de Classification et de Leurs Versions ONNX sur le Jeu de Données Iris
Sur la base des résultats de l'évaluation de la précision des modèles originaux et de leurs versions ONNX, les conclusions suivantes peuvent être tirées :
Sept modèles ont montré une précision parfaite (1,0000) à la fois dans la version originale et dans la version ONNX. Ces modèles comprennent :
- Classificateur Random Forest
- Classificateur Gradient Boosting
- Classificateur Bagging
- Classificateur Decision Tree
- Classificateur Extra Tree
- Classificateur Extra Trees
- Classificateur Hist Gradient Boosting
Les représentations ONNX de ces modèles conservent également une grande précision.
Trois modèles - le Classificateur Logistic RegressionCV, le Classificateur MLP et le Classificateur Linear Discriminant Analysis - ont atteint une précision élevée dans les versions originales et ONNX, avec une précision de 0,9800. Ces modèles donnent de bons résultats dans les deux cas.
Plusieurs modèles, dont le Classificateur SVC, le Classificateur Radius Neighbors, le Classificateur NuSVC, le Classificateur K-NN, le Classificateur LinearSVC, le Classificateur AdaBoost, le Classificateur Passif-Agressif, le Classificateur Gaussian Naive Bayes et le Classificateur Multinomial Naive Bayes, ont montré une bonne précision à la fois dans la version originale et dans la version ONNX, avec des scores de précision de 0,9733, 0,9667 ou 0,9600. Ces modèles conservent également leur précision dans la représentation ONNX.
Les modèles tels que le Classificateur SGD, le Classificateur Categorical Naive Bayes, le Classificateur Ridge, le Classificateur Complement Naive Bayes, le Classificateur Perceptron, et le Classificateur Bernoulli Naive Bayes ont une précision plus faible, mais permettent de maintenir la précision dans ONNX.
Tous les modèles considérés conservent leur précision lorsqu'ils sont exportés au format ONNX, ce qui indique que ONNX constitue un moyen efficace de sauvegarder et de restaurer les modèles d'apprentissage automatique. Mais il est important de se rappeler que la qualité du modèle exporté peut dépendre de l'algorithme et des paramètres spécifiques du modèle.
2.28.2. Code MQL5 pour l'Exécution de Tous les Modèles ONNX
Ce script exécute tous les modèles ONNX sauvegardés par le script en 2.28.1 sur l'ensemble des données Iris de Fisher.
//+------------------------------------------------------------------+ //| Iris_AllClassifiers.mq5 | //| Copyright 2023, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2023, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include "iris.mqh" //+------------------------------------------------------------------+ //| TestSampleSequenceMapOutput | //+------------------------------------------------------------------+ bool TestSampleSequenceMapOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- float out1[]; //--- struct Map { ulong key[]; float value[]; } out2[]; //--- bool res=ArrayResize(out1,input_data.Range(0))==input_data.Range(0); //--- if(res) { ulong input_shape[]= { input_data.Range(0), input_data.Range(1) }; ulong output_shape[]= { input_data.Range(0) }; //--- OnnxSetInputShape(model,0,input_shape); OnnxSetOutputShape(model,0,output_shape); //--- res=OnnxRun(model,0,input_data,out1,out2); //--- if(res) { //--- postprocessing of sequence map data //--- find class with maximum probability ulong output_keys[]; float output_values[]; //--- model_class_id=-1; int max_idx=-1; float max_value=-1; //--- for(uint n=0; n<out2.Size(); n++) { //--- copy to arrays ArrayCopy(output_keys,out2[n].key); ArrayCopy(output_values,out2[n].value); //--- find the key with maximum probability for(int k=0; k<ArraySize(output_values); k++) { if(k==0) { max_idx=0; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } else { if(output_values[k]>max_value) { max_idx=k; max_value=output_values[max_idx]; model_class_id=(int)output_keys[max_idx]; } } } } } } //--- return(res); } //+------------------------------------------------------------------+ //| TestSampleTensorOutput | //+------------------------------------------------------------------+ bool TestSampleTensorOutput(long model,sIRISsample &iris_sample, int &model_class_id) { //--- model_class_id=-1; float input_data[1][4]; for(int k=0; k<4; k++) { input_data[0][k]=(float)iris_sample.features[k]; } //--- ulong input_shape[]= { 1, 4}; OnnxSetInputShape(model,0,input_shape); //--- int output1[1]; float output2[1,3]; //--- ulong output_shape[]= {1}; OnnxSetOutputShape(model,0,output_shape); //--- ulong output_shape2[]= {1,3}; OnnxSetOutputShape(model,1,output_shape2); //--- bool res=OnnxRun(model,0,input_data,output1,output2); //--- class for these models in output1[0]; if(res) model_class_id=output1[0]; //--- return(res); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ int OnStart(void) { sIRISsample iris_samples[]; //--- load dataset from file PrepareIrisDataset(iris_samples); //--- test int total_samples=ArraySize(iris_samples); if(total_samples==0) { Print("error in loading iris dataset from iris.csv"); return(false); } /*for(int k=0; k<total_samples; k++) { PrintFormat("%d (%.2f,%.2f,%.2f,%.2f) class %d (%s)",iris_samples[k].sample_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3],iris_samples[k].class_id,iris_samples[k].class_name); }*/ //---- string iris_models[]= { "random_forest_classifier_iris.onnx", "gradient_boosting_classifier_iris.onnx", "bagging_classifier_iris.onnx", "decision_tree_classifier_iris.onnx", "extra_tree_classifier_iris.onnx", "extra_trees_classifier_iris.onnx", "hist_gradient_boosting_classifier_iris.onnx", "logistic_regressioncv_classifier_iris.onnx", "mlp_classifier_iris.onnx", "linear_discriminant_analysis_classifier_iris.onnx", "svc_classifier_iris.onnx", "radius_neighbors_classifier_iris.onnx", "logistic_regression_classifier_iris.onnx", "nusvc_classifier_iris.onnx", "k-nn_classifier_iris.onnx", "linearsvc_classifier_iris.onnx", "adaboost_classifier_iris.onnx", "passive-aggressive_classifier_iris.onnx", "gaussian_naive_bayes_classifier_iris.onnx", "multinomial_naive_bayes_classifier_iris.onnx", "sgd_classifier_iris.onnx", "categorical_naive_bayes_classifier_iris.onnx", "ridge_classifier_iris.onnx", "ridge_classifiercv_iris.onnx", "complement_naive_bayes_classifier_iris.onnx", "perceptron_classifier_iris.onnx", "bernoulli_naive_bayes_classifier_iris.onnx" }; //--- test all iris dataset sample by sample for(int i=0; i<ArraySize(iris_models); i++) { //--- load ONNX-model string model_name="IRIS_models\\"+iris_models[i]; //--- long model=OnnxCreate(model_name,0); if(model==INVALID_HANDLE) { PrintFormat("model_name=%s OnnxCreate error %d for",model_name,GetLastError()); } else { //--- check all samples int correct_results=0; for(int k=0; k<total_samples; k++) { int model_class_id=-1; //--- select data output processor string current_model=iris_models[i]; if(current_model=="svc_classifier_iris.onnx" || current_model=="linearsvc_classifier_iris.onnx" || current_model=="nusvc_classifier_iris.onnx" || current_model=="ridge_classifier_iris.onnx" || current_model=="ridge_classifiercv_iris.onnx" || current_model=="radius_neighbors_classifier_iris.onnx") { TestSampleTensorOutput(model,iris_samples[k],model_class_id); } else { TestSampleSequenceMapOutput(model,iris_samples[k],model_class_id); } //--- if(model_class_id==iris_samples[k].class_id) { correct_results++; //PrintFormat("sample=%d OK [class=%d]",iris_samples[k].sample_id,model_class_id); } else { //PrintFormat("model:%s sample=%d FAILED [class=%d, true class=%d] features=(%.2f,%.2f,%.2f,%.2f]",model_name,iris_samples[k].sample_id,model_class_id,iris_samples[k].class_id,iris_samples[k].features[0],iris_samples[k].features[1],iris_samples[k].features[2],iris_samples[k].features[3]); } } PrintFormat("%d model:%s accuracy: %.4f",i+1,model_name,1.0*correct_results/total_samples); //--- release model OnnxRelease(model); } //--- } return(0); } //+------------------------------------------------------------------+
Sortie :
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
Comparaison avec les résultats du script 2.28.1.1 :
Python Random Forest Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Python Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Bagging Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Python Decision Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Tree Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Python Extra Trees Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Python Hist Gradient Boosting Classifier - Original Accuracy: 1.0000, ONNX Accuracy: 1.0000 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Python Logistic RegressionCV Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Python MLP Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Python Linear Discriminant Analysis Classifier - Original Accuracy: 0.9800, ONNX Accuracy: 0.9800 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Python SVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Python Radius Neighbors Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Python Logistic Regression Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Python NuSVC Classifier - Original Accuracy: 0.9733, ONNX Accuracy: 0.9733 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Python K-NN Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Python LinearSVC Classifier - Original Accuracy: 0.9667, ONNX Accuracy: 0.9667 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Python AdaBoost Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Python Passive-Aggressive Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Python Gaussian Naive Bayes Classifier - Original Accuracy: 0.9600, ONNX Accuracy: 0.9600 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Python Multinomial Naive Bayes Classifier - Original Accuracy: 0.9533, ONNX Accuracy: 0.9533 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Python SGD Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Python Categorical Naive Bayes Classifier - Original Accuracy: 0.9333, ONNX Accuracy: 0.9333 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Python Ridge Classifier - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Python Ridge ClassifierCV - Original Accuracy: 0.8533, ONNX Accuracy: 0.8533 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Python Complement Naive Bayes Classifier - Original Accuracy: 0.6667, ONNX Accuracy: 0.6667 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Python Perceptron Classifier - Original Accuracy: 0.6133, ONNX Accuracy: 0.6133 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Python Bernoulli Naive Bayes Classifier - Original Accuracy: 0.3333, ONNX Accuracy: 0.3333 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
il est intéressant de noter que l'exécution de tous les modèles ONNX sauvegardés dans MQL5 correspond tout à fait aux résultats de 2.28.1.
Les modèles que nous avons examinés, convertis au format ONNX, ont donc conservé leur précision de classification.
Il convient de mentionner que 7 modèles ont atteint une précision de classification parfaite (précision = 1,0) pour l'ensemble de données de l'iris :
- Classificateur Random Forest
- Classificateur Gradient Boosting
- Classificateur Bagging
- Classificateur Decision Tree
- Classificateur Extra Tree
- Classificateur Extra Trees
- Classificateur Histogram Gradient Boosting
Les 20 modèles restants ont commis des erreurs de classification.
Si vous décommentez la ligne 208, le script affichera également les échantillons du jeu de données de l'Iris qui ont été mal classés par chacun des modèles :
Iris_AllClassifiers (EURUSD,H1) 1 model:IRIS_models\random_forest_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 2 model:IRIS_models\gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 3 model:IRIS_models\bagging_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 4 model:IRIS_models\decision_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 5 model:IRIS_models\extra_tree_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 6 model:IRIS_models\extra_trees_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) 7 model:IRIS_models\hist_gradient_boosting_classifier_iris.onnx accuracy: 1.0000 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regressioncv_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 8 model:IRIS_models\logistic_regressioncv_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\mlp_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) 9 model:IRIS_models\mlp_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 10 model:IRIS_models\linear_discriminant_analysis_classifier_iris.onnx accuracy: 0.9800 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\svc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 11 model:IRIS_models\svc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\radius_neighbors_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 12 model:IRIS_models\radius_neighbors_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\logistic_regression_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) 13 model:IRIS_models\logistic_regression_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\nusvc_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) 14 model:IRIS_models\nusvc_classifier_iris.onnx accuracy: 0.9733 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\k-nn_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) 15 model:IRIS_models\k-nn_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\linearsvc_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 16 model:IRIS_models\linearsvc_classifier_iris.onnx accuracy: 0.9667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\adaboost_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 17 model:IRIS_models\adaboost_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\passive-aggressive_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 18 model:IRIS_models\passive-aggressive_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 19 model:IRIS_models\gaussian_naive_bayes_classifier_iris.onnx accuracy: 0.9600 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) 20 model:IRIS_models\multinomial_naive_bayes_classifier_iris.onnx accuracy: 0.9533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\sgd_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 21 model:IRIS_models\sgd_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) 22 model:IRIS_models\categorical_naive_bayes_classifier_iris.onnx accuracy: 0.9333 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 23 model:IRIS_models\ridge_classifier_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\ridge_classifiercv_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) 24 model:IRIS_models\ridge_classifiercv_iris.onnx accuracy: 0.8533 Iris_AllClassifiers (EURUSD,H1) ONNX: Removing initializer 'class_log_prior'. It is not used by any node and should be removed from the model. Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=2, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=2, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=2, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=2, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=2, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=2, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=2, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=2, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=2, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=2, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=2, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=2, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=2, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=2, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=2, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=2, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=2, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=2, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=2, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=2, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=2, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=2, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=2, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=2, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=2, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=2, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=2, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=2, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=2, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=2, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=2, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=2, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=2, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=2, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=2, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=2, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=2, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=2, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=2, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=2, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=2, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=2, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=2, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=2, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=2, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=2, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=2, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\complement_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=2, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) 25 model:IRIS_models\complement_naive_bayes_classifier_iris.onnx accuracy: 0.6667 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=2 FAILED [class=1, true class=0] features=(4.90,3.00,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=9 FAILED [class=1, true class=0] features=(4.40,2.90,1.40,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=10 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=13 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=21 FAILED [class=1, true class=0] features=(5.40,3.40,1.70,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=26 FAILED [class=1, true class=0] features=(5.00,3.00,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=31 FAILED [class=1, true class=0] features=(4.80,3.10,1.60,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=35 FAILED [class=1, true class=0] features=(4.90,3.10,1.50,0.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=42 FAILED [class=1, true class=0] features=(4.50,2.30,1.30,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=46 FAILED [class=1, true class=0] features=(4.80,3.00,1.40,0.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=102 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=103 FAILED [class=1, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=104 FAILED [class=1, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=105 FAILED [class=1, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=106 FAILED [class=1, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=107 FAILED [class=1, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=108 FAILED [class=1, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=109 FAILED [class=1, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=110 FAILED [class=1, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=111 FAILED [class=1, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=112 FAILED [class=1, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=113 FAILED [class=1, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=114 FAILED [class=1, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=116 FAILED [class=1, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=117 FAILED [class=1, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=118 FAILED [class=1, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=119 FAILED [class=1, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=120 FAILED [class=1, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=121 FAILED [class=1, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=122 FAILED [class=1, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=123 FAILED [class=1, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=124 FAILED [class=1, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=125 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=126 FAILED [class=1, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=127 FAILED [class=1, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=128 FAILED [class=1, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=129 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=130 FAILED [class=1, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=131 FAILED [class=1, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=132 FAILED [class=1, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=133 FAILED [class=1, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=134 FAILED [class=1, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=135 FAILED [class=1, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=136 FAILED [class=1, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=137 FAILED [class=1, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=138 FAILED [class=1, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=139 FAILED [class=1, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=140 FAILED [class=1, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=141 FAILED [class=1, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=142 FAILED [class=1, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=143 FAILED [class=1, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=144 FAILED [class=1, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=145 FAILED [class=1, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=146 FAILED [class=1, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=147 FAILED [class=1, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=148 FAILED [class=1, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=149 FAILED [class=1, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\perceptron_classifier_iris.onnx sample=150 FAILED [class=1, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 26 model:IRIS_models\perceptron_classifier_iris.onnx accuracy: 0.6133 Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=51 FAILED [class=0, true class=1] features=(7.00,3.20,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=52 FAILED [class=0, true class=1] features=(6.40,3.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=53 FAILED [class=0, true class=1] features=(6.90,3.10,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=54 FAILED [class=0, true class=1] features=(5.50,2.30,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=55 FAILED [class=0, true class=1] features=(6.50,2.80,4.60,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=56 FAILED [class=0, true class=1] features=(5.70,2.80,4.50,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=57 FAILED [class=0, true class=1] features=(6.30,3.30,4.70,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=58 FAILED [class=0, true class=1] features=(4.90,2.40,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=59 FAILED [class=0, true class=1] features=(6.60,2.90,4.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=60 FAILED [class=0, true class=1] features=(5.20,2.70,3.90,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=61 FAILED [class=0, true class=1] features=(5.00,2.00,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=62 FAILED [class=0, true class=1] features=(5.90,3.00,4.20,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=63 FAILED [class=0, true class=1] features=(6.00,2.20,4.00,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=64 FAILED [class=0, true class=1] features=(6.10,2.90,4.70,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=65 FAILED [class=0, true class=1] features=(5.60,2.90,3.60,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=66 FAILED [class=0, true class=1] features=(6.70,3.10,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=67 FAILED [class=0, true class=1] features=(5.60,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=68 FAILED [class=0, true class=1] features=(5.80,2.70,4.10,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=69 FAILED [class=0, true class=1] features=(6.20,2.20,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=70 FAILED [class=0, true class=1] features=(5.60,2.50,3.90,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=71 FAILED [class=0, true class=1] features=(5.90,3.20,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=72 FAILED [class=0, true class=1] features=(6.10,2.80,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=73 FAILED [class=0, true class=1] features=(6.30,2.50,4.90,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=74 FAILED [class=0, true class=1] features=(6.10,2.80,4.70,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=75 FAILED [class=0, true class=1] features=(6.40,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=76 FAILED [class=0, true class=1] features=(6.60,3.00,4.40,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=77 FAILED [class=0, true class=1] features=(6.80,2.80,4.80,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=78 FAILED [class=0, true class=1] features=(6.70,3.00,5.00,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=79 FAILED [class=0, true class=1] features=(6.00,2.90,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=80 FAILED [class=0, true class=1] features=(5.70,2.60,3.50,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=81 FAILED [class=0, true class=1] features=(5.50,2.40,3.80,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=82 FAILED [class=0, true class=1] features=(5.50,2.40,3.70,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=83 FAILED [class=0, true class=1] features=(5.80,2.70,3.90,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=84 FAILED [class=0, true class=1] features=(6.00,2.70,5.10,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=85 FAILED [class=0, true class=1] features=(5.40,3.00,4.50,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=86 FAILED [class=0, true class=1] features=(6.00,3.40,4.50,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=87 FAILED [class=0, true class=1] features=(6.70,3.10,4.70,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=88 FAILED [class=0, true class=1] features=(6.30,2.30,4.40,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=89 FAILED [class=0, true class=1] features=(5.60,3.00,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=90 FAILED [class=0, true class=1] features=(5.50,2.50,4.00,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=91 FAILED [class=0, true class=1] features=(5.50,2.60,4.40,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=92 FAILED [class=0, true class=1] features=(6.10,3.00,4.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=93 FAILED [class=0, true class=1] features=(5.80,2.60,4.00,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=94 FAILED [class=0, true class=1] features=(5.00,2.30,3.30,1.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=95 FAILED [class=0, true class=1] features=(5.60,2.70,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=96 FAILED [class=0, true class=1] features=(5.70,3.00,4.20,1.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=97 FAILED [class=0, true class=1] features=(5.70,2.90,4.20,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=98 FAILED [class=0, true class=1] features=(6.20,2.90,4.30,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=99 FAILED [class=0, true class=1] features=(5.10,2.50,3.00,1.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=100 FAILED [class=0, true class=1] features=(5.70,2.80,4.10,1.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=101 FAILED [class=0, true class=2] features=(6.30,3.30,6.00,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=102 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=103 FAILED [class=0, true class=2] features=(7.10,3.00,5.90,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=104 FAILED [class=0, true class=2] features=(6.30,2.90,5.60,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=105 FAILED [class=0, true class=2] features=(6.50,3.00,5.80,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=106 FAILED [class=0, true class=2] features=(7.60,3.00,6.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=107 FAILED [class=0, true class=2] features=(4.90,2.50,4.50,1.70] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=108 FAILED [class=0, true class=2] features=(7.30,2.90,6.30,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=109 FAILED [class=0, true class=2] features=(6.70,2.50,5.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=110 FAILED [class=0, true class=2] features=(7.20,3.60,6.10,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=111 FAILED [class=0, true class=2] features=(6.50,3.20,5.10,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=112 FAILED [class=0, true class=2] features=(6.40,2.70,5.30,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=113 FAILED [class=0, true class=2] features=(6.80,3.00,5.50,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=114 FAILED [class=0, true class=2] features=(5.70,2.50,5.00,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=115 FAILED [class=0, true class=2] features=(5.80,2.80,5.10,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=116 FAILED [class=0, true class=2] features=(6.40,3.20,5.30,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=117 FAILED [class=0, true class=2] features=(6.50,3.00,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=118 FAILED [class=0, true class=2] features=(7.70,3.80,6.70,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=119 FAILED [class=0, true class=2] features=(7.70,2.60,6.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=120 FAILED [class=0, true class=2] features=(6.00,2.20,5.00,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=121 FAILED [class=0, true class=2] features=(6.90,3.20,5.70,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=122 FAILED [class=0, true class=2] features=(5.60,2.80,4.90,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=123 FAILED [class=0, true class=2] features=(7.70,2.80,6.70,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=124 FAILED [class=0, true class=2] features=(6.30,2.70,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=125 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=126 FAILED [class=0, true class=2] features=(7.20,3.20,6.00,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=127 FAILED [class=0, true class=2] features=(6.20,2.80,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=128 FAILED [class=0, true class=2] features=(6.10,3.00,4.90,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=129 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=130 FAILED [class=0, true class=2] features=(7.20,3.00,5.80,1.60] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=131 FAILED [class=0, true class=2] features=(7.40,2.80,6.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=132 FAILED [class=0, true class=2] features=(7.90,3.80,6.40,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=133 FAILED [class=0, true class=2] features=(6.40,2.80,5.60,2.20] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=134 FAILED [class=0, true class=2] features=(6.30,2.80,5.10,1.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=135 FAILED [class=0, true class=2] features=(6.10,2.60,5.60,1.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=136 FAILED [class=0, true class=2] features=(7.70,3.00,6.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=137 FAILED [class=0, true class=2] features=(6.30,3.40,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=138 FAILED [class=0, true class=2] features=(6.40,3.10,5.50,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=139 FAILED [class=0, true class=2] features=(6.00,3.00,4.80,1.80] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=140 FAILED [class=0, true class=2] features=(6.90,3.10,5.40,2.10] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=141 FAILED [class=0, true class=2] features=(6.70,3.10,5.60,2.40] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=142 FAILED [class=0, true class=2] features=(6.90,3.10,5.10,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=143 FAILED [class=0, true class=2] features=(5.80,2.70,5.10,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=144 FAILED [class=0, true class=2] features=(6.80,3.20,5.90,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=145 FAILED [class=0, true class=2] features=(6.70,3.30,5.70,2.50] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=146 FAILED [class=0, true class=2] features=(6.70,3.00,5.20,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=147 FAILED [class=0, true class=2] features=(6.30,2.50,5.00,1.90] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=148 FAILED [class=0, true class=2] features=(6.50,3.00,5.20,2.00] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=149 FAILED [class=0, true class=2] features=(6.20,3.40,5.40,2.30] Iris_AllClassifiers (EURUSD,H1) model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx sample=150 FAILED [class=0, true class=2] features=(5.90,3.00,5.10,1.80] Iris_AllClassifiers (EURUSD,H1) 27 model:IRIS_models\bernoulli_naive_bayes_classifier_iris.onnx accuracy: 0.3333
2.29. Modèles de Classification dans Scikit-Learn qui n'ont pas pu être convertis en ONNX
Certains modèles de classification n'ont pas pu être convertis au format ONNX en raison d'erreurs dans le processus convert_sklearn.
2.29.1. DummyClassifier
DummyClassifier est un classificateur de la bibliothèque Scikit-learn utilisé comme modèle de base simple pour les tâches de classification. Il est conçu pour tester et évaluer les performances de modèles de classification plus complexes.
Principe de Fonctionnement :
Le DummyClassifier fonctionne de manière très simple : il fait des prédictions aléatoires ou naïves sans tenir compte des données d'entrée. Il propose différentes stratégies (sélectionnées par le paramètre "stratégie") :
- "most_frequent" (classe la plus fréquente) : Cette stratégie prédit toujours la classe qui apparaît le plus fréquemment dans l'ensemble de données d'apprentissage. Elle peut être utile dans les situations où les classes sont déséquilibrées et où vous devez prédire la classe dominante.
- "stratified" (choix stratifié) : Cette stratégie tente de faire des prédictions qui correspondent à la distribution des classes dans l'ensemble de données d'apprentissage. Il s'agit d'une méthode de sondage aléatoire qui prend en compte les proportions des classes.
- "uniform" (distribution uniforme) : Cette stratégie permet de faire des prédictions aléatoires avec une probabilité égale pour chaque classe. Elle est utile lorsque les classes sont équilibrées et que vous souhaitez tester les performances moyennes de votre modèle.
Capacités :
- Simplicité : DummyClassifier est utile pour tester la rapidité avec laquelle vous pouvez former un modèle de base et les résultats qu'il produit. Il peut être utile pour évaluer rapidement les performances d'autres classificateurs.
- Utilisation du Pipeline : Vous pouvez utiliser DummyClassifier comme modèle de base dans un pipeline, combiné à d'autres transformations et modèles à des fins de comparaison et de test.
Limites :
- N'utilise Pas les Données : Le classificateur fictif fait des prédictions aléatoires ou naïves sans tenir compte des données réelles. Il ne peut pas apprendre à partir des données ou découvrir des modèles.
- Inadaptés aux Tâches Complexes : Ce classificateur n'est pas conçu pour résoudre des tâches de classification complexes et ne donne généralement pas de bons résultats pour les tâches comportant de grands ensembles de données et des motifs complexes.
- Manque d'Information : Les résultats obtenus à l'aide de DummyClassifier peuvent manquer d'informations et ne pas fournir d'informations utiles sur les performances du modèle. Ils sont plus utiles pour le test et l’évaluation de code.
DummyClassifier est un outil utile pour les tests initiaux et l'évaluation des modèles de classification. Mais son utilisation est limitée dans les tâches complexes. Il ne peut pas remplacer des algorithmes de classification plus avancés.
2.29.1.1. Code pour Créer un Modèle de DummyClassifier
# Iris_DummyClassifier.py
# Le code démontre le processus d'entraînement du modèle DummyClassifier sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle DummyClassifier avec la stratégie "most_frequent"
dummy_classifier = DummyClassifier(strategy="most_frequent")
# entraîne le modèle sur l'ensemble des données
dummy_classifier.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = dummy_classifier.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of DummyClassifier model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "dummy_classifier_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin du modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of DummyClassifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of DummyClassifier model: 0.3333333333333333
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 0.33 1.00 0.50 50
Python 1 0.00 0.00 0.00 50
Python 2 0.00 0.00 0.00 50
Python
Python accuracy 0.33 150
Python macro avg 0.11 0.33 0.17 150
Python weighted avg 0.11 0.33 0.17 150
Python
Le modèle a été construit et exécuté avec succès dans Scikit-learn, mais des erreurs se sont produites lors de la conversion vers ONNX.
Dans l'onglet "Erreurs", les messages concernant les erreurs de conversion au format ONNX sont affichés :
onnx_model = convert_sklearn(dummy_classifier, initial_types=initial_type, target_opset=12) Iris_DummyClassifier.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyClassifier'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_DummyClassifier.py finished in 2071 ms 19 1
Par conséquent, le modèle DummyClassifier n'a pas pu être converti en ONNX.
2.29.2. Classificateur GaussianProcessClassifier
GaussianProcessClassifier est un classificateur qui utilise des processus gaussiens pour les tâches de classification. Il appartient à la famille des modèles qui utilisent des processus gaussiens. Il peut être utile dans les tâches où des estimations probabilistes des classes sont nécessaires.
Principe de Fonctionnement :
- GaussianProcessClassifier utilise un processus gaussien pour modéliser la correspondance entre l'espace des caractéristiques et l'espace des estimations de probabilité des classes.
- Il construit un modèle probabiliste pour chaque classe en évaluant la probabilité qu'un point appartienne à chaque classe.
- Lors de la classification, il sélectionne la classe dont la probabilité est la plus élevée pour un point donné.
Capacités :
- Classification Probabiliste : GaussianProcessClassifier fournit des estimations probabilistes des classes, qui peuvent être utiles pour évaluer l'incertitude du modèle.
- Capacité d'Adaptation : Ce classificateur peut s'adapter aux données et mettre à jour ses prédictions en fonction de nouvelles observations.
- Étalonnage : Le modèle peut être calibré à l'aide de la méthode "calibrate" pour améliorer les estimations de probabilité.
Limites :
- Complexité de Calcul : GaussianProcessClassifier peut s'avérer coûteux en termes de calcul pour les grands ensembles de données et/ou les espaces de caractéristiques à haute dimension.
- Ne Convient Pas pour les Grands Echantillons : En raison de sa complexité de calcul, ce classificateur peut ne pas être efficace pour l'apprentissage sur de grands ensembles de données.
- Complexité d'Interprétation : Les processus gaussiens peuvent être difficiles à interpréter et à comprendre, en particulier pour les utilisateurs qui n'ont pas d'expérience en matière de statistiques bayésiennes.
GaussianProcessClassifier est utile dans les tâches où les estimations probabilistes des classes sont importantes et où l'on peut supporter les coûts de calcul. Pour les tâches de classification sur de grands ensembles de données ou avec des structures de données simples, d'autres algorithmes de classification seront plus appropriés.
2.29.2.1. Code pour la Création d'un Modèle GaussianProcessClassifier# Iris_GaussianProcessClassifier.py
# Le code démontre le processus d'entraînement du modèle Iris_GaussianProcess Classifier sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle GaussianProcessClassifier avec un noyau RBF
kernel = 1.0 * RBF(1.0)
gpc_model = GaussianProcessClassifier(kernel=kernel)
# entraîne le modèle sur l'ensemble des données
gpc_model.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = gpc_model.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of GaussianProcessClassifier model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(gpc_model, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "gpc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin d'accès au modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of GaussianProcessClassifier model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of GaussianProcessClassifier model: 0.9866666666666667
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.98 0.98 50
Python 2 0.98 0.98 0.98 50
Python
Python accuracy 0.99 150
Python macro avg 0.99 0.99 0.99 150
Python weighted avg 0.99 0.99 0.99 150
Python
Dans l'onglet "Erreurs", les messages concernant les erreurs de conversion au format ONNX sont affichés :
onnx_model = convert_sklearn(gpc_model, initial_types=initial_type, target_opset=12) Iris_GaussianProcessClassifier.py 46 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is implemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is implemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_converter(operator, container, verbose=verbose) _topology.py 1349 1
conv(self.scopes[0], operator, container) _topology.py 1132 1
return self._fct(*args) _registration.py 27 1
raise NotImplementedError("Only binary classification is implemented.") gaussian_process.py 247 1
NotImplementedError: Only binary classification is implemented. gaussian_process.py 247 1
Iris_GaussianProcessClassifier.py finished in 4004 ms 9 1
Le modèle GaussianProcessClassifier n'a donc pas pu être converti en ONNX.
2.29.3. Classificateur LabelPropagation
LabelPropagation est une méthode d'apprentissage semi-supervisée utilisée pour les tâches de classification. L'idée principale de cette méthode est de propager les étiquettes (classes) des instances étiquetées aux instances non étiquetées dans une structure de données basée sur un graphe.
Le Processus de Propagation des Etiquettes (LabelPropagation) :
- Il commence par la construction d'un graphe où les nœuds représentent des instances de données et les arêtes entre les nœuds reflètent la similarité ou la proximité entre les instances.
- Attribution Initiale des Etiquettes : Les instances étiquetées reçoivent leur étiquette et les instances non étiquetées commencent avec une étiquette non définie.
- Propagation des étiquettes sur le graphique : Les étiquettes des instances étiquetées sont propagées aux instances non étiquetées sur la base de la similarité entre les instances. Cette similarité peut être déterminée de différentes manières, par exemple en utilisant les voisins les plus proches dans le graphe.
- Processus itératif : Les étiquettes peuvent changer au cours de plusieurs itérations, chaque itération mettant à jour les étiquettes des instances non étiquetées en fonction des étiquettes actuelles et de la similarité des instances.
- Stabilisation : Le processus se poursuit jusqu'à ce que les étiquettes se stabilisent ou qu'un certain critère d'arrêt soit rempli.
Avantages de LabelPropagation :
- Utilise des informations provenant de données non étiquetées : La méthode LabelPropagation permet d'utiliser des informations provenant d'instances non étiquetées afin d'améliorer la qualité de la classification. Cette méthode est particulièrement utile lorsque les données étiquetées sont rares.
- Robustesse au bruit : La méthode traite efficacement les données bruitées car elle prend en compte la similarité des instances et ne s'appuie pas uniquement sur les étiquettes.
Limites de LabelPropagation :
- Dépendance à l'égard du choix du graphique : La qualité de la classification par LabelPropagation peut dépendre fortement du choix du graphe et de la méthode de détermination de la similarité des instances. Des choix de paramètres incorrects peuvent conduire à des résultats médiocres.
- Complexité de calcul : En fonction de la taille et de la complexité des données, ainsi que des paramètres de la méthode, la méthode LabelPropagation peut nécessiter des ressources de calcul importantes.
- Potentiel de sur-ajustement : Si le graphique contient trop d'arêtes bruyantes ou d'étiquettes incorrectes, la méthode peut être sur-ajustée.
- La convergence n'est pas garantie : Dans de rares cas, LabelPropagation peut ne pas converger vers des étiquettes stables, ce qui nécessite de limiter le nombre d'itérations ou d'ajuster d'autres paramètres.
La méthode LabelPropagation est puissante, mais elle nécessite un réglage minutieux des paramètres et une analyse de la structure graphique des données pour obtenir de bons résultats.
2.29.3.1. Code de Création d'un Modèle LabelPropagationClassifier
# Iris_LabelPropagationClassifier.py
# Le code démontre le processus d'entraînement du modèle LabelPropagation Classifier sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.semi_supervised import LabelPropagation
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
from sys import argv
# définit le chemin d'accès pour l'enregistrement du modèle
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle LabelPropagation
lp_model = LabelPropagation()
# entraîne le modèle sur l'ensemble des données
lp_model.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = lp_model.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelPropagation model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "lp_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin d'accès au modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait la prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelPropagation model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of LabelPropagation model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Le modèle a été construit, mais des erreurs se sont produites lors de la conversion au format ONNX.
Dans l'onglet "Erreurs", les messages concernant les erreurs de conversion au format ONNX sont affichés :
onnx_model = convert_sklearn(lp_model, initial_types=initial_type, target_opset=12) Iris_LabelPropagation.py 44 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
Le modèle LabelSpreading Classifier n'a donc pas pu être converti en ONNX. onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelPropagation'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelPropagation.py finished in 2064 ms 19 1
2.29.4. Classificateur LabelSpreading
LabelSpreading est une méthode d'apprentissage semi-supervisée utilisée pour les tâches de classification. Elle repose sur l'idée de propager les étiquettes (classes) des instances étiquetées vers les instances non étiquetées dans une structure de données basée sur un graphe, similaire à LabelPropagation. Cependant, LabelSpreading inclut une stabilisation et une régularisation supplémentaires du processus de propagation des étiquettes.
Le Processus d’Étiquetage (LabelSpreading) :
- Il commence par la construction d'un graphe où les nœuds représentent des instances de données et les arêtes entre les nœuds reflètent la similarité ou la proximité entre les instances.
- Attribution Initiale des Etiquettes : Les instances étiquetées reçoivent leur étiquette et les instances non étiquetées commencent avec une étiquette non définie.
- Propagation des étiquettes sur le graphique : Les étiquettes des instances étiquetées sont propagées aux instances non étiquetées sur la base de la similarité entre les instances.
- Régularisation et stabilisation : LabelSpreading inclut une régularisation qui aide à stabiliser le processus de propagation des étiquettes et à réduire l'ajustement excessif. Pour cela, il faut tenir compte non seulement de la similarité entre les instances, mais aussi des différences entre les étiquettes des instances voisines.
- Processus itératif : Les étiquettes peuvent changer au cours de plusieurs itérations, où chaque itération met à jour les étiquettes sur les instances non étiquetées en fonction des étiquettes actuelles et de la régularisation.
- Stabilisation : Le processus se poursuit jusqu'à ce que les étiquettes se stabilisent ou qu'un certain critère d'arrêt soit rempli.
Avantages de LabelSpreading :
- Utilise des informations provenant de données non étiquetées : LabelSpreading permet d'utiliser des informations provenant d'instances non étiquetées pour améliorer la qualité de la classification.
- Régularisation : La présence d'une régularisation dans LabelSpreading permet de réduire le sur-ajustement et de rendre le processus de propagation des étiquettes plus stable.
Limites de LabelSpreading :
- Dépendance à l'égard du choix du graphique : Comme pour la méthode LabelPropagation, la qualité de la classification LabelSpreading peut dépendre fortement du choix du graphe et des paramètres de la méthode.
- Complexité de calcul : En fonction de la taille et de la complexité des données, ainsi que des paramètres de la méthode, LabelSpreading peut nécessiter des ressources de calcul importantes.
- Pas toujours convergent : Dans de rares cas, LabelSpreading peut ne pas converger vers des étiquettes stables, ce qui nécessite de limiter le nombre d'itérations ou d'ajuster d'autres paramètres.
LabelSpreading est une méthode qui nécessite également un réglage minutieux et peut constituer un outil puissant pour l'utilisation de données non étiquetées dans les tâches de classification.
2.29.4.1. Code pour la Création d'un Modèle LabelSpreadingClassifier
# Iris_LabelSpreadingClassifier.py
# Le code démontre le processus d'entraînement du modèle LabelSpreading Classifier sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.semi_supervised import LabelSpreading
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# récupère le chemin d'accès au script
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle LabelSpreading
ls_model = LabelSpreading()
# entraîne le modèle sur l'ensemble des données
ls_model.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = ls_model.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of LabelSpreading model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(ls_model, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "ls_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin d'accès au modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of LabelSpreading model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of LabelSpreading model: 1.0
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 1.00 1.00 1.00 50
Python 2 1.00 1.00 1.00 50
Python
Python accuracy 1.00 150
Python macro avg 1.00 1.00 1.00 150
Python weighted avg 1.00 1.00 1.00 150
Python
Dans l'onglet "Erreurs", les messages concernant les erreurs de conversion au format ONNX sont affichés :
onnx_model = convert_sklearn(ls_model, initial_types=initial_type, target_opset=12) Iris_LabelSpreading.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.semi_supervised._label_propagation.LabelSpreading'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_LabelSpreading.py finished in 2032 ms 19 1
Le modèle Classificateur LabelPropagation n'a pas pu être converti en ONNX.
2.29.5. Classificateur NearestCentroid
NearestCentroid est une méthode de classification basée sur l'idée de déterminer le centroïde de chaque classe et de classer les objets en fonction du centroïde le plus proche. Cette méthode est adaptée aux problèmes multi-classes et fonctionne bien sur les ensembles de données avec des classes linéairement séparables.
Le Processus NearestCentroid :
- Pour chaque classe, un centroïde est calculé, qui représente la valeur moyenne des caractéristiques de tous les objets appartenant à cette classe. Cela peut se faire en calculant la valeur moyenne de chaque caractéristique pour les objets de cette classe.
- Lors de la classification d'un nouvel objet, le centroïde le plus proche est calculé parmi les centroïdes de toutes les classes.
- Le nouvel objet est affecté à la classe dont le centroïde est le plus proche dans l'espace métrique.
Avantages de NearestCentroid :
- Simplicité et rapidité : La méthode NearestCentroid est simple à calculer et fonctionne rapidement sur de grands ensembles de données.
- Convient aux classes linéairement séparables : La méthode donne de bons résultats dans les tâches où les classes sont linéairement séparables ou proches de l'être.
- Efficace pour les problèmes multi-classes : NearestCentroid est adapté aux problèmes multi-classes et peut être utilisé comme classificateur de base dans les ensembles.
Limites de NearestCentroid :
- Sensibilité aux valeurs aberrantes : La méthode du plus proche centroïde est sensible aux valeurs aberrantes des données, car le centroïde peut être considérablement faussé par la présence de valeurs aberrantes.
- Biais spatial : Si les classes des données ont des variances et des formes différentes, la méthode du plus proche centroïde peut s'avérer moins efficace.
- Suppose l'égalité des moyens : Cette méthode suppose que les classes disposent d'un nombre à peu près égal de caractéristiques, ce qui n'est pas toujours le cas dans les données réelles.
- Ne convient pas aux tâches non linéaires : NearestCentroid n'est pas adapté aux tâches comportant des frontières non linéaires entre les classes.
NearestCentroid est une méthode de classification simple et interprétable qui peut s'avérer utile dans certains cas, notamment lorsque les classes sont linéairement séparables et qu'il n'y a pas de valeurs aberrantes dans les données.
2.29.5.1. Code pour la Création d'un Modèle NearestCentroid
# Iris_NearestCentroidClassifier.py
# Le code démontre le processus d'entraînement du modèle de Classification NearestCentroid sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.neighbors import NearestCentroid
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# récupère le chemin d'accès au script
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle NearestCentroid
nc_model = NearestCentroid()
# entraîne le modèle sur l'ensemble des données
nc_model.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = nc_model.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of NearestCentroid model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "nc_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin d'accès au modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of NearestCentroid model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of NearestCentroid model: 0.9266666666666666
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.87 0.92 0.89 50
Python 2 0.91 0.86 0.89 50
Python
Python accuracy 0.93 150
Python macro avg 0.93 0.93 0.93 150
Python weighted avg 0.93 0.93 0.93 150
Python
Dans l'onglet "Erreurs", les messages concernant les erreurs de conversion au format ONNX sont affichés :
onnx_model = convert_sklearn(nc_model, initial_types=initial_type, target_opset=12) Iris_NearestCentroid.py 45 1
onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
Le modèle Classificateur NearestCentroid n'a pas pu être converti en ONNX. onnx_model = convert_topology( convert.py 208 1
topology.convert_operators(container=container, verbose=verbose) _topology.py 1532 1
self.call_shape_calculator(operator) _topology.py 1348 1
operator.infer_types() _topology.py 1163 1
raise MissingShapeCalculator( _topology.py 629 1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.neighbors._nearest_centroid.NearestCentroid'>'. _topology.py 629 1
It usually means the pipeline being converted contains a _topology.py 629 1
transformer or a predictor with no corresponding converter _topology.py 629 1
implemented in sklearn-onnx. If the converted is implemented _topology.py 629 1
in another library, you need to register _topology.py 629 1
the converted so that it can be used by sklearn-onnx (function _topology.py 629 1
update_registered_converter). If the model is not yet covered _topology.py 629 1
by sklearn-onnx, you may raise an issue to _topology.py 629 1
https://github.com/onnx/sklearn-onnx/issues _topology.py 629 1
to get the converter implemented or even contribute to the _topology.py 629 1
project. If the model is a custom model, a new converter must _topology.py 629 1
be implemented. Examples can be found in the gallery. _topology.py 629 1
Iris_NearestCentroid.py finished in 2131 ms 19 1
2.29.6. Classificateur Quadratic Discriminant Analysis
L'Analyse Discriminante Quadratique, Quadratic Discriminant Analysis (QDA) est une méthode de classification qui utilise un modèle probabiliste pour séparer les données en classes. Il s'agit d'une généralisation de l'Analyse Discriminante Linéaire, Linear Discriminant Analysis (LDA) qui permet de prendre en compte les covariances des caractéristiques au sein de chaque classe. L'idée principale de la QDA est de modéliser la distribution des caractéristiques pour chaque classe, puis d'utiliser cette distribution pour classer de nouveaux objets.
Le Processus QDA :
- Les paramètres de la distribution sont calculés pour chaque classe, tels que la moyenne et la matrice de covariance des caractéristiques. Ces paramètres sont estimés sur la base des données d'apprentissage de chaque classe.
- En utilisant les paramètres obtenus, les densités de probabilité pour chaque classe peuvent être calculées à l'aide d'une distribution normale multivariée (ou d'une fonction de distribution quadratique).
- Lors de la classification d'un nouvel objet, les valeurs de densité de probabilité sont calculées pour chaque classe, et l'objet est affecté à la classe dont la probabilité est la plus élevée.
Avantages de la Quadratic Discriminant Analysis (QDA) :
- Prend en compte les covariances des caractéristiques : La QDA est plus flexible que la LDA car elle permet d'utiliser différentes matrices de covariance pour différentes classes, ce qui la rend plus adaptable à différentes structures de données.
- Convient aux frontières non linéaires : QDA est capable de modéliser des frontières complexes et non linéaires entre les classes.
- Robuste face aux données déséquilibrées : La méthode QDA peut donner de bons résultats pour les tâches dont les classes sont déséquilibrées.
Limites de l'Analyse Discriminante Quadratique (QDA) :
- Complexité de calcul : La QDA nécessite l'estimation de paramètres pour chaque classe, y compris des matrices de covariance, ce qui peut s'avérer coûteux en termes de calcul pour les grands ensembles de données.
- Données limitées : La méthode QDA peut s'avérer moins efficace lorsque les données sont limitées et que l'estimation des paramètres devient moins précise.
- Hypothèse d'une distribution normale : La QDA suppose que les données suivent une distribution normale, ce qui peut ne pas être le cas pour certains types de données.
- Risque de sur-ajustement : Si les données de formation sont insuffisantes ou si la covariance des caractéristiques est forte, la QDA peut être confrontée à des problèmes d'ajustement excessif.
L'Analyse Discriminante Quadratique (QDA) est une méthode de classification puissante adaptée à divers types de données et capable de prendre en compte les covariances des caractéristiques au sein des classes. Mais elle présente également des limites qu'il convient de prendre en compte lors de son utilisation.
2.29.6.1. Code pour la Création d'un Modèle Quadratic Discriminant Analysis
# Iris_QuadraticDiscriminantAnalysisClassifier.py
# Le code démontre le processus d'entraînement du modèle Classificateur Quadratic Discriminant Analysis sur le jeu de données Iris, son export au format ONNX, et la réalisation de prédictions à l'aide du modèle ONNX.
# Il évalue également la précision du modèle original et du modèle ONNX.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com
# importe les bibliothèques nécessaires
from sklearn import datasets
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.metrics import accuracy_score, classification_report
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
import onnxruntime as ort
import numpy as np
import sys
# récupère le chemin d'accès au script
script_path = sys.argv[0]
last_index = script_path.rfind("\\") + 1
data_path = script_path[0:last_index]
# charge l'ensemble de données Iris
iris = datasets.load_iris()
X = iris.data
y = iris.target
# crée un modèle QuadraticDiscriminantAnalysis
qda_model = QuadraticDiscriminantAnalysis()
# entraîne le modèle sur l'ensemble des données
qda_model.fit(X, y)
# prédit les classes pour l'ensemble du jeu de données
y_pred = qda_model.predict(X)
# évalue la précision du modèle
accuracy = accuracy_score(y, y_pred)
print("Accuracy of Quadratic Discriminant Analysis model:", accuracy)
# affiche le rapport de classification
print("\nClassification Report:\n", classification_report(y, y_pred))
# définit le type de données d'entrée
initial_type = [('float_input', FloatTensorType([None, X.shape[1]]))]
# exporte le modèle au format ONNX avec le type de données float
onnx_model = convert_sklearn(qda_model, initial_types=initial_type, target_opset=12)
# enregistre le modèle dans un fichier
onnx_filename = data_path + "qda_iris.onnx"
with open(onnx_filename, "wb") as f:
f.write(onnx_model.SerializeToString())
# affiche le chemin d'accès au modèle
print(f"Model saved to {onnx_filename}")
# charge le modèle ONNX et fait des prédictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
# affiche les informations sur les tenseurs d'entrée dans ONNX
print("\nInformation about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")
# affiche les informations sur les tenseurs de sortie dans ONNX
print("\nInformation about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")
# convertit les données au format virgule flottante (float32)
X_float32 = X.astype(np.float32)
# prédit les classes pour l'ensemble du jeu de données en utilisant ONNX
y_pred_onnx = onnx_session.run([output_name], {input_name: X_float32})[0]
# évalue la précision du modèle ONNX
accuracy_onnx = accuracy_score(y, y_pred_onnx)
print("\nAccuracy of Quadratic Discriminant Analysis model in ONNX format:", accuracy_onnx)
Sortie :
Python Accuracy of Quadratic Discriminant Analysis model: 0.98
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Python
Python Classification Report:
Python precision recall f1-score support
Python
Python 0 1.00 1.00 1.00 50
Python 1 0.98 0.96 0.97 50
Python 2 0.96 0.98 0.97 50
Python
Python accuracy 0.98 150
Python macro avg 0.98 0.98 0.98 150
Python weighted avg 0.98 0.98 0.98 150
Python
Python Model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx
Cette fois, le modèle a été sauvegardé avec succès au format ONNX. Mais lors de son exécution, des erreurs s'affichent dans l'onglet Erreurs :
onnx_session = ort.InferenceSession(onnx_filename) Iris_QuadraticDiscriminantAnalysisClassifier.py 55 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
self._create_inference_session(providers, provider_options, disabled_optimizers) onnxruntime_inference_collection.py 383 1
sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model) onnxruntime_inference_collection.py 424 1
onnxruntime.capi.onnxruntime_pybind11_state.InvalidGraph: [ONNXRuntimeError] : 10 : INVALID_GRAPH : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\qda_iris.onnx failed:This is an invalid mode onnxruntime_inference_collection.py 424 1
Iris_QuadraticDiscriminantAnalysisClassifier.py finished in 2063 ms 5 1
La conversion du modèle Classificateur Quadratic Discriminant Analysis en ONNX a rencontré une erreur.
Conclusions
Dans cette étude, nous avons mené des recherches sur 33 modèles de classification en utilisant l'ensemble de données Iris, en tirant parti de la bibliothèque Scikit-learn version 1.2.2.
1. Sur cet ensemble, 6 modèles ont rencontré des difficultés lors de leur conversion au format ONNX :
- DummyClassifier : Classificateur fictif
- GaussianProcessClassifier : Classificateur de Processus Gaussien
- LabelPropagation : Classificateur à Propagation d’Étiquettes
- LabelSpreading : Classificateur à Diffusion d’Étiquettes
- NearestCentroid : Classificateur du Centroïde Le Plus Proche
- QuadraticDiscriminantAnalysis : Classificateur d'Analyse Discriminante Quadratique
Il semble que ces modèles soient plus complexes en termes de structure et/ou de logique, et leur adaptation au format ONNX pourrait nécessiter des efforts supplémentaires. Il est également possible qu'ils utilisent des structures de données ou des algorithmes spécifiques qui ne sont pas entièrement pris en charge ou adaptés au format ONNX.
2. Les 27 modèles restants ont été convertis avec succès au format ONNX et ont démontré la préservation de leur précision. Cela met en évidence l'efficacité d'ONNX en tant qu'outil de sauvegarde et de restauration des modèles d'apprentissage automatique, permettant un transfert facile des modèles entre différents environnements et applications tout en maintenant leur performance.
La liste complète des modèles convertis avec succès au format ONNX comprend :
- SVC : Classificateur à Vecteur de Support
- LinearSVC : Classificateur à Vecteur de Support Linéaire
- NuSVC : Classificateur à Vecteur de Support Nu
- AdaBoostClassifier : Classificateur Adaptatif Boosting
- BaggingClassifier : Classificateur Agrégatif Bootstrap
- BernoulliNB : Classificateur Bernoulli Naive Bayes
- CategoricalNB : Classificateur Catégoriel Naive Bayes
- ComplementNB : Classificateur Complement Naive Bayes
- DecisionTreeClassifier : Classificateur Arbre de Décision
- ExtraTreeClassifier : Classificateur Extra Tree
- ExtraTreesClassifier : Classificateur Extra Trees
- GaussianNB : Classificateur Gaussian Naive Bayes
- GradientBoostingClassifier : Classificateur Gradient Boosting
- HistGradientBoostingClassifier : Classificateur de Renforcement du Gradient Basé sur l'Histogramme
- KNeighborsClassifier : Classificateur des Plus Proches Voisins (k-Nearest Neighbors)
- LinearDiscriminantAnalysis : Classificateur Linear Discriminant Analysis
- LogisticRegression : Classificateur Logistic Regression
- LogisticRegressionCV : Classificateur de Régression Logistique avec Validation Croisée
- MLPClassifier : Classification par Perceptron Multicouche
- MultinomialNB : Classificateur Multinomial Naive Bayes
- PassiveAggressiveClassifier : Classificateur Passif-Agressif
- Perceptron : Classificateur Perceptron
- RadiusNeighborsClassifier : Classificateur Radius Neighbors
- RandomForestClassifier : Classificateur Random Forest
- RidgeClassifier : Classificateur Ridge
- RidgeClassifierCV : Classificateur Ridge avec Validation Croisée
- SGDClassifier : Classificateur à Descente Stochastique de Gradient
3. De plus, au cours de la recherche, les modèles qui ont présenté des performances de classification exceptionnelles sur l'ensemble de données Iris ont été identifiés. Les modèles de classification tels que le Classificateur Random Forest, le Classificateur Gradient Boosting, le Classificateur Bagging, le Classificateur Decision Tree, le Classificateur Extra Tree, le Classificateur Extra Trees et le Classificateur Hist Gradient Boosting ont atteint une précision parfaite dans les prédictions. Cela signifie qu'ils peuvent déterminer avec précision la classe à laquelle appartient chaque échantillon d'iris.
Ces résultats peuvent être particulièrement utiles lors de la sélection du meilleur modèle pour des tâches de classification spécifiques. Les modèles qui ont atteint une précision parfaite sur les données Iris peuvent constituer un excellent choix pour les tâches impliquant l'analyse ou la classification de données similaires.
Cette recherche souligne ainsi l'importance de choisir le bon modèle pour des tâches spécifiques et met en évidence les avantages de l'utilisation d'ONNX pour préserver et appliquer des modèles d'apprentissage automatique pour des tâches de classification.
Conclusion
Dans cet article, nous avons analysé 33 modèles de classification en utilisant le jeu de données Iris avec Scikit-learn version 1.2.2.
Sur l'ensemble des modèles examinés, 6 se sont révélés difficiles à convertir au format ONNX. Ces modèles comprennent le Classificateur DummyClassifier, le Classificateur Gaussian Process, le Classificateur Label Propagation, le Classificateur Label Spreading, le Classificateur Nearest Centroid et le Classificateur Quadratic Discriminant Analysis. Leur structure ou leur logique complexe nécessite probablement une adaptation supplémentaire pour une conversion réussie au format ONNX.
Les 27 modèles restants ont été convertis avec succès au format ONNX et ont démontré la préservation de leur précision. Ceci réaffirme l'efficacité d'ONNX dans la préservation et la restauration des modèles d'apprentissage automatique, assurant la portabilité tout en maintenant la performance du modèle.
Certains modèles, tels que le Classificateur Random Forest, le Classificateur Gradient Boosting, le Classificateur Bagging, le Classificateur Decision Tree, le Classificateur Extra Tree, le Classificateur Extra Trees et le Classificateur Hist Gradient Boosting, ont notamment atteint une précision parfaite dans la classification des données Iris. Ces modèles peuvent être particulièrement intéressants pour les tâches où une grande précision est essentielle.
Cette recherche souligne l'importance de sélectionner le bon modèle pour des tâches spécifiques et démontre les avantages de l'utilisation d'ONNX pour préserver et appliquer des modèles d'apprentissage automatique dans des tâches de classification.
Tous les scripts de l'article sont également disponibles dans le projet public "MQL5\Projets partagés\Scikit.Classification.ONNX".
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/13451
Fichiers joints |
Scikit-learn-ClassificationModels-ONNX.zip
(220.05 KB)
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Aller à la discussion
Comment traiter les niveaux avec MQL5
Dans cet article, vous découvrirez comment traiter les lignes les plus importantes telles que les lignes de tendance, de support et de résistance avec MQL5.
Modèles de régression de la bibliothèque Scikit-learn et leur export vers ONNX
Dans cet article, nous allons explorer l'application des modèles de régression du paquet Scikit-learn, tenter de les convertir au format ONNX, et utiliser les modèles résultants dans des programmes MQL5. Nous comparerons également la précision des modèles originaux avec leurs versions ONNX pour la précision flottante et la précision double. Nous examinerons aussi la représentation ONNX des modèles de régression, afin de mieux comprendre leur structure interne et leurs principes opérationnels.
Apprenez à concevoir un système de trading à l'aide du Gator Oscillator
Un nouvel article de notre série sur l'apprentissage de la conception d'un système de trading basé sur des indicateurs techniques populaires sera consacré à l'indicateur technique Gator Oscillator et à la création d'un système de trading à l'aide de stratégies simples.
Combinatoire et théorie des probabilités pour le trading (Partie III) : Le premier modèle mathématique
Le développement de modèles mathématiques multifonctionnels pour les tâches de trading constituerait une suite logique du sujet abordé précédemment. Dans cet article, je décrirai l'ensemble du processus lié au développement du premier modèle mathématique décrivant les fractales, en partant de zéro. Ce modèle devrait devenir un élément de base important et être multifonctionnel et universel. Il permettra d'établir notre base théorique pour le développement ultérieur de cette idée.
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire