ケリー基準とモンテカルロシミュレーションを使用したポートフォリオリスクモデル
はじめに
数十年にわたり、トレーダーは破産リスクを最小限に抑えつつ長期的な資産成長を最大化する手法として、ケリー基準の公式を活用してきました。しかし、単一のバックテスト結果に基づいてケリー基準を盲目的に適用することは、個人トレーダーにとって非常に危険です。というのも、実際の取引では時間の経過とともに取引優位性が薄れ、過去の実績は将来の結果を保証するものではないからです。本記事では、Pythonによるモンテカルロシミュレーションの結果を取り入れ、MetaTrader 5上で1つ以上のエキスパートアドバイザー(EA)にケリー基準を現実的に適用するためのリスク配分アプローチを紹介します。
レバレッジ空間取引モデル理論
レバレッジ空間取引モデル(LSTM: Leverage Space Trading Model)は、主に金融市場および資産運用の分野で用いられる理論的枠組みです。このモデルは、借入資金を活用してリターンの増幅を図るレバレッジの概念と、市場の動態をより柔軟かつ空間的に捉えるモデリング手法とを統合しています。
LSTMでは、ケリー基準を用いて、単一の戦略における各取引に対して、ポートフォリオからリスクにさらすべき最適な割合を算出します。
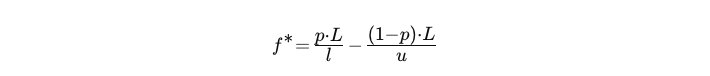
- L:レバレッジ係数
- p:成功の確率
- u:レバレッジ利得率
- l:レバレッジ損失率
バックテストの結果が与えられた場合、次の式で変数値を取得できます。

2:1のレバレッジで取引しているとします。次のように仮定します。
- 取引が成功する確率(p)=0.6(勝率60%)
- 期待収益(u)=0.1(レバレッジなしで10%の利益、レバレッジ2:1=20%の利益)
- 気体損失(l)=0.05(レバレッジなしで5%の損失、レバレッジ2:1=10%の損失)
ケリーの公式に代入します。
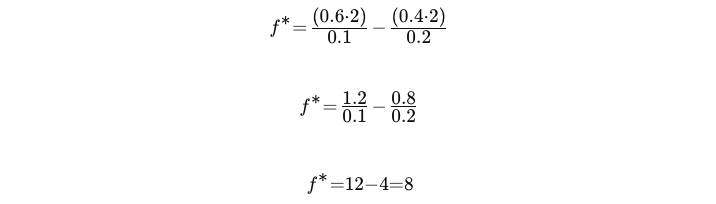
したがって、この取引でリスクを負う資本の最適な割合は、総資本の8%になります。
この式を自分のEAに適用すると、取引ごとにどれほどのリスクを取るべきだったのかが明確になり、必然的に不安を感じることでしょう。実際、この式は将来の結果がバックテストと同じレベルであると仮定していますが、これは現実的ではありません。そのため、業界では通常、リスクに分数ケリー基準を適用します。つまり、ケリー基準の値をある整数で割ってリスクを減らし、将来の不確実性に備えるのです。
ここで、トレーダーが安心してリスクを負いながら、取引ごとの期待収益を最大化するには、どの割合を選択すればよいかという疑問に答える必要があります。
Ralph Vince著の「The Leverage Space Trading Model」によると、確率的最適化プロセスを通じて、リターン期待関数は次元に関係なく凸型であることが明らかにされています。つまり、最適な期待収益には単一の解があり、f*の値が最適解から離れると期待値は連続的に減少するのです。
このことから、ライブ取引はバックテストほど理想的ではないため、実際のf*はケリー基準で計算されたf*よりも小さくなると予測されます。したがって、私たちがおこなうべきことは、ケリーリスクよりも小さいことを確認しつつ、許容できる最大レベルまでリスクを増加させることです。
通常、トレーダーの許容レベルは最大ドローダウンで測定されます。本記事では、合理的な許容レベルとして、最大ドローダウン30%を前提に進めます。
MQL5でのレバレッジリスクの適用
MQL5でレバレッジリスクを適用するには、まずリスクのパーセンテージをグローバル変数として宣言します。この場合、取引ごとに2%のリスクが発生します。
input double risk = 2.0;
次に、現在の価格単位でストップロスに基づいてロット量を計算する関数を記述します。たとえば、ストップロスが価格0に設定されている場合、ストップロスポイントは現在の価格に直接対応し、取引の結果は原資産の正確な動きを反映します。
//+------------------------------------------------------------------+ //| Calculate the corresponding lot size given the risk | //+------------------------------------------------------------------+ double calclots(double slpoints) { double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100; double ticksize = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_SIZE); double tickvalue = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE); double lotstep = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP); double moneyperlotstep = slpoints / ticksize * tickvalue * lotstep; double lots = MathFloor(riskAmount / moneyperlotstep) * lotstep; lots = MathMin(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MAX)); lots = MathMax(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MIN)); return lots; }
上記のコードでは、まず口座残高にリスク率を掛けてリスク額を決定します。
次に、銘柄のティックサイズ、ティック値、ロットステップを取得し、ストップロス距離に基づいて各ロットステップの金額を計算します。
ロットサイズは、リスク額をロットステップあたりの金額で割り、最も近いロットステップに丸めて決定されます。
最後に、計算されたロットサイズが銘柄の最小および最大許容ボリューム制限内であることを確認し、その結果を返します。
すべての取引戦略が固定のストップロスやテイクプロフィットを伴うわけではありませんが、レバレッジ取引の分野では、ケリー基準に基づき、取引を行う前にどれだけのリスクを取るかをあらかじめ決める必要があるため、固定のストップロスを使用していると仮定しています。
この関数は、実行をおこなう直前に呼び出します。例は次のようになります。
//+------------------------------------------------------------------+ //| Execute buy trade function | //+------------------------------------------------------------------+ void executeBuy(double price) { double sl = price- slp*_Point; sl = NormalizeDouble(sl, _Digits); double lots = lotpoint; if (risk > 0) lots = calclots(slp*_Point); trade.BuyStop(lots,price,_Symbol,sl,0,ORDER_TIME_DAY,1); buypos = trade.ResultOrder(); }通常、一貫して収益性の高いEAの場合、バックテストの結果は次のような指数関数に似たものになります。
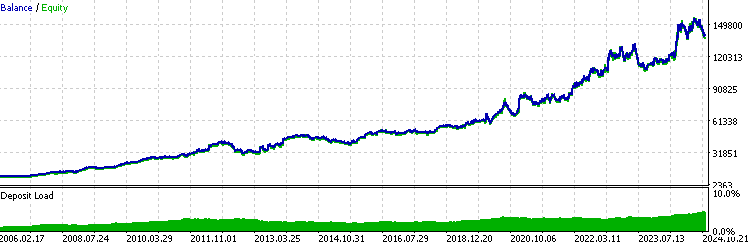
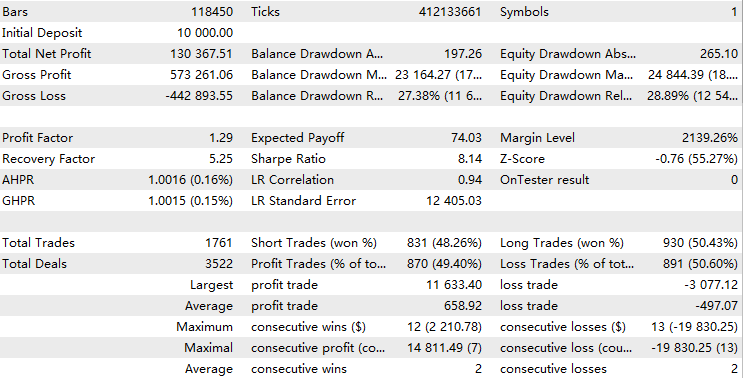
このレバレッジ取引モデルを使用するにあたって、バックテスト統計を分析する際に注意すべき点がいくつかあります。
- EAが一貫して利益を上げている場合、最近の結果が以前の結果よりも全体的なバックテストのパフォーマンスに与える影響が大きくなります。言い換えれば、最近のパフォーマンスに対してより重みを置いていることになります。
- LR相関は、グラフが指数曲線となるため、あまり役立ちません。
- シャープ比率は、リスクとリターンの間に線形関係があると仮定しているため、現実的ではありません。レバレッジは、潜在的なリターンとリスクの両方を増幅させるため、リスク調整後のパフォーマンス指標が歪む原因となります。
これらのメトリックを引き続き評価したい場合は、ロットサイズを固定し、再度テストを実行してください。
最大ドローダウンのモンテカルロシミュレーション
エクイティカーブは、口座残高のパーセンテージ変化の系列として表現され、最大ドローダウンはその中で累積パーセンテージが最も小さくなるセグメントとして定義されます。単一のバックテストは、この系列の中の1つの可能な配置に過ぎないため、その統計的な信頼性には限界があります。このセクションの目的は、発生する可能性のあるドローダウンを理解し、最大許容度の基準として95パーセンタイルを選択することです。
モンテカルロシミュレーションを使用すると、いくつかの方法で可能な株式曲線をシミュレートできます。
-
リターンのランダムサンプリング:過去のパフォーマンスや仮定された統計分布(例えば正規分布)に基づいてランダムなリターンを生成し、そのリターンを時間の経過とともに複利計算して、潜在的なエクイティカーブをシミュレートします。
-
ブートストラップ:過去のリターンを復元抽出(置き換えて再サンプリング)し、過去のパフォーマンスの変動性を反映する複数のシミュレートされたエクイティパスを生成します。
-
シャッフリング:過去のリターンの順序をランダムにシャッフルし、シャッフルされた系列を使用して異なるエクイティパスを生成することで、さまざまなシナリオを試すことができます。
-
リスク/リターン調整:指定したリスク基準(例:ボラティリティやドローダウン制限)に基づいて入力パラメータを変更し、さまざまな市場状況で現実的なエクイティカーブを生成します。
この記事では、シャッフリング方式に焦点を当てます。
まず、バックテストから取引レポートを取得するために、このように右クリックします。
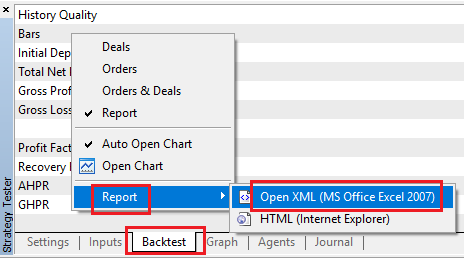
次に、Pythonを開き、このコードを使用して、各取引からの口座残高と損益を含む有用な行を抽出します。
import pandas as pd # Replace 'your_file.xlsx' with the path to your file input_file = 'DBG-XAU.xlsx' # Load the Excel file and skip the first {skiprows} rows data = pd.read_excel(input_file, skiprows=10757) # Select the 'profit' column (assumed to be 'Unnamed: 10') and filter rows as per your instructions profit_data = data[['Profit','Balance']][1:-1] profit_data = profit_data[profit_data.index % 2 == 0] # Filter for rows with odd indices profit_data = profit_data.reset_index(drop=True) # Reset index # Convert to float, then apply the condition to set values to 1 if > 0, otherwise to 0 profit_data = profit_data.apply(pd.to_numeric, errors='coerce').fillna(0) # Convert to float, replacing NaN with 0 # Save the processed data to a new CSV file with index output_csv_path = 'processed-DBG-XAU.csv' profit_data.to_csv(output_csv_path, index=True, header=['profit_loss','account_balance']) print(f"Processed data saved to {output_csv_path}")
スキップする行は基本的にこのインデックス-1より上の行です。
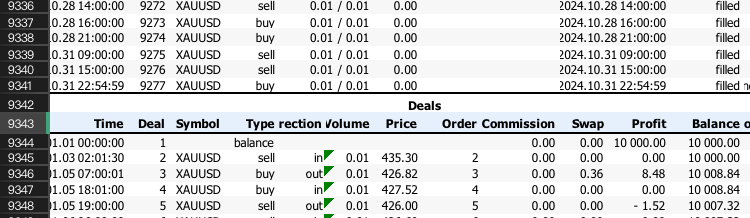
次に、リシャッフルされたシリーズが同じ最終残高になるように、各取引の利益をパーセンテージ変化に変換する必要があります。これは、口座残高の列を1行ずらし、各取引前の残高に対する利益または損失をパーセンテージで計算することによっておこないます。
initial_balance = account_balance.iloc[0] - profit_loss.iloc[0] # Calculate the account balance before each trade account_balance_before_trade = account_balance.shift(1) account_balance_before_trade.iloc[0] = initial_balance # Compute the percentage change made to the account balance for each trade percentage_change = profit_loss / account_balance_before_trade # Fill any NaN values that might have occurred percentage_change.fillna(0, inplace=True)
最後に、1000個のランダムなシリーズをシミュレートし、最大ドローダウンが最も大きい上位10個をプロットします。最終的なエクイティはすべて同じになることに注意してください。これは乗算の交換法則 によるものです。パーセンテージ変化の系列を乗算すると、値が並べ替えられる順序に関係なく、同じ結果が得られます。

最大ドローダウンの分布は正規分布に近いはずであり、ここで見ると95パーセンタイル(約2標準偏差)はおおよそ30%の最大ドローダウンとなっています。
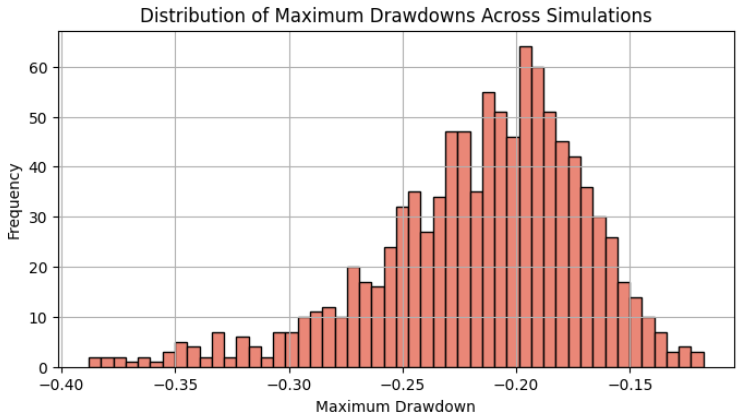
最初のバックテストでの最大ドローダウンはわずか17%で、この分布の平均値よりも小さいものでした。これを予想される最大ドローダウンとして採用していた場合、モンテカルロシミュレーションの結果を得た後、現在許容するリスクと比べてリスクが2倍に増加していたことになります。95%パーセンタイルを選んだ理由は、これが学者たちが実際の取引パフォーマンスに近いと考える一般的な結果だからです。幸運にも、95%パーセンタイルが当初設定した最大許容ドローダウンの30%とほぼ一致しました。つまり、ポートフォリオ内でこの単一のEAを取引する場合、1回の取引で2%のリスクを取ることで、最大許容範囲内で利益を最大化できることになります。もし結果が異なる場合は、最適な解を見つけるまでこの手順を繰り返す必要があります。
ポートフォリオ最適化のためのケリー基準
1つの口座で複数のEAを運用している場合、まず各EAについて上記の手順を完了し、最適なリスクを決定する必要があります。次に、そのリスクをポートフォリオ全体の中で各EAに割り当てられた資本に適用します。口座全体の観点から見ると、各EAのリスク額は、元々のリスクにそのEAに割り当てられた割合を乗じた値になります。
各EAのケリー配分率は、他のEAとのリターンの相関関係と、全体的なバックテストのパフォーマンスに基づいて決定されます。私たちの主な目的は、EA同士が互いのドローダウンを可能な限り相殺し、ポートフォリオ全体のエクイティカーブをより滑らかにすることです。EAや戦略を追加しても、相関関係がない場合にのみポートフォリオの多様性が強化されることに注意してください。相関関係が高い場合、単一のEAのリスクを増幅するのと同様に、ポートフォリオ全体のリスクが増加する可能性があります。
具体的には、次の式を使用して、期待リターンとリターンの共分散行列に基づいて、各戦略のケリー配分率を計算します。
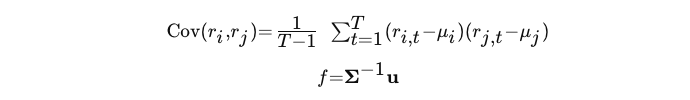
- r:時刻tにおけるEAiまたはEAjの戻り値
- μ:EAiまたはEAjの平均収益
- f:各EAのケリー配分
- Σ−1:共分散行列の逆行列
- u:各EAの期待収益のベクトル
上記の変数の値を抽出するためには、各戦略のバックテストを実行し、各戦略のパーセンテージリターンシリーズを1つのデータフレームに保存する必要があります。次に、すべてのEAの頻度に基づいて、リターンの相関が同一の時間期間内で計算されるため、記録に適した時間間隔を選択します。このような操作は次のPythonコードで実行します。
# Read returns for each strategy for file in strategy_files: try: data = pd.read_csv(file, index_col='Time') # Ensure 'Time' is parsed correctly as datetime data.index = pd.to_datetime(data.index, errors='coerce') # Drop rows where 'Time' or 'return' is invalid data.dropna(subset=['return'], inplace=True) # Aggregate duplicate time indices by mean (or could use 'sum', but here mean can ignore the trade frequency significance) data = data.groupby(data.index).agg({'return': 'mean'}) # Append results returns_list.append(data['return']) strategy_names.append(file) except Exception as e: print(f"Error processing {file}: {e}") continue # Check if any data was successfully loaded if not returns_list: print("No valid data found in files.") return # Combine returns into a single DataFrame, aligning by date returns_df = pd.concat(returns_list, axis=1, keys=strategy_names) # Uncomment the below line if u wanna drop rows with missing values across strategies #returns_df.dropna(inplace=True) #Uncomment the below line if u wanna just fill unaligned rows with 0( I think this is best for backtest that may have years differences) returns_df.fillna(0, inplace=True)
すべてのバックテスト結果が同時に開始および終了することを確認します。さらに、結果を集計するための適切な時間間隔を選択し、取引数が多すぎる期間や、取引がまったくない期間がないようにする必要があります。時間間隔があまりにも離散的すぎると、共分散を正確に計算するために同じ時間範囲内のデータポイントが不十分になる可能性があります。私たちの場合、1か月の間隔を選択し、各月の平均リターンをリターン特徴量として使用します。
次に計算をおこないます。
# Calculate expected returns (mean returns) expected_returns = returns_df.mean() # Calculate the covariance matrix of returns cov_matrix = returns_df.cov() # Compute the inverse of the covariance matrix try: inv_cov_matrix = np.linalg.inv(cov_matrix.values) except np.linalg.LinAlgError: # Use pseudo-inverse if covariance matrix is singular inv_cov_matrix = np.linalg.pinv(cov_matrix.values) # Calculate Kelly optimal fractions kelly_fractions = inv_cov_matrix @ expected_returns.values kelly_fractions = kelly_fractions / np.sum(kelly_fractions)
最終的には、次のような出力になります。
Strategy Kelly Fraction 0 A1-DBG-XAU.csv 0.211095 1 A1-DBG-SP.csv 0.682924 2 A1-DBG-EU.csv 0.105981
初期のリスク計算はすでに口座残高の合計に基づいていたため、このリスクを元のMQL5コードに直接実装できます。口座残高が変動するたびに、割り当てられた資本は自動的に再計算され、次の取引に適用されます。
double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;
たとえば、計算されたケリー分数をサンプルEAに適用するには、元のコードのこの部分を変更するだけで済みます。
input double risk = 2.0*0.211095;
各EAに割り当てられた資本の変化に基づいてリスクを再計算することもできることは十分承知していますが、次の理由からポートフォリオ全体に基づいて計算する方が望ましいです。
- 私の意見では、複数の口座を開設するか、取引ごとに変更を更新するためのプログラムを作成する必要があるため、各EAに割り当てられた資本の変化を追跡するのは実用的ではありません。
- ケリー基準は、ポートフォリオ全体の長期的な成長を最大化するために使用されます。個々のEAのパフォーマンスは他のEAのリスクに影響を与え、ポートフォリオが拡大する際に効率的な成長が促進されます。
- リスクを各EAに割り当てられた資本の変化に基づいて計算すると、パフォーマンスが良好なEAでは時間の経過とともに割り当てられた資本が増加し、そのEAのリスクエクスポージャーも増加します。これでは、相関関係に基づいてリスク配分を計算するという当初の意図を損なうことになります。
ただし、私たちのアプローチには一定の制限もあります。
- 各EAのリスクはポートフォリオ全体のパフォーマンスに応じて変動します。そのため、個々のEAのパフォーマンスを追跡するのは困難です。ポートフォリオ全体はS&P500のようなインデックスとして扱えますが、個々のパフォーマンスを評価するには絶対的な利益ではなく、パーセンテージの変化を計算する必要があります。
- 私たちのリスク配分計算では、各EAの取引頻度は考慮されていません。したがって、同じ口座で取引頻度が大きく異なるEAがある場合、割り当てが適切であってもリスク露出が不均一になる可能性があります。
全体的には、個々のトレーダーの成長を最大化するためには、このアプローチを採用する価値があると考えています。
結論
この記事では、レバレッジスペース取引モデルの文脈におけるケリー基準と、その取引への応用について紹介しました。次に、MQL5での実装コードを提供しました。続いて、モンテカルロシミュレーションを使用して、単一のバックテストに基づいて考慮すべき最適な最大ドローダウンを決定し、それを個々のEAのリスク評価に適用しました。最後に、バックテストのパフォーマンスと相関関係に基づいて、各EAに資本を配分するアプローチを提示しました。
ファイルテーブル
| 名前 | 使用法 |
|---|---|
| KellyMultiFactors.ipynb | 資本配分のためのケリー分数を計算する |
| MonteCarloDrawdown.ipynb | モンテカルロシミュレーションを実行する |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/16500
 MQL5入門(第10回):MQL5の組み込みインジケーターの操作に関する初心者向けガイド
MQL5入門(第10回):MQL5の組み込みインジケーターの操作に関する初心者向けガイド
 MQL5経済指標カレンダーを使った取引(第5回):レスポンシブコントロールとフィルターボタンでダッシュボードを強化する
MQL5経済指標カレンダーを使った取引(第5回):レスポンシブコントロールとフィルターボタンでダッシュボードを強化する
 MQL5取引ツールキット(第4回):履歴管理EX5ライブラリの開発
MQL5取引ツールキット(第4回):履歴管理EX5ライブラリの開発
 CatBoost機械学習モデルをトレンド追従戦略のフィルターとして活用する
CatBoost機械学習モデルをトレンド追従戦略のフィルターとして活用する
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索