人工藻类算法（Artificial Algae Algorithm，AAA）

内容

1. 概述
2. 算法实现
3. 测试结果

概述

藻类是地球上最古老的生物之一，在水生生态系统中发挥着关键的作用。藻类有超过45,000种，它们在颜色、形状、大小和栖息地方面可能差异很大。它们为水生环境赋予了生机，因为它们是许多动物物种的食物基础，并且它们通过光合作用产生氧气，对维持地球上的生命至关重要。这些生物可以是单细胞的或多细胞的，并且常常作为一个整体运作的群体。

单细胞藻类可以通过有丝分裂进行分裂，形成的新细胞仍然相互连接，从而形成一个群体。多细胞藻类可以通过孢子繁殖，这些孢子在水中传播并萌发成新的生物体，同样形成群体。这些令人惊叹的生物展示了如何利用生物过程来创造数学建模和优化中的创新解决方案。

人工藻类算法（AAA）由Uymaz、Tezel和Yel于2015年提出，是生物自然现象与数学思维的结合。这种元启发式优化算法的灵感来源于藻类微生物的迷人世界，其群体习性和适应能力是创建算法优化模型的基础。受藻类微生物向光源移动、适应变化的环境条件以及通过有丝分裂繁殖以改善光合作用能力的启发，从而开发了以数学方式模拟这些独特属性的AAA。

该算法包括三个关键过程：螺旋运动、进化过程和适应性。螺旋运动模拟藻类在营养液中的三维运动，使它们能够找到最佳的生长条件。进化过程确保藻类群体在最适合的条件下繁殖，从而促进生长并改进解决方案。适应性帮助不太成功的群体变得更像最大的群体，确保它们的生存和进一步发展。

算法实现

开发人工藻类算法（Artificial Algae Algorithm，AAA）用来对藻类的属性进行数学建模，例如它们的螺旋运动、适应性和进化过程。每个藻类群体代表优化问题的一个可能的候选解（群体中的每个细胞都是一个独立的坐标），这些群体组合形成一个藻类种群。每个群体以其大小为特征，这反映了所呈现解决方案的质量。

在进化过程中，获得更适宜环境条件的藻类群体才能发展和生长。无法获得适宜条件的群体则不会发展甚至死亡。螺旋运动完成后，藻类群体根据其尺寸大小进行排名。从最大的群体中随机选择的一个细胞复制到最小群体的相同细胞中，从而完成进化过程。

藻类群体在水中进行螺旋运动，以获得更好的环境条件。它们的能量与群体大小成正比。在运动过程中，它们会失去能量，但如果它们到达一个更好的环境，它们会恢复一半失去的能量。群体的能量与营养物质浓度直接成正比，因此群体的能量越多，其运动频率越高。

摩擦力是另一个影响水中运动的重要因素。表面积较小的群体由于其摩擦表面较小，因此具有更大的运动范围。达到更好条件的群体由于其大小而具有更大的摩擦表面积，因此群体减慢其运动，这有助于它们探索找到解决方案的周围区域并增强其局部搜索能力。

适应性发生在螺旋运动期间未获得足够发展的藻类群体试图模仿最大群体时。饥饿值最高的群体将经历这一过程。在优化开始时，所有群体的饥饿值均为零。在螺旋运动期间，未找到更好解决方案的群体的饥饿值增加1。螺旋运动和进化过程之后，饥饿值最高的群体进入适应期。然而，适应过程并非在每次迭代中都发生。首先，选择一个介于0和1之间的随机值。如果该值小于适应参数，则执行适应。

让我们继续编写AAA伪代码：

列出算法中使用的方程。方程1-5直接关联到算法基本逻辑的实现。

1. 种群初始化：种群 = [[x1_1, x1_2, ..., x1_D], [x2_1, x2_2, ..., x2_D], [xN_1, xN_2, ..., xN_D]]，其中 xj_i — i是第 j 个藻类菌落的细胞，D — 菌落维度，N — 种群大小。

2. 螺旋运动：x'i_j = xi_j + α * cos (θ) * τ (Xi) * p；y'i_j = yi_j + α * sin (θ) * τ (Xi) * p；z'i_j = zi_j + r * v，其中 (x'i_j, y'i_j, z'i_j) — 第 i 个菌落的新坐标，α，θ ∈ [0, 2π]，p ∈ [-1, 1]，r ∈ [-1, 1]，v ∈ [-1, 1]，τ (Xi) — 第 i 个菌落的摩擦区域。

3. 进化过程：biggest = max (Gi)，m = 随机选择的细胞，smallest.xm = biggest.xm

4. 适应性：starving = max (Ai)；starving.x = starving.x + (biggest.x - starving.x) * rand

5. 藻类生长的Monod模型：μt = μtmax * St / (St + Kt)，其中 μt 是在给定时间 t 下藻类的生长速率，μtmax 是最大生长速率，St — 在给定时间 t 内的菌落尺寸大小，Kt 是半饱和常数。

6. 摩擦区域：τ (Xi) = 2π * (3√ (3*Gi) / (4π))^2，其中 τ (Xi) 是第 i 个菌落的摩擦区域，Gi 是第 i 个菌落的大小。

7. 用于螺旋运动的菌落选择：使用竞争式选择法来选择将要移动的菌落。我们将在后面更详细地讨论这一点。

8. 为螺旋运动选择随机维度：p，r，v 是 随机选择的测量指标，它们彼此不同。

9. 为螺旋运动选择邻近菌落：Xj 是通过竞争式选择法选出的菌落，Xi 菌落将向其移动。

10. 所有菌落的初始饥饿度：Ai = 0 对于所有 i。

11. 无优化解的菌落饥饿度增加：如果菌落没有找到更好的解，则 Ai = Ai + 1。

12. 选择饥饿度最大的菌落：starving = max (Ai)。

13. 适应概率：rand < Ap，其中 Ap 是适应参数。

方程 6-13 描述了算法实现的更多细节，例如摩擦区域的计算、用于移动的菌落选择、菌落饥饿度的管理以及适应性概率。

Monod模型 经常被用来描述生物系统中种群的增长和行为。它基于法国生物化学家雅克·莫诺德（Jacques Monod）的研究，他研究了微生物的生长动力学。种群的增长速率取决于底物（营养物）的浓度。在底物浓度较低时，生长速率与浓度成正比；而在高浓度时，生长速率达到最大值。在优化算法中，Monod 模型被用来模拟进化算法中种群的增长和适应。在优化过程中，种群参数会根据可用资源的变化而改变，这使得对真实生物过程的建模更加准确。

我想请您注意用于选择菌落的竞争式选择法。我们以前在算法中没有使用过这种方法。让我们编写一个脚本并打印出结果，以便清楚地看到使用这种选择方法时种群中个体被选择的概率分布。用 蓝色 标记的代码段直接表示选择过程中形成的分布。

input int      PopSize = 50;
input int      Count   = 1000000;
input int      BarWidth = 50; // Histogram width in characters

void OnStart()
{
  int pop[];
  ArrayResize(pop, PopSize);

  for(int i = 0; i < PopSize; i++) pop[i] = PopSize - i;

  Print("Original population:");
  ArrayPrint(pop);

  int tur[];
  ArrayResize(tur, PopSize);
  ArrayInitialize(tur, 0);

  int ind1 = 0, ind2 = 0;

  for(int i = 0; i < Count; i++)
  {
    ind1 = MathRand() % PopSize;
    ind2 = MathRand() % PopSize;

    if(pop[ind1] > pop[ind2]) tur[ind1]++;
    else                      tur[ind2]++;
  }

  Print("Probability distribution (in %):");

  double maxPercentage = 0;
  double percentages[];
  ArrayResize(percentages, PopSize);

  for(int i = 0; i < PopSize; i++)
  {
    percentages[i] = (double)tur[i] / Count * 100;
    if(percentages[i] > maxPercentage) maxPercentage = percentages[i];
  }

  for(int i = 0; i < PopSize; i++)
  {
    int barLength = (int)((percentages[i] / maxPercentage) * BarWidth);
    string bar = "";
    for(int j = 0; j < barLength; j++) bar += "|";

    PrintFormat("%2d: %5.2f%% %s", i, percentages[i], bar);
  }
}

以下是运行脚本后，可视化选择种群中每个个体的概率分布结果：

概率分布呈线性下降，使得具有更高获得优化解机会的菌落能够被选中，但效率较低的菌群也有被选中的机会。这种选择方法并不依赖于个体适应度的绝对值，从而提供了广泛的解的多样性。

在之前的文章中，我们已经考虑过在选择过程中改变概率分布的函数，但这些函数能够提供概率的线性和非线性下降，并且计算成本更低（对于竞争式选择，需要两次调用 MathRand() 函数）。

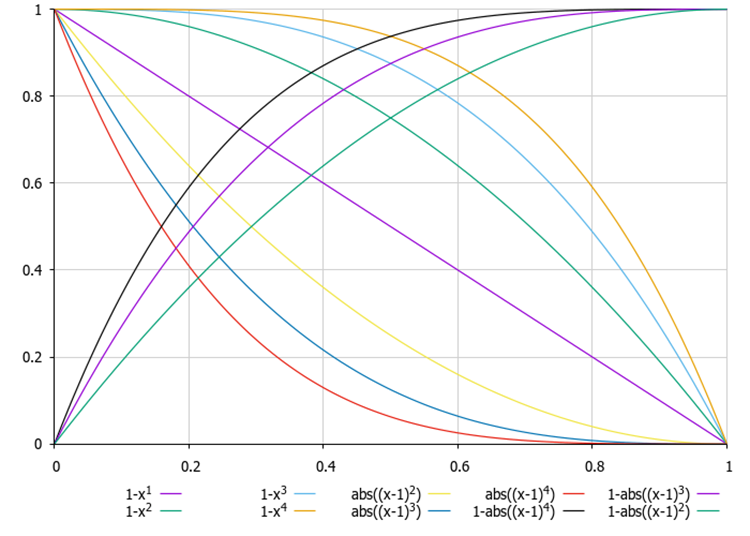
图例1. 改变概率分布形状的函数实例，其中 x 是在[0.0,1.0] 范围内均匀分布的随机数。

现在我们已经详细地了解了算法的所有细节，可以开始编写代码。

让我们描述一下 S_AAA_Agent 结构，该结构将用于在算法中模拟藻类菌落（智能体）。该结构包含四个字段：

• energy —— 智能体的能量水平。
• hunger — 智能体的饥饿水平。
• size — 智能体的尺寸大小（藻类的高度和长度）。
  
• friction — 影响智能体移动的摩擦比。

Init — 该方法用默认值初始化结构成员。 

因此，S_AAA_Agent 结构是一个具有基本特征的简单智能体模型。

//——————————————————————————————————————————————————————————————————————————————
struct S_AAA_Agent
{
  double energy;
  int    hunger;
  double size;
  double friction;

  void Init ()
  {
    energy   = 1.0;
    hunger   = 0;
    size     = 1.0;
    friction = 0.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

让我们编写从 C_AO 基类继承的 C_AO_AAA 类的定义。这意味着它将继承基类的所有成员和方法，并且可以进行扩展或覆盖。

1. 在类的构造函数中，为与算法相关的各种参数设置值，并且还需要初始化：

• popSize — 种群规模。
• adaptationProbability — 适应概率。
• energyLoss — 能量损失。
• maxGrowthRate — 最大生长速率。
• halfSaturationConstant — 半饱和常数。

所有这些参数都存储于 params 数组中。

2. SetParams 方法从 params 数组中更新算法参数的值。

3. 可用的选项有：

• Init() — 初始化方法，包括最小和最大参数值的数组，以及步长和迭代次数。
• Moving() —负责移动或更新智能体状态的方法。
• Revision() — 用于审核或评估状态的方法。
• EvolutionProcess()，AdaptationProcess()，CalculateEnergy()，TournamentSelection() — 这些私有方法分别负责进化过程、适应过程、藻类能量的计算以及竞争式选择。
  

类字段：

• adaptationProbability，energyLoss，maxGrowthRate，halfSaturationConstant — 用于存储参数值的变量。
• S_AAA_Agent agent[] — 智能体数组。
  
• fMin，fMax —种群的健壮度值（藻类大小）。

C_AO_AAA 类是一个结构，便于管理参数和智能体的状态，并且通过从 C_AO 类继承，能够集成到更广泛的系统中。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_AAA : public C_AO
{
  public: //--------------------------------------------------------------------

  ~C_AO_AAA () { }

  C_AO_AAA ()
  {
    ao_name = "AAA";
    ao_desc = "Algae Adaptive Algorithm";
    ao_link = "https://www.mql5.com/en/articles/15565";

    popSize                = 200;
    adaptationProbability  = 0.2;
    energyLoss             = 0.05;
    maxGrowthRate          = 0.1;
    halfSaturationConstant = 1.0;

    ArrayResize (params, 5);

    params [0].name = "popSize";                params [0].val = popSize;
    params [1].name = "adaptationProbability";  params [1].val = adaptationProbability;
    params [2].name = "energyLoss";             params [2].val = energyLoss;
    params [3].name = "maxGrowthRate";          params [3].val = maxGrowthRate;
    params [4].name = "halfSaturationConstant"; params [4].val = halfSaturationConstant;
  }

  void SetParams ()
  {
    popSize                = (int)params [0].val;
    adaptationProbability  = params      [1].val;
    energyLoss             = params      [2].val;
    maxGrowthRate          = params      [3].val;
    halfSaturationConstant = params      [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double adaptationProbability;
  double energyLoss;
  double maxGrowthRate;
  double halfSaturationConstant;

  S_AAA_Agent agent [];

  private: //-------------------------------------------------------------------
  void   EvolutionProcess    ();
  void   AdaptationProcess   ();
  double CalculateEnergy     (int index);
  int    TournamentSelection ();
  double fMin, fMax;
};
//——————————————————————————————————————————————————————————————————————————————

让我们详细看一下 C_AO_AAA 类的 Init 方法：

• rangeMinP — 每个参数的最小值数组。
• rangeMaxP — 每个参数的最大值数组。
• rangeStepP — 每个参数的变化步长数组。
• epochsP — 迭代次数（默认值为 0）。

方法字段：

1. StandardInit 方法使用传递的参数执行标准初始化。 

2. 将 agent 数组的大小更改为 popSize。这使我们能够为智能体存储一个数组。

3. 设置运行期间使用函数的最小值和最大值。

4. 循环遍历每个智能体，使用 Init 方法对其初始化。

5. 内层循环初始化每个智能体的坐标：

• 首先，使用 RNDfromCI 方法在 rangeMin[c] 到 rangeMax[c] 范围内随机设置 c 坐标。
• 接下来，使用 SeInDiSp 更改坐标，并对值进行归一化。

如果所有操作都成功，该方法返回true。因此，Init 方法使用给定的范围和步长初始化智能体数组的坐标。包括标准初始化、设置函数的边界以及随机分配坐标值。

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_AAA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  ArrayResize (agent, popSize);

  fMin = -DBL_MAX;
  fMax =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    agent [i].Init ();

    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

让我们看一下 C_AO_AAA 类的 Moving 方法的代码。总体结构和功能如下：

1. 如果变量 revision 为 false，则将其设置为 true，并且函数终止。这意味着在第一次迭代中不会执行 Moving 方法的基本逻辑。

2. 循环遍历所有 popSize 个种群元素。

3. 在 TournamentSelection 函数中执行竞争式选择，该函数返回一个智能体（藻类）的索引，以便后续使用。

4. 内层循环遍历每个坐标（由 coords 变量指定的空间维度）。

5. 使用 u.RNDfromCI 方法生成三个随机值：α 和 β（角度）以及 ρ（在 -1 到 1 之间的值）。

6. 根据 variant 的值（从 0 到 2 变化），更新 a[i].c[c] 坐标：

• 如果 variant 为 0，则使用 α 角的余弦值。
• 如果 variant 为 1，则使用 β 角的正弦值。
• 如果 variant 为 2，则使用 ρ 的值。

使用 variant 变量可以模拟藻类在多维空间中的三维螺旋运动。通过指定 agent[i].friction 摩擦力更新坐标。

7. 使用 u.SeInDiSp 函数限制 a[i].c[c] 坐标，该函数在给定范围内以给定步长设置值。

Moving 函数通过基于智能体的当前状态和其他智能体的状态，通过随机更改智能体的坐标来实现该过程。使用摩擦力和随机值可以创建动态，从而模拟智能体在搜索空间中的行为。代码包括防止超出指定范围的机制，这对于保持有效的坐标值很重要。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    int variant = 0;

    int j = TournamentSelection ();

    for (int c = 0; c < coords; c++)
    {
      double α = u.RNDfromCI (0.0, 2 * M_PI);
      double β = u.RNDfromCI (0.0, 2 * M_PI);
      double ρ = u.RNDfromCI (-1.0, 1.0);

      if (variant == 0) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathCos (α);
      if (variant == 1) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * MathSin (β);
      if (variant == 2) a [i].c [c] += (a [j].c [c] - a [i].c [c]) * agent [i].friction * ρ;

      variant++;

      if (variant > 2) variant = 0;

      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

在 Moving 方法之后，轮到 C_AO_AAA 类的 Revision 方法。该方法负责根据智能体的特征和相互作用来更新种群中智能体的状态。总体结构如下：

1. 将ind变量初始化为-1。它将用于存储具有最佳函数值的智能体的索引。

2. 循环遍历 popSize 种群中的所有智能体。在循环中：如果智能体的 a[i].f 函数值超过了当前 fB 的最大值， 

• 则更新 fB 最大值。
• 将具有最佳值的智能体的索引存储在变量 ind 中。
• 根据智能体的 a[i].f 健壮度函数值更新智能体的尺寸大小 agent[i].size。
• 更新当前智能体的健壮度函数的最小值 fMin 和最大值 fMax。

3. 如果找到了具有最大健壮度值 f 的智能体，其坐标将通过 ArrayCopy 函数复制到数组 cB 中。

4. 更新智能体的能量和其他参数：

• 使用 CalculateEnergy 函数计算其能量。
• 计算摩擦力，并通过 fMin 和 fMax 进行归一化。
• 智能体的能量减少 energyLoss。
• 如果新的能量值大于当前的能量值，那么能量会增加损失值的一半，并且智能体的饥饿度会被重置。否则，饥饿度会增加。
• 根据智能体的当前大小和饱腹感计算生长因子，并更新智能体的尺寸大小。

5. 调用过程：在函数的末尾，会调用 EvolutionProcess 和 AdaptationProcess 方法。这些方法负责根据智能体的当前状态进一步实现其进化和适应性。

总的来说，Revision 函数负责根据智能体的特征和相互作用来更新种群中智能体的状态。它包括分析、更新以及调用额外的过程，这使得模拟种群动态成为可能。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;

      ind = i;
    }

    agent [i].size = a [i].f;

    if (a [i].f < fMin) fMin = a [i].f;
    if (a [i].f > fMax) fMax = a [i].f;
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    agent [i].energy   = CalculateEnergy (i);

    agent [i].friction = u.Scale (a [i].f, fMin, fMax, 0.1, 1.0, false);

    agent [i].energy -= energyLoss;

    double newEnergy = CalculateEnergy (i);

    if (newEnergy > agent [i].energy)
    {
      agent [i].energy += energyLoss / 2;
      agent [i].hunger = 0;
    }
    else
    {
      agent [i].hunger++;
    }

    double growthRate = maxGrowthRate * agent [i].size / (agent [i].size + halfSaturationConstant);

    agent [i].size *= (1 + growthRate);
  }

  //----------------------------------------------------------------------------
  EvolutionProcess  ();
  AdaptationProcess ();
}
//——————————————————————————————————————————————————————————————————————————————

让我们来描述一下 EvolutionProcess() 函数。它负责种群中智能体的进化。该函数的主要目的是找到健壮度最低的智能体（最低的藻类），并将其坐标替换为随机更健壮的智能体（更高的藻类）的坐标。

1. 寻找健壮度最低的智能体：

• 初始化变量 smallestIndex。它将存储健壮度最低的智能体的索引。设置初始值为 0。
• 循环遍历所有智能体（从第一个开始），并比较它们的健壮度。如果当前智能体的健壮度小于索引为 smallestIndex 的智能体的健壮度，则更新 smallestIndex。

2. 复制坐标：

• 初始化用于存储随机智能体索引的变量 m。
• 循环遍历从 0 到 coords 的所有坐标。
• 在循环内部，调用 u.RNDminusOne(popSize) 方法。它负责生成在 0 到 popSize - 1 之间的随机索引 m。
• 然后，将索引为 smallestIndex 的健壮度最低的智能体坐标替换为索引为 m 的随机智能体坐标。

EvolutionProcess 函数实现了一种简单的进化机制，其中种群中健壮度最低的智能体获得了随机智能体的坐标。这种操作是适应性机制的一部分，允许智能体通过从其他智能体中选择更成功的坐标来改善它们的特征。总体而言，它执行了算法的组合功能。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::EvolutionProcess ()
{
  int smallestIndex = 0;

  for (int i = 1; i < popSize; i++)
  {
    if (agent [i].size < agent [smallestIndex].size) smallestIndex = i;
  }

  int m = 0;

  for (int c = 0; c < coords; c++)
  {
    m = u.RNDminusOne (popSize);

    a [smallestIndex].c [c] = a [m].c [c];
  }
}
//——————————————————————————————————————————————————————————————————————————————

让我们更详细地看一下 AdaptationProcess() 函数的代码。它负责根据智能体的饥饿度和尺寸大小对种群中的智能体进行适应性调整。该函数的主要目标是在满足一定的适应概率条件时，改变最饥饿的智能体的坐标。

1. 寻找最饥饿的智能体（藻类）：

• 初始化存储最饥饿智能体索引的变量 starvingIndex。设置初始值为 0。
• 循环遍历所有智能体（从第一个开始），并比较饥饿度。如果当前智能体的饥饿度大于索引为 starvingIndex 的智能体的饥饿度，则更新 starvingIndex。

2. 检查适应性概率：

• 使用生成随机数（概率）的 u.RNDprobab() 方法。如果这个数字小于给定的适应性概率（adaptationProbability），则执行以下代码块。

3. 寻找最高的藻类 - 智能体：

• 类似于第一步，在这里寻找种群中最高的智能体的索引。最初，将 biggestIndex 设置为 0。
• 循环遍历所有智能体，如果当前智能体更高，则更新 BiggestIndex。

4. 适应性坐标：

• 循环遍历所有坐标。
• 通过加上计算得出的值来更新索引为 starvingIndex 智能体的坐标，该值是最高智能体和最饥饿智能体坐标之间的差值乘以随机概率。
• 然后使用 u.SeInDiSp() 方法对坐标进行归一化，该方法检查并调整坐标在指定的 rangeMin、rangeMax 和 rangeStep 范围内。

5. 更新智能体状态：

• 通过数组 a 中的健壮度值 f 更新智能体的尺寸大小。
• 将 hunger 水平设置为 0，这意味着智能体已经充满能量了。
• 将智能体的 energy 设置为 1.0。这是最大值。

AdaptationProcess 函数实现了适应性机制，允许最饥饿的智能体在满足概率条件时通过从最高的智能体那里借用坐标来改善自己的坐标。这是模拟一个自然选择系统的一部分，智能体通过适应环境来提高其生存机会。

//——————————————————————————————————————————————————————————————————————————————
void C_AO_AAA::AdaptationProcess ()
{
  int starvingIndex = 0;

  for (int i = 1; i < popSize; i++) if (agent [i].hunger > agent [starvingIndex].hunger) starvingIndex = i;
  
  if (u.RNDprobab () < adaptationProbability)
  {
    int biggestIndex = 0;

    for (int i = 1; i < popSize; i++) if (agent [i].size > agent [biggestIndex].size) biggestIndex = i;

    for (int j = 0; j < coords; j++)
    {
      a [starvingIndex].c [j] += (a [biggestIndex].c [j] - a [starvingIndex].c [j]) * u.RNDprobab ();

      a [starvingIndex].c [j] = u.SeInDiSp (a [starvingIndex].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }

    agent [starvingIndex].size   = a [starvingIndex].f;
    agent [starvingIndex].hunger = 0;
    agent [starvingIndex].energy = 1.0;
  }
}
//——————————————————————————————————————————————————————————————————————————————

接下来是 CalculateEnergy 函数的代码。该函数旨在根据智能体的特征（如菌落大小、能量水平和营养浓度）计算给定智能体的能量。该函数返回的能量值将被用于算法的其他部分。

1. 变量初始化：

• colony_size — 使用 index 获取藻类的高度。
• max_growth_rate — 最大生长速率。
• half_saturation_constant — 饱和常数的一半。

2. 健壮度函数归一化：计算营养浓度的归一化值。其计算规则为 f（来自数组 a）与最小值 fMin 之差与范围 fMax 和 fMin 之间的比率。加上 1e-10 可以防止除以0。

3. 获取当前生长速率：current_growth_rate — 获取智能体当前的能量值，也可解释为当前的生长速率。

4. 计算生长速率：growth_rate — 由最大生长速率、归一化的营养浓度和当前生长速率计算得出。该方程考虑了饱和效应，即随着当前生长速率的增加，整体生长速率反而降低。

5. 能量计算：计算 growth_rate 与某些能量损失（energyLoss）之间的差值得到 energy 。该值表示智能体在考虑损失后获得的能量。

6. 如果计算出的能量为负值，则将其设置为 0。这样可以防止出现负的能量值。

7. 函数返回计算出的能量值。

CalculateEnergy 函数模拟了一个过程，在该过程中，智能体根据其生长速率、菌落大小和营养浓度获得能量。它还考虑了能量损失，以确保智能体在模拟中的行为符合现实。 

//——————————————————————————————————————————————————————————————————————————————
double C_AO_AAA::CalculateEnergy (int index)
{
  double colony_size              = agent [index].size;
  double max_growth_rate          = maxGrowthRate;
  double half_saturation_constant = halfSaturationConstant;

  // Use the normalized value of the fitness function
  double nutrient_concentration = (a [index].f - fMin) / (fMax - fMin + 1e-10);

  double current_growth_rate = agent [index].energy;

  double growth_rate = max_growth_rate * nutrient_concentration / (half_saturation_constant + current_growth_rate) * colony_size;

  double energy = growth_rate - energyLoss;

  if (energy < 0) energy = 0;

  return energy;
}
//——————————————————————————————————————————————————————————————————————————————

最后的方法是实现竞争式选择机制。TournamentSelection 方法根据其健壮度函数值从种群中选择两个候选者中的一个。它返回具有最佳健壮度值的候选者索引。竞争式选择提供了选择方式。我们已经在上面讨论了在种群中智能体之间的概率分布。

//——————————————————————————————————————————————————————————————————————————————
int C_AO_AAA::TournamentSelection ()
{
  int candidate1 = u.RNDminusOne (popSize);
  int candidate2 = u.RNDminusOne (popSize);

  return (a [candidate1].f > a [candidate2].f) ? candidate1 : candidate2;
}
//——————————————————————————————————————————————————————————————————————————————

测试结果

AAA测试台结果：

打印输出和对算法运行的可视化都显示出收敛性较弱，测试结果也证实了这一点。遗憾的是，我对理想结果的预期并没有实现。考虑到算法的复杂搜索策略，很难确定其效率低下的原因，因为它对全局最优的定位能力较弱。然而，尽管存在这些缺点，该算法仍然有其优势。

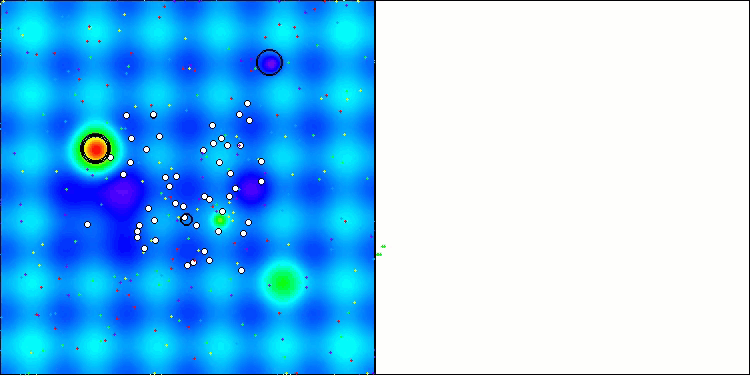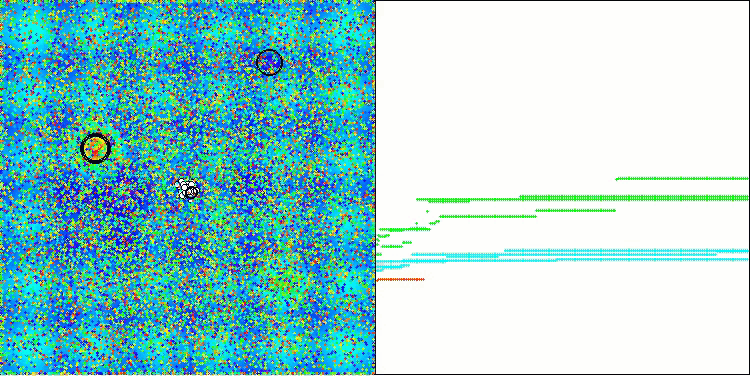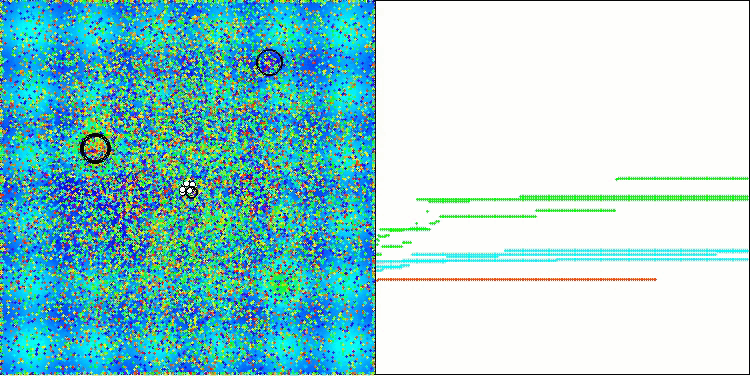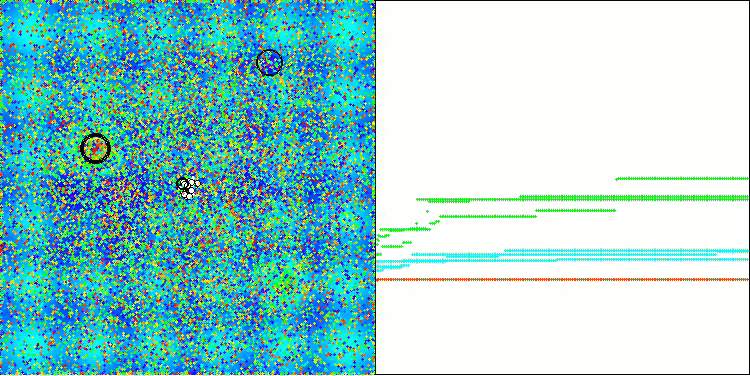
AAA在 Hilly 测试函数上

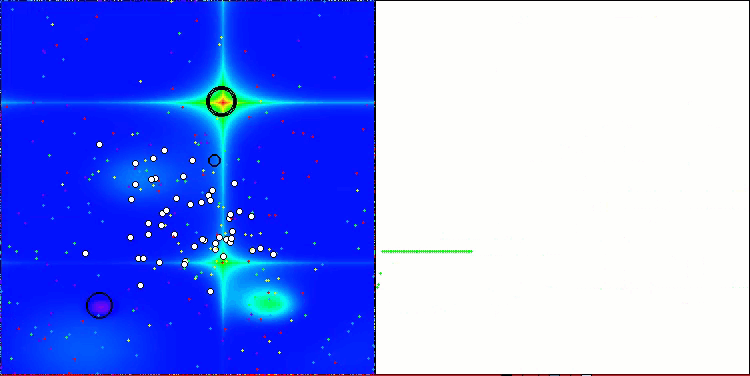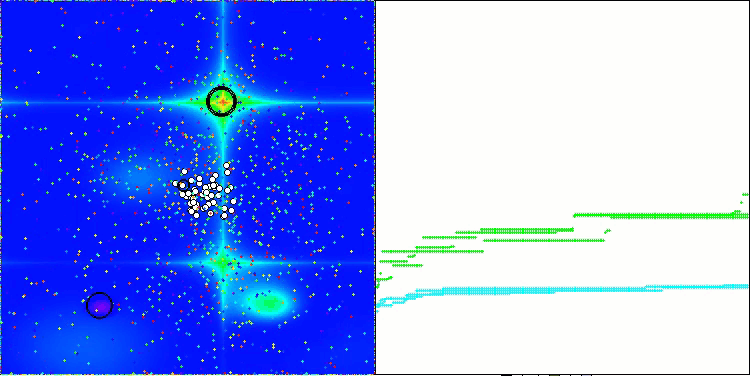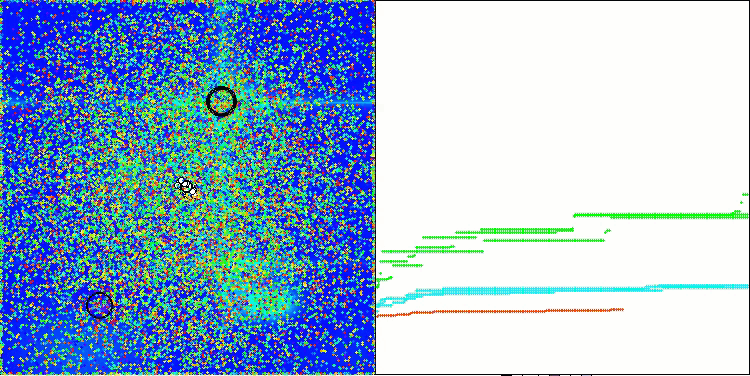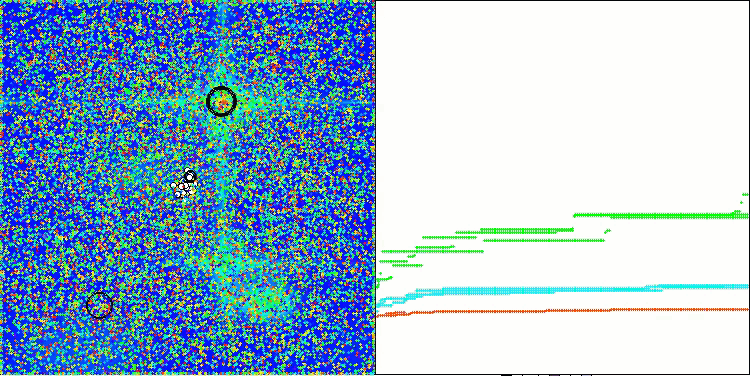
AAA在 Forest 测试函数上

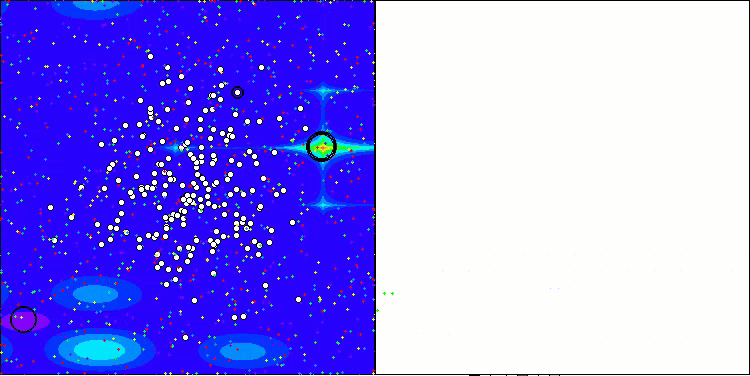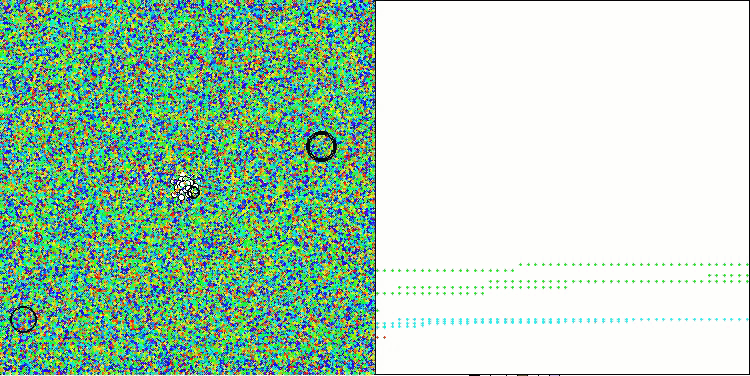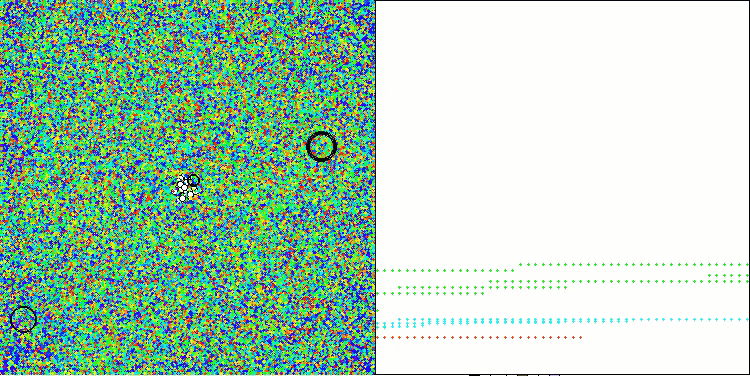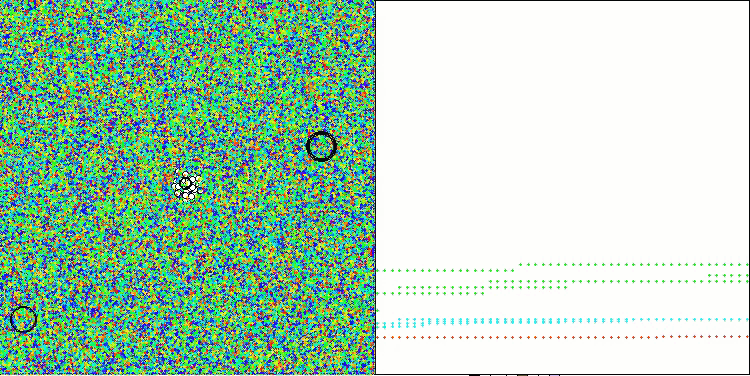
AAA在 Megacity 测试函数上

根据测试结果，该算法在评分表中排名第36位。

#	AO	说明	Hilly值			Hilly最终值	Forest值			Forest最终值	Megacity (离散)			Megacity最终值	最终结果	最大百分比
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	ANS	跨邻域搜索	0.94948	0.84776	0.43857	2.23581	1.00000	0.92334	0.39988	2.32323	0.70923	0.63477	0.23091	1.57491	6.134	68.15
2	CLA	密码锁算法	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	AMOm	动物迁徙优化M	0.90358	0.84317	0.46284	2.20959	0.99001	0.92436	0.46598	2.38034	0.56769	0.59132	0.23773	1.39675	5.987	66.52
4	(P+O)ES	(P+O) 进化策略	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
5	CTA	彗星尾算法	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
6	SDSm	随机扩散搜索 M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
7	ESG	社会群体的进化	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
8	SIA	模拟各向同性退火	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
9	ACS	人工协同搜索	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
10	ASO	无序社会优化	0.84872	0.74646	0.31465	1.90983	0.96148	0.79150	0.23803	1.99101	0.57077	0.54062	0.16614	1.27752	5.178	57.54
11	TSEA	龟壳演化算法	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
12	DE	差分进化	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
13	CRO	化学反应优化	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
14	BSA	鸟群算法	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
15	HS	和声搜索	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
16	SSG	树苗播种和生长	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
17	(PO)ES	(PO) 进化策略	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
18	BSO	头脑风暴优化	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
19	WOAm	鲸鱼优化算法M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
20	AEFA	人工电场算法	0.87700	0.61753	0.25235	1.74688	0.92729	0.72698	0.18064	1.83490	0.66615	0.11631	0.09508	0.87754	4.459	49.55
21	ACOm	蚁群优化 M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
22	BFO-GA	细菌觅食优化 - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
23	ABHA	人工蜂巢算法	0.84131	0.54227	0.26304	1.64663	0.87858	0.47779	0.17181	1.52818	0.50923	0.33877	0.10397	0.95197	4.127	45.85
24	ASBO	适应性社会行为优化	0.76331	0.49253	0.32619	1.58202	0.79546	0.40035	0.26097	1.45677	0.26462	0.17169	0.18200	0.61831	3.657	40.63
25	MEC	思维进化计算	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
26	IWO	入侵杂草优化	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
27	Micro-AIS	微型人工免疫系统	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
28	COAm	布谷鸟优化算法 M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
29	SDOm	螺旋动力学优化 M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
30	NMm	Nelder-Mead方法 M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
31	FAm	萤火虫算法 M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
32	GSA	引力搜索算法	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
33	BFO	细菌觅食优化	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
34	ABC	人工蜂群	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
35	BA	蝙蝠算法	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
36	AAA	人工藻类算法	0.50007	0.32040	0.25525	1.07572	0.37021	0.22284	0.16785	0.76089	0.27846	0.14800	0.09755	0.52402	2.361	26.23
37	SA	模拟退火	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
38	IWDm	智能水滴 M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
39	PSO	粒子群优化	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
40	Boids算法	虚拟生物算法	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
41	MA	猴群算法	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
42	SFL	混合蛙跳算法	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
43	FSS	鱼群搜索	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
44	RND	随机	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
45	GWO	灰狼优化算法	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32

总结

打印输出显示收敛性较低。我对该算法的能力有些失望：尽管使用了多种方法和复杂的步骤逻辑，但最终它在表格中的排名非常靠后。也许，我们应该更多地关注并理解所使用的方法，因为数量并不总是能保证质量。读者可以自由地对其进行实验，如果算法显示出更好的结果，请分享出来。我期待关于文章的评论。

算法的积极方面包括在拥有1000个变量的森林（Forest ）函数和大都市（Megacity）函数上，与最接近的竞争对手相比，取得了较好的结果。这表明该算法在处理具有“尖锐”极值和离散问题的可扩展性方面具有潜力。

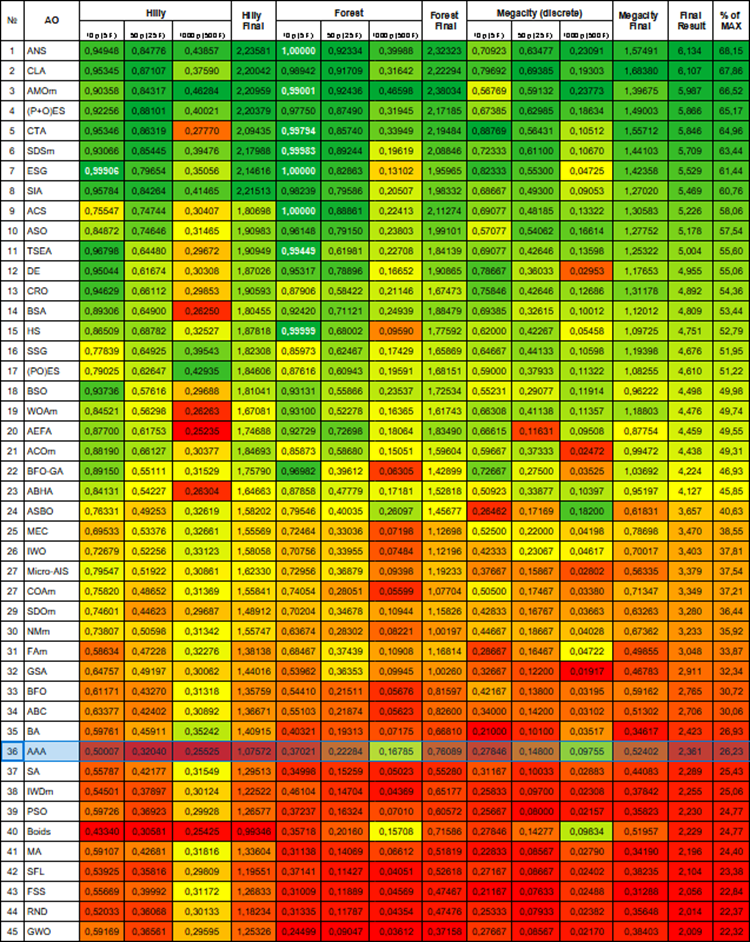
图1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

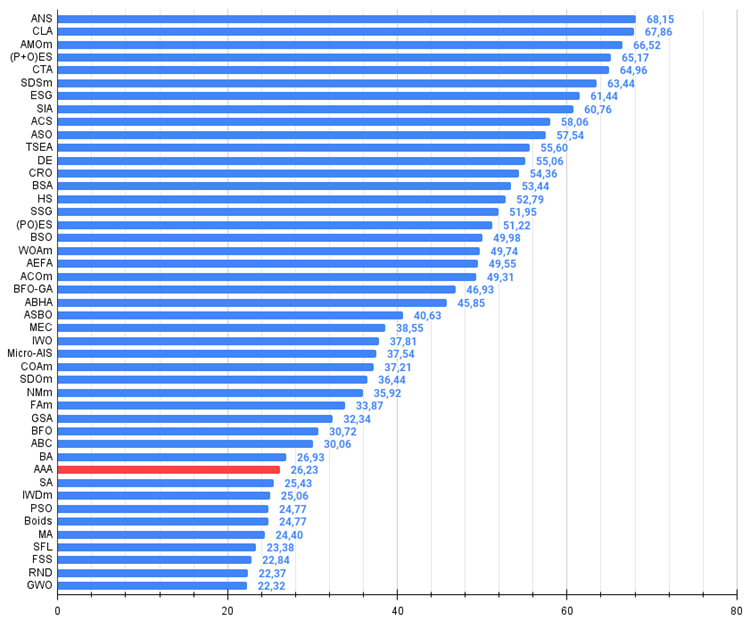
图例2. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）

AAA的优缺点：

优势：

1. 有前景的理念和创新的方法。

缺点：

1. 参数数量众多（配置非常困难）。
   
2. 收敛性较弱。
3. 难以调试。

文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• 代码库：https://www.mql5.com/ru/code/49355