
您应当知道的 MQL5 向导技术(第 36 部分):依据马尔可夫(Markov)链的 Q-学习
概述
由向导组装的智能系统的自定义信号类,能够承担各种值得探索的角色,我们继续寻求当 Q-学习算法与马尔可夫(Markov)链配对时,如何帮助改进多层感知器网络的学习过程。Q-学习是强化学习的若干种(大约 12 种)算法之一,故本质上,这也是对如何将该主题实现为自定义信号,并在由向导组装的智能系统中进行测试的考察。
故此,本文的结构将从强化学习作为源头,详述 Q-学习算法及其轮转阶段,研究如何将马尔可夫链集成到 Q-学习之中,然后一如既往地以策略测试报告终结。强化学习能当作独立的信号生成器,因为它的周期(“局次”)本质上是一种学习形式,即把结果量化为“参与者”所参与的每个“环境”的“奖励”。下面讲述引号中的这些术语。然而,我们并未将强化学习用作原生信号,而是凭借其能力,并补充多层感知器,来推进学习过程。
鉴于强化学习是机器学习训练中,除监督学习和无监督学习之外的第三大标准,我认为我们应让它更多地介入 MLP 的损失函数,因为在某种意义上它分别依据 “评论者奖励” 和 “环境状态” 来充当监督和无监督之间的行进选择。这两个加引号的术语会在下一章节里讲述;然而,这意味着大部分预测仍然取决于 MLP,强化学习更多地扮演着从属角色。此外,马尔可夫链的使用也是对强化学习的补充,因为从 “Q-映射” 中选择的 “参与者” 往往足以实现 Q-学习算法,不过我们将其包含在此,是为了解它所提供测试结果中的差异(如果有的话)之含义。
强化学习概览
强化学习,我们在上面讲述的是机器学习训练的第三条腿,是在训练过程中平衡探索和利用两者的一种方式。这要归功于其评估每轮训练的周期性方式,其中一轮训练称为局次。这个周期性表示如下图:
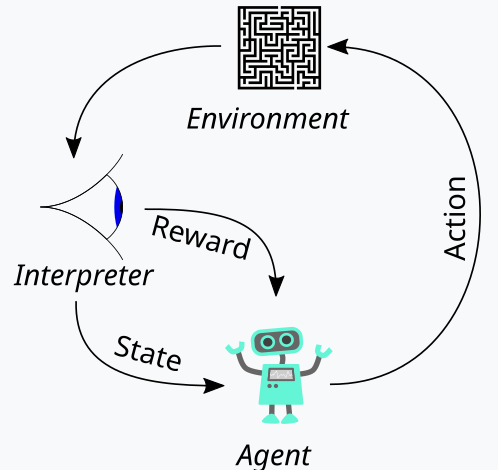
故据此,我们在强化学习过程中有一连串步骤。开端处,是一名“个体”,代表主方行权,在我们的例子中是 MLP,当面对更新的 Q-学习映射、或内核、或矩阵时,选择理想的行动方针。该映射是所有可能的环境状态记录,以及针对每个可用状态可能采取的动作的概率分布。
概括这一点的最佳途径,就是我们走一遍我们为本文选择的环境的实现。作为交易者,我们在考察市场定义时,往往不仅要依据它们的短期动作 ,还要依据它们的趋势、或长期特征。故此,如果我们专注于 3 个基本衡量度,即看涨、看跌、和横盘,那么这三个衡量度中的每一个都有较短时间帧、和较长时间帧。故此,本质上,我们的“环境”是一个包含 9 个指数的空间(短期与长期为 3 x 3),其中像 0 这样的指数表示短期和长期看跌,指数 4 表示短期和长期市场横盘整理,而指数 8 表示在两个时间横向范围内都看涨,等等。
环境选择要依靠与其名称相似的函数帮助,其源代码如下:
//+------------------------------------------------------------------+ // Indexing new Environment data to conform with states //+------------------------------------------------------------------+ void Cql::Environment(vector &E_Row, vector &E_Col, vector &E) { if(E_Row.Size() == E_Col.Size() && E_Col.Size() > 0) { E.Init(E_Row.Size()); E.Fill(0.0); for(int i = 0; i < int(E_Row.Size()); i++) { if(E_Row[i] > 0.0 && E_Col[i] > 0.0) { E[i] = 0.0; } else if(E_Row[i] > 0.0 && E_Col[i] == 0.0) { E[i] = 1.0; } else if(E_Row[i] > 0.0 && E_Col[i] < 0.0) { E[i] = 2.0; } else if(E_Row[i] == 0.0 && E_Col[i] > 0.0) { E[i] = 3.0; } else if(E_Row[i] == 0.0 && E_Col[i] == 0.0) { E[i] = 4.0; } else if(E_Row[i] == 0.0 && E_Col[i] < 0.0) { E[i] = 5.0; } else if(E_Row[i] < 0.0 && E_Col[i] > 0.0) { E[i] = 6.0; } else if(E_Row[i] < 0.0 && E_Col[i] == 0.0) { E[i] = 7.0; } else if(E_Row[i] < 0.0 && E_Col[i] < 0.0) { E[i] = 8.0; } } } }
该代码严格应用在我们的 9-指数环境,不能用在大小不同的环境矩阵。在定义该环境矩阵时,我们用到了一个称为 'scale' 的额外输入参数。这个伸缩度有助于将我们的长期框架横向范围与我们的短期框架窗口计算出比例或比率。默认值为 5,这意味着在环境矩阵的一个轴上,我们基于价格变化在另一个轴上“绘制”另一个周期内的价格变化,将状态标记为看涨、持平、或看跌。我说 '绘制' 是因为这两个轴只为当前状态提供坐标点。从 0 到 8 的指数只是将该矩阵扁平化为数组,但从随附的源代码中可以看出,对 'row' 和 'col' 的连续引用仅指向定义当前状态的环境矩阵中可能的 x 和 y 坐标读数。
Q-学习映射针对在任何这些环境状态中可能采取的动作添加权重来重现该环境状态数组。因为在我们的例子中,我们正在考察在每种状态下可以采取的 3 种可能的动作,即买入、卖出、或啥事都不做,Q-学习映射中的每个状态都有一个大小为 3 的数组,记录哪个动作最合适。分数值越高,越合适。上面周期图示中的另一个主要实体是观察者,我们将其称为“评论者”。评论者首先负责判定参与者动作的“奖励”。什么是奖励?嗯,这将取决于强化学习的用途,但就我们的目的而言,基于参与者可能的 3 个动作,我们使用价格变化的原生举牌数值盈利作为奖励。
故此,如果该价格变化是负的,而我们最后的行动是卖出,那么这个变化的量级权当是一种奖励。如果在之前的买入动作之后变化为正,亦同样适用。然而,若最后的动作是买入,且我们的价格变化为负值,那么这个负值的大小权当一种惩罚,如同卖出后的价格变化总是乘以负值,这意味着任何由此产生的负乘积都将作为我们在该特定状态(即我们的环境、或市场短期和长期价格行为的指数)所采取动作的惩罚。
尽管,这个奖励值需要归一化,这就是为什么我们调用 CriticRreward 函数将其保持在 0.0 到 1.0 的范围内。所有负值都在 0.0 到 0.5 之间,而正值则归一化为 0.5 到 1.0 之间。执行该操作的源代码如下所示:
//+------------------------------------------------------------------+ // Normalize reward via off-policy //+------------------------------------------------------------------+ double Cql::CriticReward(double MaxProfit, double MaxLoss, double Float) { double _reward = 0.0; if(MaxProfit >= Float && Float >= MaxLoss && MaxLoss < MaxProfit) { _reward = (Float - MaxLoss) / (MaxProfit - MaxLoss); } return(_reward); }
奖励值的更新总是发生在训练过程中期,而非在开始时进行一次。这意味着我们需要不断地将更新的 reward-max、reward-min 和 reward-float 参数值传递给反向传播函数,如此可将它们统合到进程之中。为成此愿,我们首先修改学习结构,其本用于存储在每次反向传播运行时可调用的学习变量。使用结构实际上令我们的代码易于修改,因为我们仅需将我们需要的额外新变量添加到结构中的现有变量列表当中即可。这显然不太容易出错,并且与必须修改函数输入参数列表里的结构变量形成鲜明对比。那样肯定很笨拙。修改后的学习结构现在如下所示:
//+------------------------------------------------------------------+ //| Learning Struct | //+------------------------------------------------------------------+ struct Slearning { Elearning type; int epochs; double rate; double initial_rate; double prior_rate; double min_rate; double decay_rate_a; double decay_rate_b; int decay_epoch_steps; double polynomial_power; double ql_reward_max; double ql_reward_min; double ql_reward_float; vector ql_e; Slearning() { type = LEARNING_FIXED; rate = 0.005; prior_rate = 0.1; epochs = 50; initial_rate = 0.1; min_rate = __EPSILON; decay_rate_a = 0.25; decay_rate_b = 0.75; decay_epoch_steps = 10; polynomial_power = 1.0; ql_reward_max = 0.0; ql_reward_min = 0.0; ql_reward_float = 0.0; ql_e.Init(1); ql_e.Fill(0.0); }; ~Slearning() {}; };
此外,在调用损失函数时,我们有必要对反向传播函数进行一些更改。这是因为我们现在为损失函数引入了一个新的、或从属的枚举,其清单如下:
//+------------------------------------------------------------------+ //| Custom Loss-Function Enumerator | //+------------------------------------------------------------------+ enum Eloss { LOSS_TYPICAL = -1, LOSS_SVR = 1, LOSS_QL = 2 };
其中一个枚举是 'LOSS_SVR' ,它配合支持向量回归来衡量损失,我们在上一篇文章中谈到过该方法。另外两个是 'LOSS_TYPICAL' 损失,当选择时默认为 MQL5 中的内置损失函数列表,另一个是 'LOSS_QL',其中 QL 代表 Q-学习,当它被选中时,含有 Q-学习的强化学习通过提供目标(或标签)向量来通知学习过程,其中 MLP 预测可进行比较。反向传播函数中的 If 子句会按如下方式进行检查:
//+------------------------------------------------------------------+ //| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON. | //+------------------------------------------------------------------+ //| | //| -Extra Validation check of MLP architecture settings is performed| //| at run-time. | //| Chcecking of 'validation' parameter should ideally be performed | //| at class instance initialisation. | //| | //| -Run-time Validation of learning rate, decay rates and epoch | //| index is performed as these are optimisable inputs. | //+------------------------------------------------------------------+ void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1) { ... if(THIS.loss_custom == LOSS_SVR) { _last_loss = SVR_Loss(); } else if(THIS.loss_custom == LOSS_QL) { double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float); if(QL.act == 0) { _reward *= -1.0; } else if(QL.act == 1) { _reward = -1.0 * fabs(_reward); } QL.CriticState(_reward, Learning.ql_e); _last_loss = output.LossGradient(QL.Q_Loss(), THIS.loss_typical); } ... }
添加该自定义损失函数并未否定基于 MQL5 中内置枚举所用的旧损失函数的需求。我们只简单地将其重命名为 'typical_loss',并且如果输入 'custom_loss' 是 'LOSS_TYPICAL',则必须提供该值。
奖励值归一化后,会在 CriticState 函数中用来更新 Q-学习映射。Q 值的更新由以下公式控制:
其中:
- Q(s,a):在状态 s 时采取动作 a 的 Q-值。这表示该“状态-动作”对的预期未来奖励。
- α:学习率,介于 0 和 1 之间的数值,控制有多少新信息覆盖旧信息。较小的 α 意味着个体的学习速度较慢,而较大的 α 令其对最近的经验响应更快。
- r:在状态 s 时采取动作 a 后得到的最新奖励。
- γ:折扣系数,介于 0 和 1 之间的值,针对未来奖励进行折扣。较高的 γ 令个体更重视长期奖励,而较低的 γ 令其更专注于即时奖励。
- max a′ Q(s′,a′):涵盖所有可能动作 a′的下一个状态 s′的最大 Q-值,这表示从下一个状态 s′开始,个体对于可能的最佳未来奖励的评估
Q-学习映射的实际更新可以在 MQL5 中实现,如下所示:
//+------------------------------------------------------------------+ // Update Q-value using off-policy (Q-learning formula) //+------------------------------------------------------------------+ void Cql::CriticState(double Reward, vector &E) { int _e_row_new = 0, _e_col_new = 0; SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new); e_row[1] = e_row[0]; e_col[1] = e_col[0]; e_row[0] = _e_row_new; e_col[0] = _e_col_new; int _new_best_q = Action(); double _weighting = Q[e_row[0]][e_col[0]][_new_best_q]; if(THIS.use_markov) { LetMarkov(e_row[1], e_col[1], E); int _old_index = GetMarkov(e_row[1], e_col[1]); int _new_index = GetMarkov(e_row[0], e_col[0]); _weighting *= markov[_old_index][_new_index]; } Q[e_row[1]][e_col[1]][act] += THIS.alpha * (Reward + (THIS.gamma * _weighting) - Q[e_row[1]][e_col[1]][act]); }
在更新映射时,正更新的停用政策规则,其中下一个状态的最佳动作会用在更新旧动作。这与启用的政策动作形成对比,其中当前动作会在下一个状态中所用,来执行相同的更新。这是因为对于由环境矩阵中的行坐标和列坐标定义的任何状态,这是个体可执行的可能动作的标准数组。至于 Q-学习所用的停用政策更新,会选择最佳加权动作,不过对于启用政策更新的算法,在执行更新时会保留当前动作。最佳动作的选择是通过 'Action' 函数执行的,其代码如下:
//+------------------------------------------------------------------+ // Choose an action using epsilon-greedy //+------------------------------------------------------------------+ int Cql::Action() { int _best_act = 0; if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon) { // Explore: Choose random action _best_act = (rand() % THIS.actions); } else { // Exploit: Choose best action double _best_value = Q[e_row[0]][e_col[0]][0]; for (int i = 1; i < THIS.actions; i++) { if (Q[e_row[0]][e_col[0]][i] > _best_value) { _best_value = Q[e_row[0]][e_col[0]][i]; _best_act = i; } } } //update last action act = _best_act; return(_best_act); }
强化学习有点像监督学习,在于有一个奖励量值用于调整和优调在每个环境状态下的动作权重。另一方面,也同无监督学习那样使用环境矩阵,其坐标值(行索引和列索引的两个值)当作 MLP 的输入来用。因此,MLP 充当一个分类器,当以环境状态坐标作为输入时,它试图检测三个适用动作的正确概率分布。然后,如任何分类器 MLP 一样进行训练,但这次我们旨在把 MLP 的预测概率分布、与 Q-学习内核中作为 MLP 输入提供的 Q-学习映射坐标的概率分布之间的差异最小化。
马尔可夫转换的作用
马尔可夫链是概率随机模型,当投喂这些状态的时间序列时,它用转换矩阵来映射从一种状态移动到另一种状态的概率。这些概率模型本质上是无记忆的,因为转换到下一个状态的概率完全基于当前状态,而非基于之前状态的历史记录。这些转换可用于附加重要的环境矩阵中定义的各种状态。
现在,从我们在自定义信号中的用例来看,环境矩阵仅考虑了短期和长期框架的看涨、看跌、和横盘三种市场状态,令其成为一个 3 x 3 矩阵,故其暗示九种可能的状态。因为我们有九种可能的状态,这意味着我们的马尔可夫转换矩阵将是一个 9 x 9 矩阵,以便把一个环境状态的转换映射到另一个。因此,这必须能够将环境矩阵中的索引对转换为可在马尔可夫转换矩阵中使用的单一指数。实际上,我们最终需要两个函数,一个将环境行和列索引对转换为马尔可夫矩阵的单一指数,另一个在呈现马尔可夫转换矩阵指数时重建环境矩阵的行和列索引。这两个函数分别命名为 GetMarkov 和 SetMarkov,它们的源代码如下:
//+------------------------------------------------------------------+ // Getting markov index from environment row & col //+------------------------------------------------------------------+ int Cql::GetMarkov(int Row, int Col) { return(Row + (THIS.environments * Col)); }
以及:
//+------------------------------------------------------------------+ // Getting environment row & col from markov index //+------------------------------------------------------------------+ void Cql::SetMarkov(int Index, int &Row, int &Col) { Col = int(floor(Index / THIS.environments)); Row = int(fmod(Index, THIS.environments)); }
在开始执行马尔可夫计算时,我们需要获取两个环境状态坐标的马尔可夫等效索引,因为我们将转换该状态。一旦我们得到该索引,我们就可以提取在转换矩阵中沿此列转换到其它状态的概率,因为它们中的每一个都用作权重。正如预期,它们加起来都是 1,并且由于参与者已经从 Q-映射中选择了下一个状态,因此我们将其概率用作 1 分母的分子,这意味着在学习过程中,只有其概率被用作权重来增加 Q-映射中的新值。实现这一点的源代码已在上面的评论者状态函数中分享。
该学习过程本质上是按照其在马尔可夫转换矩阵中的概率成比例地对学习增量进行折扣。
此外,每当注册新柱线,且价格的时间序列得到更新时,我们都会执行转换矩阵计算。执行这些计算的代码如下:
//+------------------------------------------------------------------+ // Function to update markov matrix //+------------------------------------------------------------------+ void Cql::LetMarkov(int OldRow, int OldCol, vector &E) // { matrix _transitions; // Count the transitions _transitions.Init(markov.Rows(), markov.Cols()); _transitions.Fill(0.0); vector _states; // Count the occurrences of each state _states.Init(markov.Rows()); _states.Fill(0.0); // Count transitions from state i to state ii for (int i = 0; i < int(E.Size()) - 1; i++) { int _old_state = int(E[i]); int _new_state = int(E[i + 1]); _transitions[_old_state][_new_state]++; _states[_old_state]++; } // Reset prior values to zero. markov.Fill(0.0); // Compute probabilities by normalizing transition counts for (int i = 0; i < int(markov.Rows()); i++) { for (int ii = 0; ii < int(markov.Cols()); ii++) { if (_states[i] > 0) { markov[i][ii] = double(_transitions[i][ii] / _states[i]); } else { markov[i][ii] = 0.0; // No transitions from this state } } } }
作为一个无记忆的转换矩阵,我们上面的代码总是以新声明的矩阵开头,并且保存概率的类变量也用零值填充,以清除任何先前的历史记录。计算转换的方式很简单,因为我们在第一个 for 循环中获得了每个状态序列的计数,接着我们又用另一个 for 循环将每次转换得到的累积计数除以所做转换的状态总数。
实现自定义信号类
如前所述,我们正在使用作为分类器的 MLP 来处理主要预测,强化学习仅作为损失函数,充当从属角色。强化学习也能被优化或训练,通过最大化评论者奖励来输出可用的交易信号,不过这不是我们在此所做的,取而代之,它的角色只是次要的,因为就像在监督学习和无监督中一样,它只被用来量化目标函数。
正如我们过去使用 MLP 的文章中一样,我们使用价格变化作为数据输入的来源。回想一下,本文使用的环境矩阵是一个 3 x 3 矩阵,当权衡短期和长期框架时,其当作市场可能状态的网格。短期和长期框架的每个轴都有从看涨到横盘、再到看跌的量值或读数,它们构成了 3 x 3 网格。与该矩阵类似的是 Q-学习矩阵或映射,它也具有这个 3 x 3 网格,并附加了一个可能动作的数组,对参与者开放,持续为这些动作针对每个状态的适用性进行评分。正是这个适用性数组当作 MLP 的标签或训练目标。
尽管,MLP 的输入不会如同我们最近关于 MLP 的文章中那样是原生价格变化,而是短期和长期时间帧内最近或当前价格变化的环境状态坐标。此处用 '时间帧' 纯粹是为了说明衡量价格变化的不同时间尺度或视野。我们没有两个单独的时间帧作为信号类的输入来指导这些变化的量值,而是有一个标记为 'm_scale' 的输入整数型参数,它是 '长期时间帧' 相对于短期时间帧的倍数。由于短期时间帧使用单根价格柱线的变化,则 '长期时间帧' 得到的变化读数覆盖相当于 "scale" 输入参数的周期。该处理在 GetOutput 函数中执行,如下所示:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalQLM::GetOutput(int &Output) { m_learning.rate = m_learning_rate; for(int i = m_epochs; i >= 1; i--) { MLP.LearningType(m_learning, i); for(int ii = m_train_set; ii >= 0; ii--) { vector _in, _in_row, _in_row_old, _in_col, _in_col_old; if ( _in_row.Init(m_scale) && _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) && _in_row.Size() == m_scale && _in_row_old.Init(m_scale) && _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, m_scale) && _in_row_old.Size() == m_scale && _in_col.Init(m_scale) && _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) && _in_col.Size() == m_scale && _in_col_old.Init(m_scale) && _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale + ii + 1, m_scale) && _in_col_old.Size() == m_scale ) { _in_row -= _in_row_old; _in_col -= _in_col_old; vector _in_e; _in_e.Init(m_scale); MLP.QL.Environment(_in_row, _in_col, _in_e); int _row = 0, _col = 0; MLP.QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col); _in.Init(__MLP_INPUTS); _in[0] = _row; _in[1] = _col; MLP.Set(_in); MLP.Forward(); if(ii > 0) { vector _target, _target_data; if ( _target_data.Init(2) && _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) && _target_data.Size() == 2 ) { _target.Init(__MLP_OUTPUTS); _target.Fill(0.0); double _type = _target_data[0] - _in_row[1]; int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1)); _target[_index] = 1.0; MLP.Get(_target); m_learning.ql_e = _in_e; m_learning.ql_reward_float = _in_row[m_scale - 1]; m_learning.ql_reward_max = _in_row.Max(); m_learning.ql_reward_min = _in_row.Min(); if(i == m_epochs && ii == m_train_set) { MLP.QL.Action(); } MLP.Backward(m_learning, i); } } Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2)); } } } }
故此,正如我们从上面的源代码中所见,我们需要 4 个向量来获取 MLP 输入的坐标读数。一旦确定了这些,借助环境函数,将两个价格变化转换为单个马尔可夫指数,以及 SetMarkov 函数从马尔可夫指数提取这两个坐标,我们将它们填充到 'in' 向量当中,其是我们的输入 。MLP 分类器有一个非常基本的架构 2-8-3,它代表 2 个输入、8 个大小的隐藏层、和 3 个输出,对应于向参与者开放的三种可能动作。MLP 的输出本质上是一个概率映射图,它给出了做空(在索引 0 下)、啥都不做(在索引 1 下)、和做多(在索引 2 下)的数值。
强化学习训练过程衡量这些输出与附加到每个环境状态的相似向量的距离。
策略测试器结果
故此,一如既往,我们依据真实即刻报价数据执行优化和测试运行,纯粹是为了演示经由 MQL5 向导组装的含有该信号类的智能系统如何能够执行其基本功能。有关在 MQL5 向导中使用所附代码的指南,可在此处和此处找到。这些文章中并未那些组装好的智能系统、或交易系统在真实账户里进行交易做好大量勤奋的准备工作,而是留给读者。我们依据 GBPJPY 货币 2023 年日线时间帧内执行测试运行。我们引入了马尔可夫链作为对 Q-学习映射值进行加权的替代方案,因此我们运行了两个测试,一个没有马尔可夫链权重,另一个有权重。结果如下:
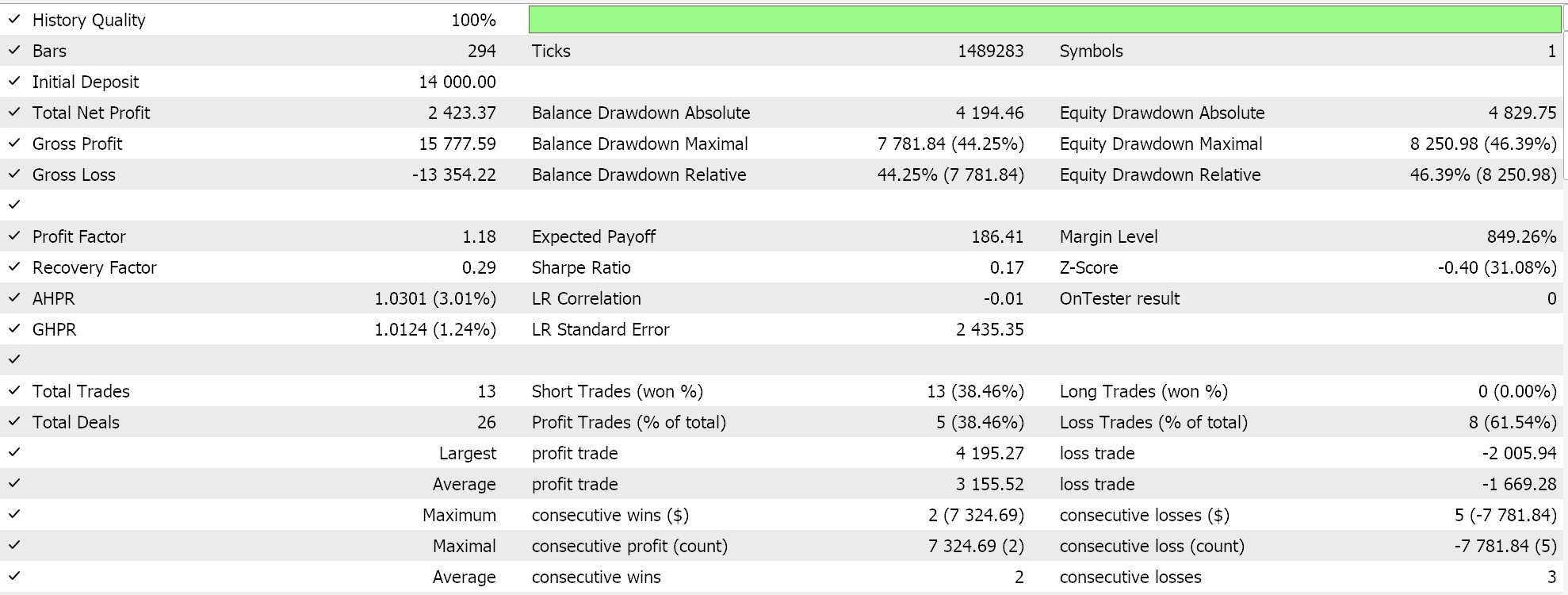
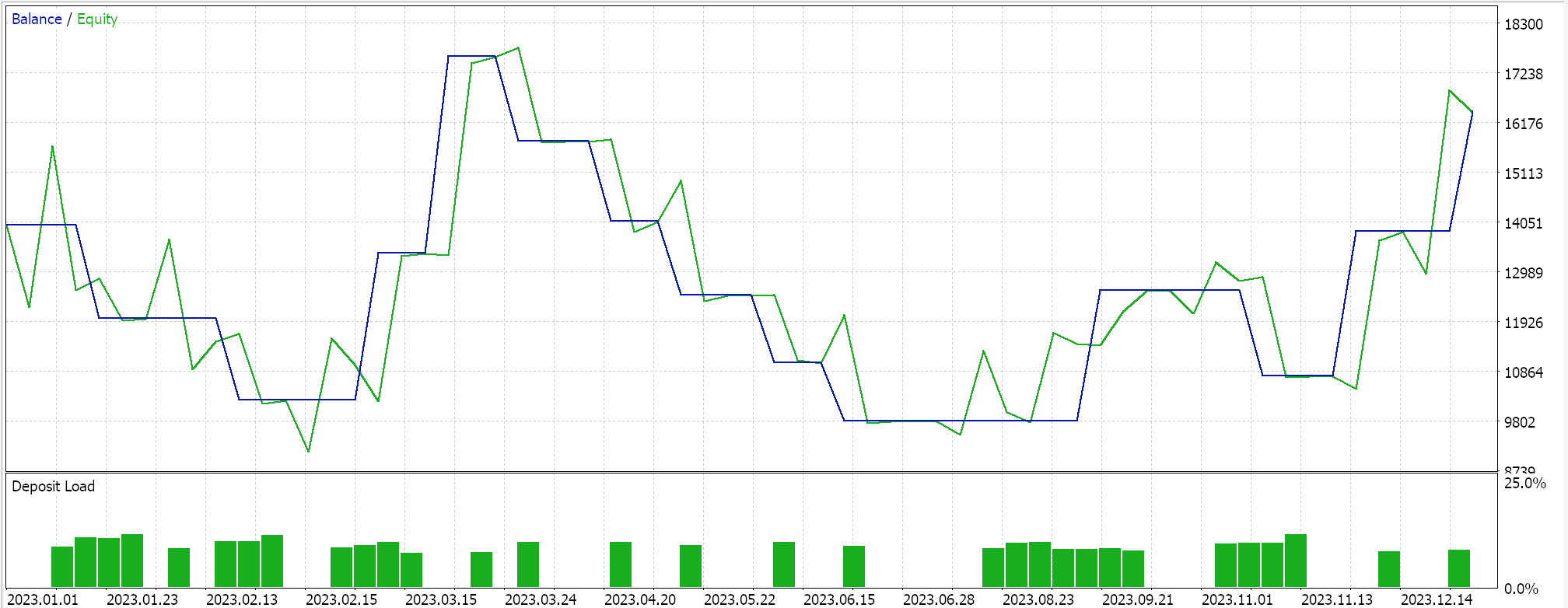
然后,没有马尔可夫加权的结果是:
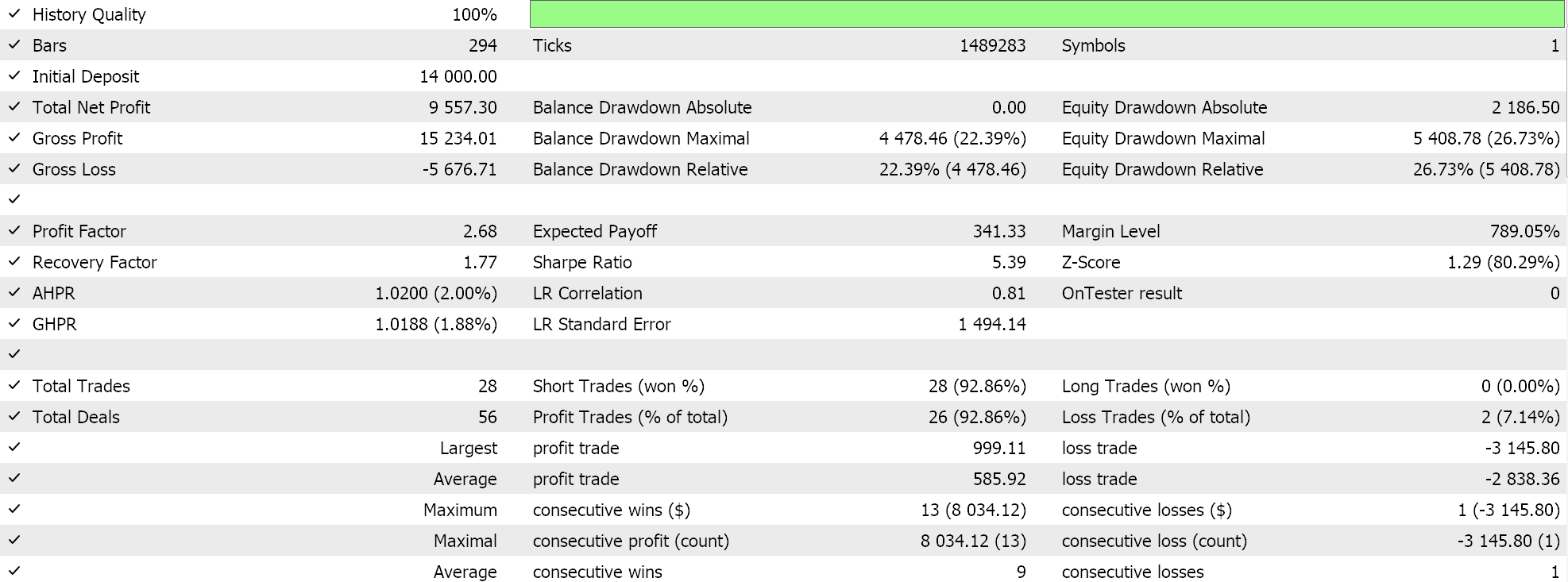
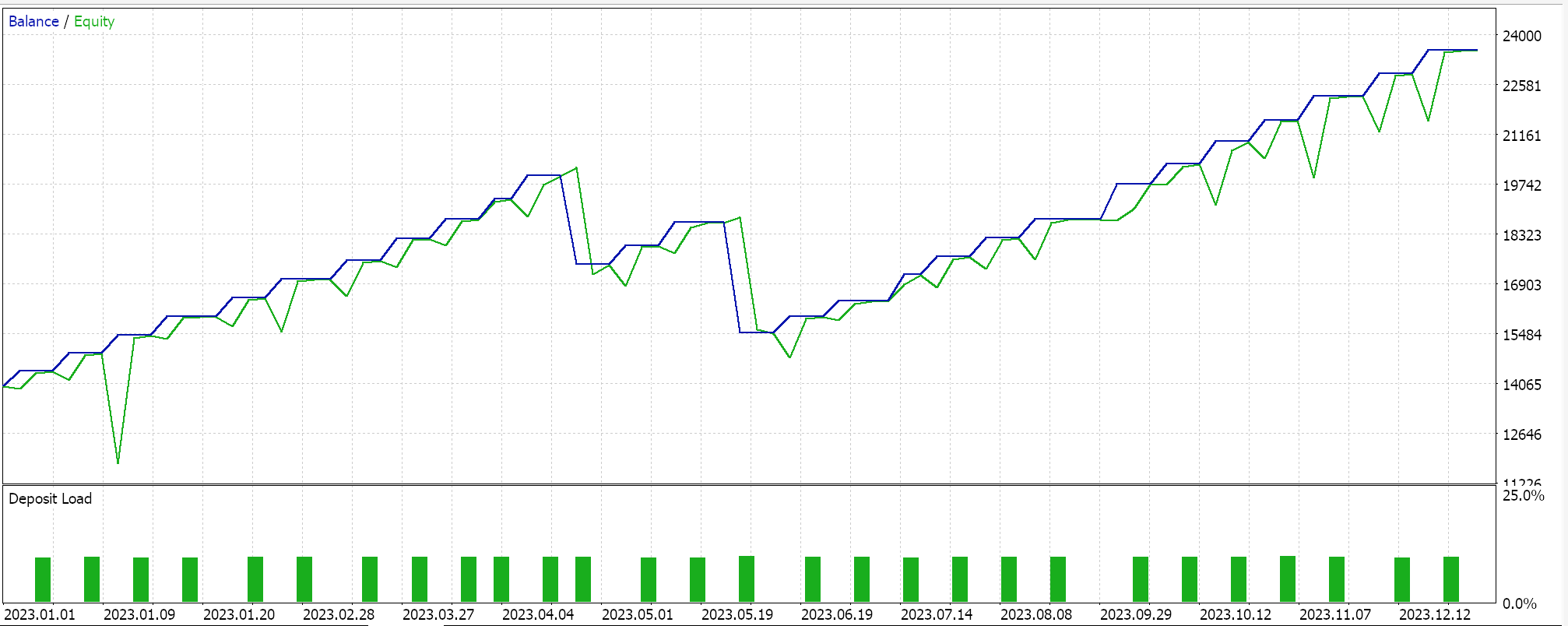
这些测试结果不是按照最佳优化设置实现的,也未采用这些设置执行前向测试的;因此,它们并不是对 Q-学习本身补充马尔可夫链的认可,尽管合理的论调和更综合的测试制度可为其造势。
结束语
在本文中,我们通过引入强化学习来强调 MQL5 向导的其它可能性,强化学习是除了已建立的监督学习和无监督学习方法之外,机器学习训练中的一种替代方案。我们试图在分类器 MLP 的训练中使用它,让它通知和指导训练过程,而不是将其作为原生信号生成器,这也是可能的。如此行事,在专注于 Q-学习算法的同时,我们探索了马尔可夫链,这是一个转换概率矩阵,可以作为强化学习训练过程的权重,并且我们在 2 个场景中展示了智能系统的测试运行;在没有马尔可夫链的情况下训练时,以及采用它们进行训练时。
我认为,与我之前的文章相比,这要复杂一些,因为我们将 2 个类引入我们的自定义信号,并且许多敏感的输入参数都取它们的默认值,未经任何重大调整,并需要为不熟悉该主题的人引入大量新术语。然而,这是我们处理这个广泛而深入的强化学习主题的开始,故我希望在以后的文章中,当我们重新审视这个主题时,它不会那么令人生畏。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15743
 创建 MQL5-Telegram 集成 EA 交易(第 4 部分):模块化代码函数以增强可重用性
创建 MQL5-Telegram 集成 EA 交易(第 4 部分):模块化代码函数以增强可重用性
 大气云模型优化(ACMO):实战
大气云模型优化(ACMO):实战
 美元和欧元指数图表 — MetaTrader 5 服务示例
美元和欧元指数图表 — MetaTrader 5 服务示例
