
Algoritmo de evolución del caparazón de tortuga (Turtle Shell Evolution Algorithm, TSEA)
Contenido:
1.Introducción
2.Aplicación del algoritmo
3.Resultados de las pruebas
1. Introducción
La tortuga es una de las creaciones más antiguas y sorprendentes de la naturaleza. Lleva un caparazón, símbolo de resistencia, protección y supervivencia. Este majestuoso escudo, formado durante su viaje vital, encarna no solo su protección física, sino que también simboliza su continuo desarrollo y la superación de obstáculos.
El dibujo de la concha supone un testimonio de la singularidad de su trayectoria evolutiva, que simboliza la armonía entre el tiempo y la propia criatura. El crecimiento del caparazón de las tortugas procede de un punto central llamado cordón umbilical. Desde allí se añaden nuevas capas de material al caparazón existente, lo que da lugar a la formación de diferentes patrones. Cada segmento del patrón representa un año o estación diferente del crecimiento de la tortuga. Capa tras capa, año tras año, el caparazón crece y madura con la tortuga, adoptando nuevos patrones, formando agrupaciones únicas que son un reflejo de sus experiencias vitales y de su crecimiento.
El caparazón de la tortuga consta de dos partes principales: la superior, llamada caparazón, y la inferior, llamada plastrón. El crecimiento del caparazón de las tortugas se produce mediante un proceso llamado metamorfosis. Los patrones del caparazón de las tortugas son resultado de una compleja interacción de muchos factores, como la genética, el entorno y el proceso de crecimiento del propio caparazón.
El caparazón de las tortugas está compuesto de tejido biológico y sustancias carbonatadas como el calcio y el magnesio. La estructura carbonatada del caparazón ofrece resistencia y protege los órganos internos de la tortuga. En las tortugas jóvenes, el caparazón está formado por placas de cartílago blando que con el tiempo se calcifican y se transforman en hueso duro. El caparazón crece gracias al depósito regular de nuevas capas de tejido óseo bajo la piel de la tortuga. Este proceso permite que el caparazón aumente de tamaño a medida que la tortuga crece y, con el paso del tiempo, puede dar lugar a nuevos patrones o cambios en los ya existentes.
Los dibujos del caparazón de la tortuga no son accidentales: se forman según determinados procesos biológicos y pueden clasificarse en diferentes grupos o "clústeres" en función de su forma, color y disposición. Por ejemplo, algunas tortugas tienen dibujos en forma de estrella, mientras que otras tienen dibujos semejantes a la piel del leopardo. Conforme crece el caparazón de la tortuga, sus dibujos pueden cambiar y evolucionar. Esto puede dar lugar a un cambio en el clúster al que pertenece el patrón. Por ejemplo, un patrón clasificado inicialmente como "patrón de estrella" puede volverse más complejo con el tiempo.
Debemos considerar además que los patrones del caparazón de cada tortuga son únicos, lo cual le ayuda a adaptarse a su entorno y a cumplir funciones importantes, como camuflarse o atraer a sus parejas reproductoras.
Los patrones del caparazón de tortuga me han inspirado para crear un algoritmo de optimización original, y la evolución del caparazón de tortuga se ha convertido en una metáfora del proceso de fusión y clusterización de datos, definiendo la creación de una nueva herramienta capaz de adaptarse y evolucionar en función de la experiencia y el conocimiento.
2. Aplicación del algoritmo
La idea del algoritmo de evolución del caparazón de tortuga consiste en emular el crecimiento del caparazón mediante la formación gradual de nuevas sectores de piel queratinizada que representan las soluciones a un problema de optimización. En este modelo, las mejores soluciones se volverán más duras y se encontrarán más cerca de la superficie exterior del caparazón, mientras que las soluciones menos exitosas permanecerán blandas y se situarán en el interior del caparazón.
En este contexto, el caparazón se divide en grupos que formarán un patrón en su superficie, mientras que sus capas se modelarán mediante una subdivisión vertical en grupos. El proceso de emulación del crecimiento del caparazón en el algoritmo implicará tanto el movimiento hacia arriba (hacia fuera) como hacia abajo (hacia dentro), así como la anchura. Una característica única de este algoritmo de optimización es la preservación de las soluciones menos exitosas, que se manifiesta en el crecimiento hacia el interior del caparazón. La capa interior del caparazón es la única que se expandirá en ambas direcciones, mientras que las demás capas solo lo harán hacia el exterior, sustituyendo las peores soluciones por otras nuevas. Cada clúster (capa) vertical tiene una capacidad limitada de soluciones; en caso de que no se alcance el número máximo, se realizará una simple adición de soluciones; de lo contrario, la solución se sustituirá según el principio descrito.
La figura 1 representa la clusterización de soluciones según su calidad y la distancia entre ellas. Para una mejor comprensión, utilizamos un ejemplo hipotético con un espacio de soluciones unidimensional. Este esquema permite visualizar cómo se forman los clústeres según la calidad y la proximidad de las soluciones entre sí.
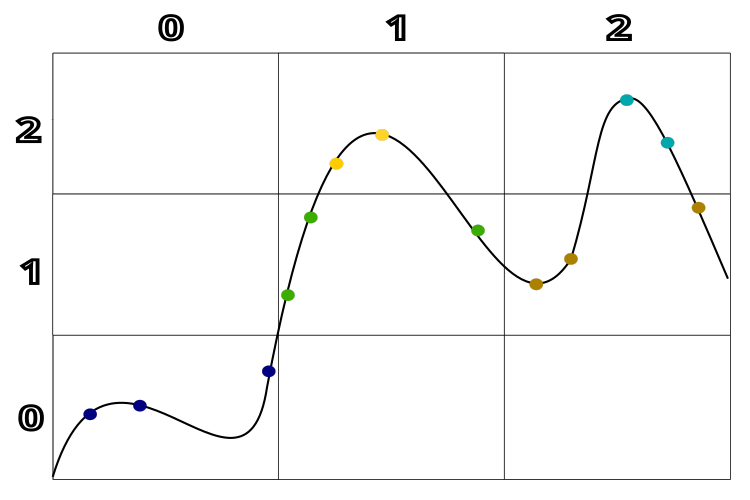
Figura 1. Clusterización según la calidad de las soluciones y según la distancia entre las mismas en el algoritmo TSEA.
Vamos a escribir el pseudocódigo del algoritmo TSEA:
1. Generamos individuos aleatorios en una población.
2. Calculamos la FF.
3. Realizamos la clusterización inicial de la población verticalmente.
4. Realizamos la clusterización inicial de la población K-Means horizontalmente.
5. Colocamos la población en un caparazón.
6. Generamos una nueva población a partir de los datos del caparazón:
6.1. Con una probabilidad de 0,8:
Seleccionamos un clúster verticalmente.
Seleccionamos con una probabilidad 0,5 el mejor agente de la celda, o cualquier agente aleatorio de la celda.
Con una probabilidad 0,6 para cada coordenada, utilizamos el agente seleccionado en la celda, o utilizamos la mejor solución global.
Luego utilizamos una distribución escalonada para crear una nueva coordenada para el agente.
6.2 O bien:
Seleccionamos un clúster verticalmente.
Elegimos dos clústeres verticalmente de los que seleccionar al azar un agente de cada uno.
Creamos una nueva coordenada como la media de las coordenadas de los agentes seleccionados.
7. Calculamos la FF.
8. Realizamos la clusterización vertical de la población.
9. Determinamos si los agentes pertenecen a clústeres de caparazones K-NN (método de los N vecinos más próximos).
10. Realizamos la clusterización vertical del caparazón cada 50 épocas.
11. Colocamos la población en un caparazón.
12. Repetimos desde el paso 6.
Seleccionamos el clúster verticalmente según la ley cuadrática (Fig. 2), que determinará la mayor probabilidad de un clúster de ser elegido en último (mejor) lugar de la lista, en comparación con el 0º (peor).
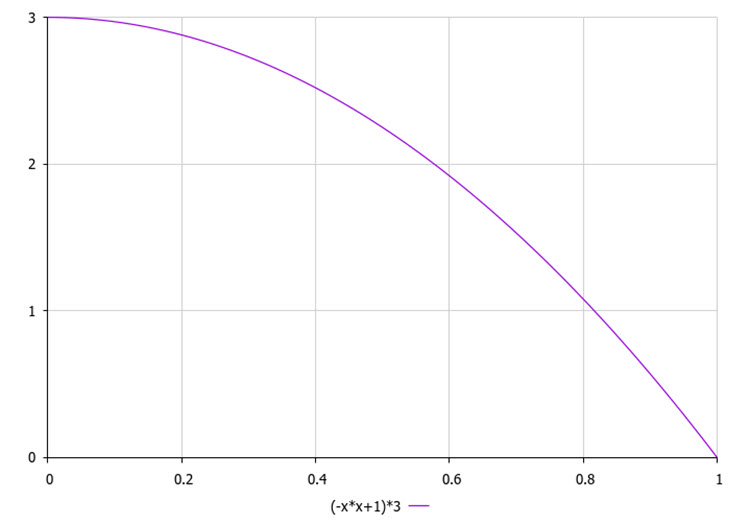
Figura 2. Ley de probabilidad de selección de clústeres en vertical (según la calidad), donde 3 será el número de clústeres.
Así pues, la lógica de creación de nuevos sectores del caparazón (agentes - soluciones al problema de optimización) será la siguiente:
- Selección de una capa del caparazón (clúster vertical). La probabilidad de seleccionar la capa superior, más dura, será mayor que la de seleccionar las capas inferiores, menos duras.
- Selección de sectores del caparazón a partir de clústeres horizontales en la capa seleccionada.
- "Empalme" de los sectores seleccionados.
La probabilidad de "empalme" (curado) será mayor en las capas superiores que en las inferiores.
Ahora que tenemos el pseudocódigo y la ley de selección de agentes en la población padre, podemos decir que la tarea está completada en un 99%. Obviamente, estoy bromeando, todavía tenemos que escribir el código.
El agente de optimización del algoritmo TSEA lo describiremos como una estructura "S_TSEA_Agent"; necesitaremos etiquetas de clúster verticales y horizontales.
1. La estructura contendrá los siguientes campos:
- c[] - array para almacenar las coordenadas del agente
- f - variable para almacenar la puntuación del agente (aptitud)
- label - etiqueta de pertenencia al clúster
- labelClustV - clusterización vertical
- minDist - distancia mínima al centroide más próximo
2. Init - método de la estructura "S_TSEA_Agent" que inicializará los campos de la estructura. Toma un argumento "coords" entero que se utilizará para redimensionar el array c usando la función ArrayResize.
3. f = -DBL_MAX - establece el valor inicial de la variable f igual al valor mínimo posible de un número de tipo double.
4. label = -1 y labelClustV = -1 - inicializa las etiquetas de pertenencia a clústeres con un valor de -1.
5. minDist = DBL_MAX - establece el valor inicial de la variable "minDist" igual al valor máximo posible del número de tipo duoble.
Este código representa la estructura básica de datos para los agentes en el algoritmo de optimización TSEA e inicializa sus campos cuando se crea un nuevo agente. Esto permite a los agentes almacenar información sobre su estado actual y actualizarla a medida que se ejecuta el algoritmo.
//—————————————————————————————————————————————————————————————————————————————— struct S_TSEA_Agent { double c []; //coordinates double f; //fitness int label; //cluster membership label int labelClustV; //clusters vertically double minDist; //minimum distance to the nearest centroid void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; label = -1; labelClustV = -1; minDist = DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Deberemos describir un caparazón de tortuga, que no es sino un array bidimensional con clústeres en vertical según adaptabilidad y clústeres en horizontal según la ubicación. Cada celda del array bidimensional contiene desde 0 hasta el valor máximo especificado en los parámetros externos del algoritmo.
El clúster horizontal lo describiremos usando la estructura "S_TSEA_horizontal", que contiene los campos:
- indBest - índice del mejor agente de la celda
- agent[] - array de estructuras S_TSEA_Agent, que se utiliza para almacenar los agentes
El clúster vertical puede describirse usando la estructura "S_TSEA_horizontal" que contiene los campos:
- cell[] - array de estructuras "S_TSEA_horizontal".
Así, el código nos ofrecerá una forma de describir el caparazón de la tortuga en dos direcciones de un array bidimensional, en cada celda del cual podremos almacenar los agentes de optimización. En esencia, un caparazón es una población padre especialmente estructurada a la que se accederá cómodamente cuando se creen los agentes hijo.
//—————————————————————————————————————————————————————————————————————————————— struct S_TSEA_horizontal { int indBest; S_TSEA_Agent agent []; }; struct S_TSEA_vertical { S_TSEA_horizontal cell []; }; //——————————————————————————————————————————————————————————————————————————————
Para realizar la clusterización, según el pseudocódigo dado, se utilizarán dos métodos de clusterización en el algoritmo TSEA: K-Means y K-NN. Ya hablamos de K-Means en el artículo sobre el algoritmo BSO, así que aquí nos limitaremos a recordar el aspecto de la estructura de los clústeres:
- centroid[] - array para almacenar las coordenadas del centroide de la celda
- f - variable para almacenar la puntuación del centroide (aptitud)
- count - número de agentes en el clúster
- agentList[] - lista de agentes en el clúster
- Init - método de la estructura "S_Cluster", que inicializa los campos de la estructura
//—————————————————————————————————————————————————————————————————————————————— struct S_Cluster { double centroid []; //cluster centroid double f; //centroid fitness int count; //number of points in the cluster void Init (int coords) { ArrayResize (centroid, coords); f = -DBL_MAX; count = 0; ArrayResize (ideasList, 0, 100); } }; //——————————————————————————————————————————————————————————————————————————————
Para determinar si un agente hijo pertenece al clúster correspondiente, utilizaremos el método K-NN (vecinos k-próximos).
La clase "C_TSEA_clusters" contendrá los siguientes métodos, aparte del método K-Means:
1. Método "VectorDistance":
- Este método calcula la distancia euclídea entre dos vectores "v1" y "v2" representados por arrays de números de tipo "double".
- Utiliza la fórmula de la distancia euclídea:
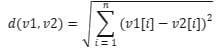 .
. - Se retornará la distancia calculada.
2. Estructura "DistanceIndex":
- La estructura representará un par de valores: la distancia "distance" y el índice "index".
- Se utiliza para almacenar las distancias de un punto a otros puntos y sus índices.
3. Método "BubbleSort":
- Este método clasifica un array de objetos de tipo "DistanceIndex" según la clasificación de burbuja en orden de distancias ascendente.
- La variable temporal "temp" se utilizará para intercambiar elementos del array.
4. El método "KNN" aplica el algoritmo de vecinos k-próximos para la clasificación de los puntos "point":
- Calcula las distancias desde el punto "point" hasta todos los puntos del array "data", clasifica estas distancias y determina si el punto pertenece a uno de los "n_clusters", clústeres basados en los k vecinos más cercanos.
- Se utilizará un array "votes" para contar los votos de cada grupo.
- Se retornará el índice del clúster con mayor número de votos.
//—————————————————————————————————————————————————————————————————————————————— class C_TSEA_clusters { public: double VectorDistance (double &v1 [], double &v2 []) { double distance = 0.0; for (int i = 0; i < ArraySize (v1); i++) { distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]); } return MathSqrt (distance); } struct DistanceIndex { double distance; int index; }; void BubbleSort (DistanceIndex &arr [], int start, int end) { for (int i = start; i < end; i++) { for (int j = start; j < end - i; j++) { if (arr [j].distance > arr [j + 1].distance) { DistanceIndex temp = arr [j]; arr [j] = arr [j + 1]; arr [j + 1] = temp; } } } } int KNN (S_TSEA_Agent &data [], S_TSEA_Agent &point, int k_neighbors, int n_clusters) { int n = ArraySize (data); DistanceIndex distances_indices []; // Calculate the distances from a point to all other points for (int i = 0; i < n; i++) { DistanceIndex dist; dist.distance = VectorDistance (point.c, data [i].c); dist.index = i; ArrayResize (distances_indices, n); distances_indices [i] = dist; } // Sort the distances BubbleSort (distances_indices, 0, n - 1); // Define the cluster for the point int votes []; ArrayResize (votes, n_clusters); ArrayInitialize (votes, 0); for (int j = 0; j < k_neighbors; j++) { int label = data [distances_indices [j].index].label; if (label != -1 && label < n_clusters) { votes [label]++; } } int max_votes = 0; int max_votes_cluster = -1; for (int j = 0; j < n_clusters; j++) { if (votes [j] > max_votes) { max_votes = votes [j]; max_votes_cluster = j; } } return max_votes_cluster; } }; //——————————————————————————————————————————————————————————————————————————————
Vamos a pasar ahora directamente a la descripción de la clase "C_AO_TSEA", que deriva de la clase básica "C_AO" e implementará el algoritmo "Turtle Shell Evolution Algorithm" (TSEA). Campos y métodos de la clase:
1. C_AO_TSEA - constructor que inicializa los campos de la clase. Establecerá el nombre del algoritmo, su descripción y un enlace a un artículo sobre el algoritmo. También establecerá varios parámetros del algoritmo como: el tamaño de la población, el número de clústeres verticales y horizontales, el número de vecinos más próximos y el número máximo de agentes en una celda.
2. SetParams - método que establece los parámetros del algoritmo basándose en los valores de el array "params".
3. Init - método que inicializa el algoritmo. Admite rangos de búsqueda mínimo y máximo, paso de búsqueda y número de épocas.
4. Los métodos "Moving", "Revision" son los métodos principales del TSEA que implementan su lógica básica.
5. Los campos "vClusters", "hClusters", "neighbNumb" y "maxAgentsInCell" son parámetros de algoritmo que se establecen en el constructor y pueden modificarse usando el método "SetParams".
6. Las arrays "agent", "cell" y "clusters" son las estructuras de datos utilizadas por el algoritmo. Contienen información sobre agentes, células y clústeres, respectivamente.
7. El objeto "km" de la clase "C_TSEA_clusters" se usa para realizar operaciones de clusterización.
8. Los campos privados "minFval", "stepF", "epochs" y "epochsNow" son variables internas. No hemos previsto que se acceda a ellas desde fuera de la clase.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_TSEA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_TSEA () { } C_AO_TSEA () { ao_name = "TSEA"; ao_desc = "Turtle Shell Evolution Algorithm"; ao_link = "https://www.mql5.com/ru/articles/14789"; popSize = 100; //population size vClusters = 3; //number of vertical clusters hClusters = 10; //number of horizontal clusters neighbNumb = 5; //number of nearest neighbors maxAgentsInCell = 3; //max agents in cell ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "vClusters"; params [1].val = vClusters; params [2].name = "hClusters"; params [2].val = hClusters; params [3].name = "neighbNumb"; params [3].val = neighbNumb; params [4].name = "maxAgentsInCell"; params [4].val = maxAgentsInCell; } void SetParams () { popSize = (int)params [0].val; vClusters = (int)params [1].val; hClusters = (int)params [2].val; neighbNumb = (int)params [3].val; maxAgentsInCell = (int)params [4].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- int vClusters; //number of vertical clusters int hClusters; //number of horizontal clusters int neighbNumb; //number of nearest neighbors int maxAgentsInCell; S_TSEA_Agent agent []; S_TSEA_vertical cell []; S_Cluster clusters []; C_TSEA_clusters km; private: //------------------------------------------------------------------- double minFval; double stepF; int epochs; int epochsNow; }; //——————————————————————————————————————————————————————————————————————————————
El método "Init" de la clase "C_AO_TSEA" inicializará el algoritmo TSEA. Aquí vemos una descripción detallada de su funcionamiento:
1. StandardInit (rangeMinP, rangeMaxP, rangeStepP) - el método se llamará para la inicialización estándar del algoritmo. Admite rangos de búsqueda mínimo y máximo y paso de búsqueda. Si la inicialización falla, el método retornará "false".
2. ArrayResize (agent, popSize) - cambia el tamaño del array "agent" al tamaño de población "popSize". A continuación, se llamará al método "Init(coords)" para cada agente, que inicializará el agente.
3. ArrayResize (clusters, hClusters) - cambia el tamaño del array "clusters" al número de clústeres horizontales "hClusters". Luego se llamará al método "Init(coords)" para cada clúster, que inicializa el clúster.
4. ArrayResize (cell, vClusters) - cambia el tamaño del array "cell" al número de clústeres verticales "vClusters". Después el array "cell[i].cell" y el array de agentes de cada celda se inicializarán para cada celda.
5. "minFval = DBL_MAX", "stepF = 0.0", "epochs = epochsP", "epochsNow = 0". Esta es la inicialización de las variables internas del algoritmo.
6. Al final, el método retornará "true", lo cual indicará que la inicialización se ha realizado correctamente.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSEA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (clusters, hClusters); for (int i = 0; i < hClusters; i++) clusters [i].Init (coords); ArrayResize (cell, vClusters); for (int i = 0; i < vClusters; i++) { ArrayResize (cell [i].cell, hClusters); for (int c = 0; c < hClusters; c++) ArrayResize (cell [i].cell [c].agent, 0, maxAgentsInCell); } minFval = DBL_MAX; stepF = 0.0; epochs = epochsP; epochsNow = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
El método "Moving" de la clase "C_AO_TSEA" implementará la lógica básica del movimiento de los agentes en el algoritmo TSEA. Breve descripción de los pasos básicos:
1. Inicialización de la población:
- Si se trata de la primera iteración (revision == false), se generarán individuos aleatorios para la población.
- De lo contrario, se producirá una renovación de la población basada en las soluciones existentes.
2. Renovación de la población:
- Para cada clúster (vClusters x hClusters), se encontrará la mejor solución.
- Las nuevas soluciones se formarán de la siguiente manera:
- Con una probabilidad de 0,5, se copiará la mejor solución de un clúster aleatorio con cierto desplazamiento
- Con una probabilidad de 0,2, la nueva solución se formará como la media entre dos soluciones aleatorias de clústers diferentes
- Las nuevas coordenadas de la solución se generarán utilizando una distribución escalonada para mantener la proximidad a las mejores soluciones.
3. Renovación de agentes (individuos) en la población
Este método hace realidad la idea básica de la evolución del caparazón de tortuga, en el que las mejores soluciones se vuelven más "duras" y se sitúan más cerca de la superficie exterior, mientras que las soluciones menos exitosas permanecen "blandas" y se sitúan en el interior. La clusterización de soluciones y el guardado de las opciones menos acertadas aportarán flexibilidad y adaptabilidad al algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSEA::Moving () { epochsNow++; //---------------------------------------------------------------------------- //1. Generate random individuals for the population if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } return; } //---------------------------------------------------------------------------- int vPos = 0; int hPos = 0; int pos = 0; int size = 0; double val = 0.0; double rnd = 0.0; double min = 0.0; double max = 0.0; for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { size = ArraySize (cell [v].cell [h].agent); if (size > 0) { max = -DBL_MAX; pos = -1; for (int c = 0; c < size; c++) { if (cell [v].cell [h].agent [c].f > max) { max = cell [v].cell [h].agent [c].f; pos = c; cell [v].cell [h].indBest = c; } } } } } for (int i = 0; i < popSize; i++) { if (u.RNDprobab () < 0.8) { while (true) { rnd = u.RNDprobab (); rnd = (-rnd * rnd + 1.0) * vClusters; vPos = (int)rnd; if (vPos > vClusters - 1) vPos = vClusters - 1; hPos = u.RNDminusOne (hClusters); size = ArraySize (cell [vPos].cell [hPos].agent); if (size > 0) break; } pos = u.RNDminusOne (size); if (u.RNDprobab () < 0.5) pos = cell [vPos].cell [hPos].indBest; for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.6) val = cell [vPos].cell [hPos].agent [pos].c [c]; else val = cB [c]; double dist = (rangeMax [c] - rangeMin [c]) * 0.1; min = val - dist; if (min < rangeMin [c]) min = rangeMin [c]; max = val + dist; if (max > rangeMax [c]) max = rangeMax [c]; val = u.PowerDistribution (val, min, max, 30); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } else { int size2 = 0; int hPos2 = 0; int pos2 = 0; while (true) { rnd = u.RNDprobab (); rnd = (-rnd * rnd + 1.0) * vClusters; vPos = (int)rnd; if (vPos > vClusters - 1) vPos = vClusters - 1; hPos = u.RNDminusOne (hClusters); size = ArraySize (cell [vPos].cell [hPos].agent); hPos2 = u.RNDminusOne (hClusters); size2 = ArraySize (cell [vPos].cell [hPos2].agent); if (size > 0 && size2 > 0) break; } pos = u.RNDminusOne (size); pos2 = u.RNDminusOne (size2); for (int c = 0; c < coords; c++) { val = (cell [vPos].cell [hPos ].agent [pos ].c [c] + cell [vPos].cell [hPos2].agent [pos2].c [c]) * 0.5; a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = a [i].c [c]; } } } } //——————————————————————————————————————————————————————————————————————————————El método "Revision" de la clase "C_AO_TSEA" implementará el paso de redistribución de las secciones del caparazón de tortuga en el algoritmo TSEA.
El método es responsable del proceso de revisión (actualización) de la población de agentes y de la actualización de la mejor solución global.
Los principales pasos de esta parte del algoritmo serán:
2. Etiquetamos los agentes en clústeres verticales "labelClustV" según su aptitud.
3. Si se trata de la primera iteración (revision == false), la clusterización de agentes se inicializará utilizando el algoritmo K-Means.
4. Si no es la primera iteración, se realizará lo siguiente:
- Recogemos todos los agentes en un única array de datos.
- Para cada agente de la población, determinamos su "etiqueta" de clúster horizontal usando el algoritmo de vecinos K-próximos.
- Cada 50 épocas, actualizamos la estructura de "celdas" que almacena los agentes divididos en clústeres.
5. Colocamos cada agente en la celda correspondiente. Si la celda ya está llena, el agente sustituirá al agente de la celda con la adaptabilidad más baja (o más alta, si la celda está en un nivel inferior).
La idea principal de esta etapa consiste en mantener una estructura de caparazón en la que las mejores soluciones se sitúen más cerca de la superficie exterior y las menos acertadas, en el interior. La clusterización de los agentes y la actualización dinámica de la estructura del caparazón aportarán flexibilidad y adaptabilidad al algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSEA::Revision () { //get fitness-------------------------------------------------- int pos = -1; for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; if (a [i].f > fB) { fB = a [i].f; pos = i; } if (a [i].f < minFval) minFval = a [i].f; } if (pos != -1) ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY); stepF = (fB - minFval) / vClusters; //Vertical layout of the child population----------------------------------- for (int i = 0; i < popSize; i++) { if (agent [i].f == fB) agent [i].labelClustV = vClusters - 1; else { agent [i].labelClustV = int((agent [i].f - minFval) / stepF); if (agent [i].labelClustV > vClusters - 1) agent [i].labelClustV = vClusters - 1; } } //---------------------------------------------------------------------------- if (!revision) { km.KMeansPlusPlusInit (agent, popSize, clusters); km.KMeans (agent, popSize, clusters); revision = true; } //---------------------------------------------------------------------------- else { static S_TSEA_Agent data []; ArrayResize (data, 0, 1000); int size = 0; for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { for (int c = 0; c < ArraySize (cell [v].cell [h].agent); c++) { size++; ArrayResize (data, size); data [size - 1] = cell [v].cell [h].agent [c]; } } } for (int i = 0; i < popSize; i++) { agent [i].label = km.KNN (data, agent [i], neighbNumb, hClusters); } if (epochsNow % 50 == 0) { for (int v = 0; v < vClusters; v++) { for (int h = 0; h < hClusters; h++) { ArrayResize (cell [v].cell [h].agent, 0); } } for (int i = 0; i < ArraySize (data); i++) { if (data [i].f == fB) data [i].labelClustV = vClusters - 1; else { data [i].labelClustV = int((data [i].f - minFval) / stepF); if (data [i].labelClustV > vClusters - 1) data [i].labelClustV = vClusters - 1; } int v = data [i].labelClustV; int h = data [i].label; int size = ArraySize (cell [v].cell [h].agent) + 1; ArrayResize (cell [v].cell [h].agent, size); cell [v].cell [h].agent [size - 1] = data [i]; } } } //Place the population in the shell------------------------------------ for (int i = 0; i < popSize; i++) { int v = agent [i].labelClustV; int h = agent [i].label; int size = ArraySize (cell [v].cell [h].agent); int pos = 0; int posMin = 0; int posMax = 0; if (size >= maxAgentsInCell) { double minF = DBL_MAX; double maxF = -DBL_MAX; for (int c = 0; c < maxAgentsInCell; c++) { if (cell [v].cell [h].agent [c].f < minF) { minF = cell [v].cell [h].agent [c].f; posMin = c; } if (cell [v].cell [h].agent [c].f > maxF) { maxF = cell [v].cell [h].agent [c].f; posMax = c; } } if (v == 0) { if (agent [i].f < minF) { pos = posMin; } else { pos = posMax; } } else pos = posMin; } else { ArrayResize (cell [v].cell [h].agent, size + 1); pos = size; } cell [v].cell [h].agent [pos] = agent [i]; } } //——————————————————————————————————————————————————————————————————————————————
3. Resultados de las pruebas
Impresión de los resultados del algoritmo de evolución del caparazón de tortuga TSEA:
TSEA|Turtle Shell Evolution Algorithm|100.0|3.0|10.0|5.0|3.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.811921100517765
25 Hilly's; Func runs: 10000; result: 0.5537631430428238
500 Hilly's; Func runs: 10000; result: 0.2813575513298344
=============================
5 Forest's; Func runs: 10000; result: 0.9564485273109922
25 Forest's; Func runs: 10000; result: 0.481362270824773
500 Forest's; Func runs: 10000; result: 0.181400891410298
=============================
5 Megacity's; Func runs: 10000; result: 0.6676923076923076
25 Megacity's; Func runs: 10000; result: 0.3633846153846153
500 Megacity's; Func runs: 10000; result: 0.11670769230769343
=============================
All score: 4.41404 (49.04%)
La puntuación total de todas las funciones de prueba es de 4,41404, lo que se corresponde con el 49,04% de la solución óptima teórica.
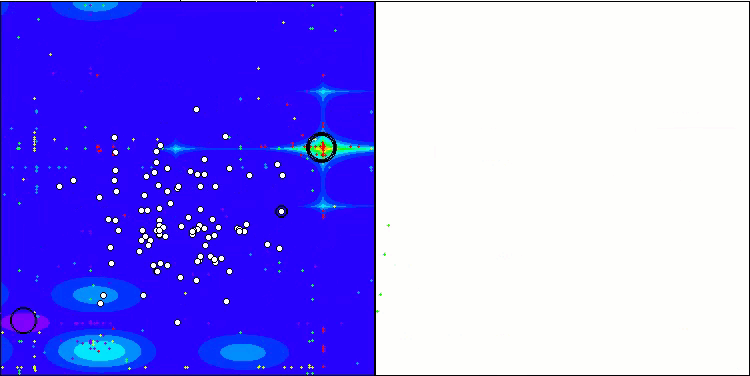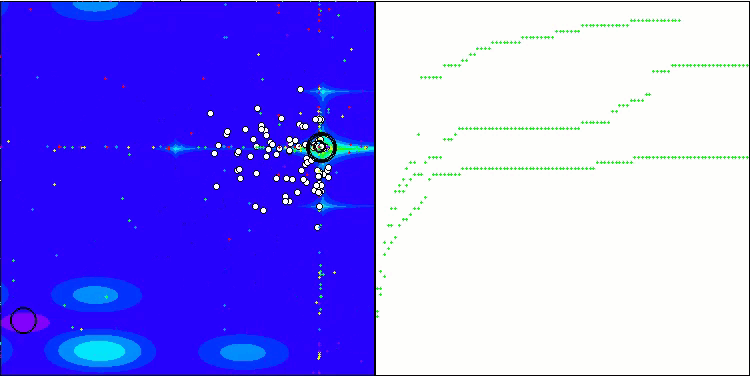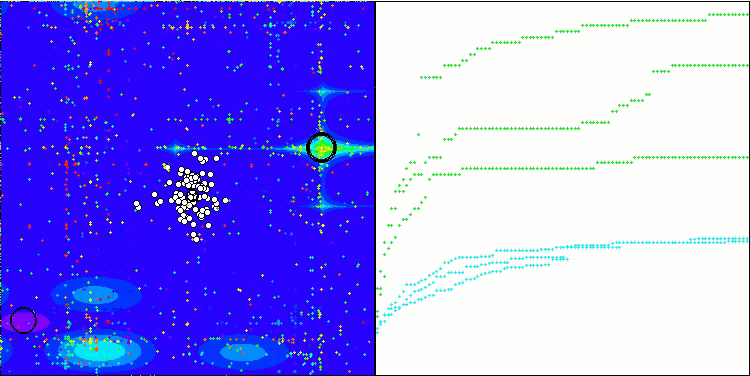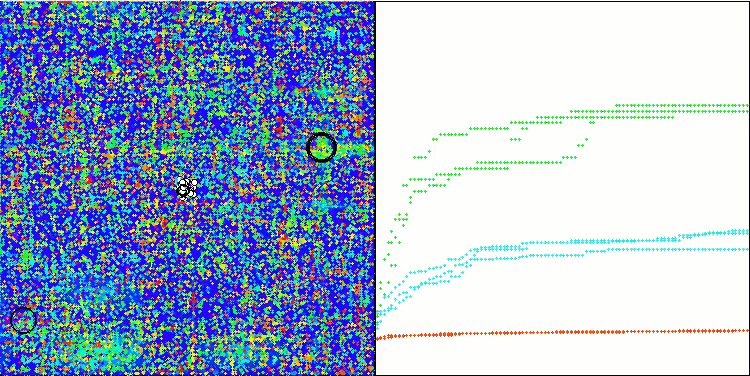
La visualización del funcionamiento del banco de pruebas demuestra la buena convergencia del algoritmo. En todas las funciones de prueba existe una cierta dispersión de trayectorias en el gráfico de convergencia, pero al aumentar los grados de libertad, esta dispersión disminuye. El uso de la clusterización en el algoritmo, así como el mantenimiento de un número constante de agentes en cada celda, permite al algoritmo explorar eficazmente partes significativas de la función de aptitud.
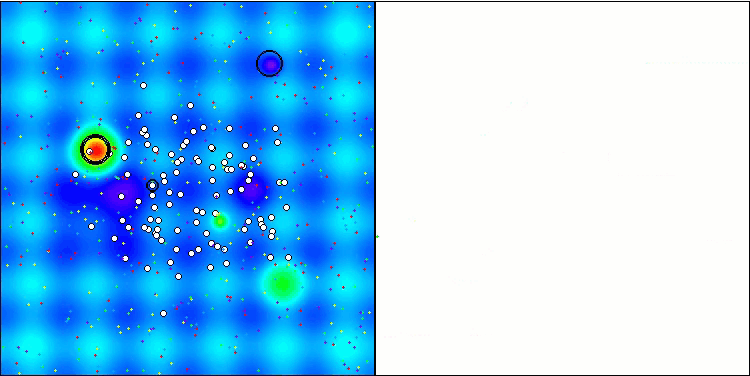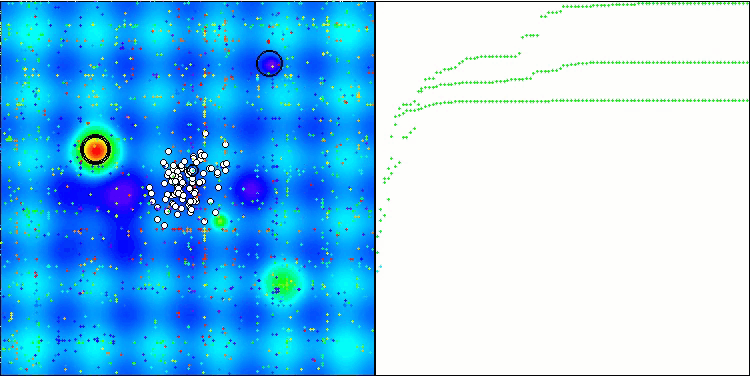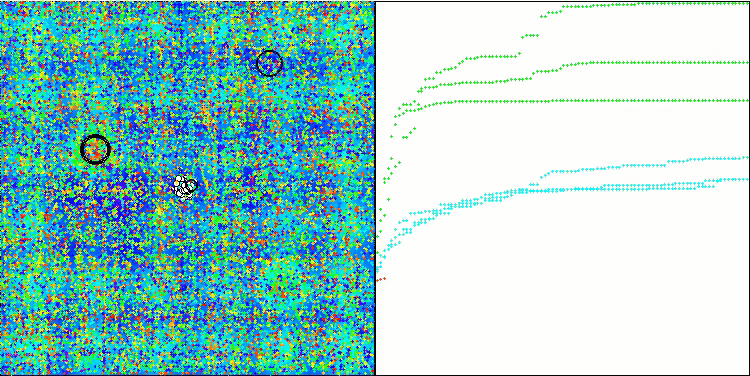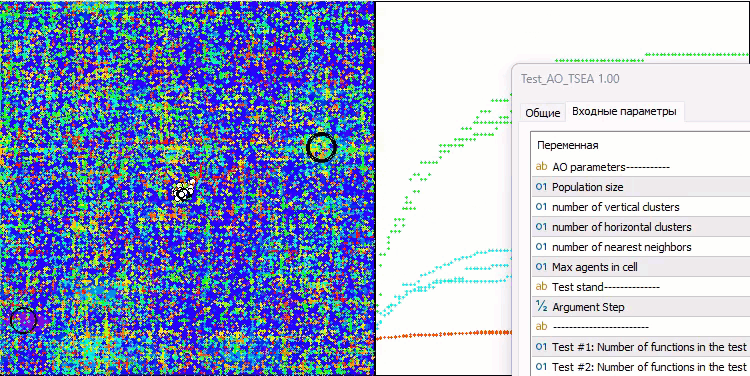
TSEA en la función de prueba Hilly.
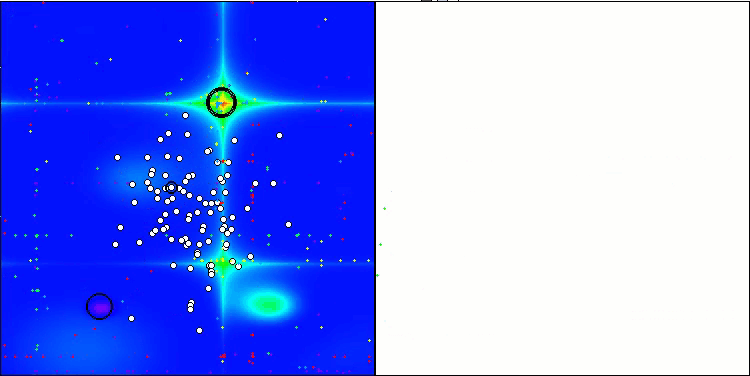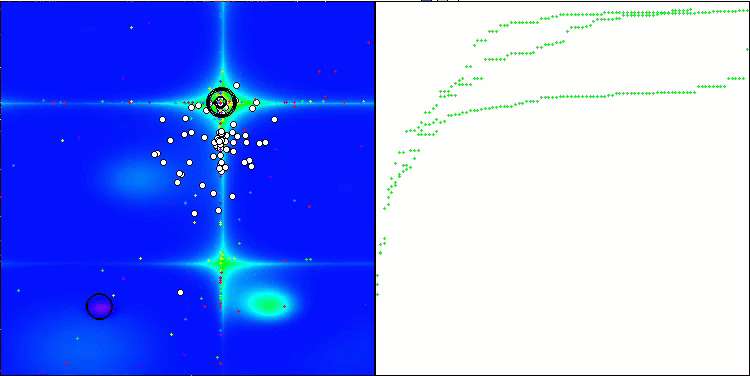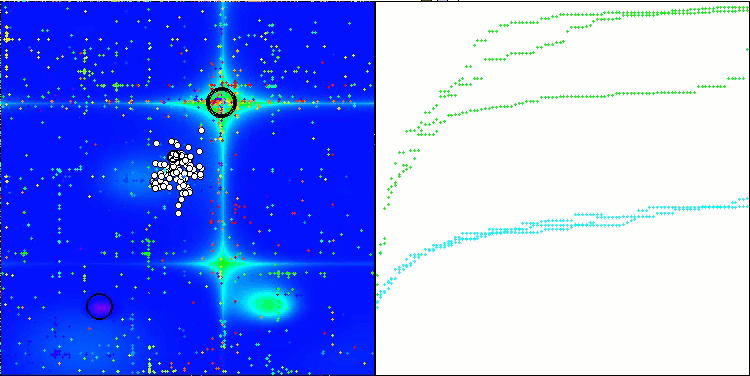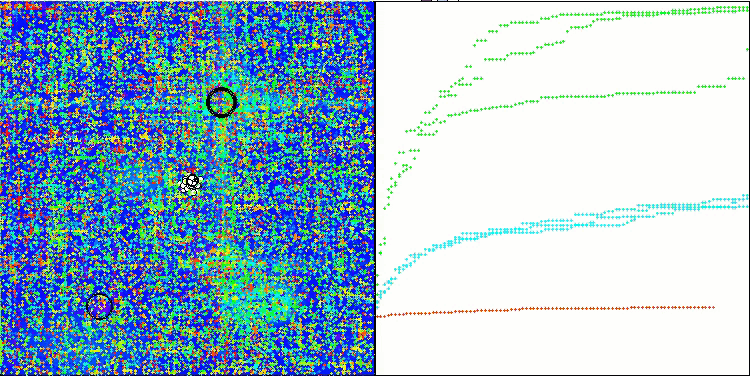
TSEA en la función de prueba Forest.
TSEA en la función de prueba Megacity.
El algoritmo, tras ser verificado en funciones de prueba, ha ocupado un meritorio 6º puesto en lo alto de la tabla de clasificación final.
№ | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % de MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99992 | 0,99484 | 0,50483 | 2,49959 | 1,00000 | 0,99975 | 0,32054 | 2,32029 | 0,90667 | 0,96400 | 0,23035 | 2,10102 | 6,921 | 76,90 |
| 2 | (P+O)ES | (P+O) evolution strategies | 0,99934 | 0,91895 | 0,56297 | 2,48127 | 1,00000 | 0,93522 | 0,39179 | 2,32701 | 0,83167 | 0,64433 | 0,21155 | 1,68755 | 6,496 | 72,18 |
| 3 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 4 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 5 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 6 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 7 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 8 | BSA | bird swarm algorithm | 0,90857 | 0,73661 | 0,25767 | 1,90285 | 0,90437 | 0,81619 | 0,16401 | 1,88457 | 0,61692 | 0,54154 | 0,10951 | 1,26797 | 5,055 | 56,17 |
| 9 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 10 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 11 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 12 | BSO | brain storm optimization | 0,91301 | 0,56222 | 0,30047 | 1,77570 | 0,97162 | 0,57162 | 0,23449 | 1,77772 | 0,60462 | 0,27138 | 0,12011 | 0,99611 | 4,550 | 50,55 |
| 13 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 14 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 15 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 16 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 17 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 18 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 19 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 20 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 21 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 22 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 23 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 24 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 25 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 26 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 27 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 28 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 29 | PSO | particle swarm Optimization | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 30 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 31 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 32 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 33 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 34 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 35 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 36 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 37 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Conclusiones
La idea de un algoritmo de optimización basado en el crecimiento del caparazón de las tortugas ha resultado bastante interesante; incluso animales tan lentos pueden servir de inspiración y ejemplo de soluciones "técnicas" para las que la naturaleza es inagotable. Basándonos en las pruebas realizadas con el algoritmo TSEA (Turtle Shell Evolution Algorithm), podemos destacar sus peculiaridades.
El almacenamiento de las soluciones menos exitosas es una característica única del algoritmo. Esto se manifiesta en el hecho de que las variantes menos exitosas queden retenidas en la capa interna del caparazón. Este enfoque mantiene la diversidad de la población y evita la convergencia prematura a óptimos locales. Resulta importante recordar que un mínimo local que parece ser la peor solución puede encontrarse cerca del óptimo global, por lo que seguir explorando su vecindad tiene sentido. Aunque el algoritmo puede explorar estas zonas con menos intensidad que otros lugares más prometedores, siguen suponiendo un foco de atención.
La división de las soluciones en grupos a lo largo de la vertical, imitando las capas del caparazón, y de la horizontal, imitando los patrones característicos de la superficie, nos permite asignar regiones del espacio de soluciones con bastante eficacia y estudiar estas por separado. Al mismo tiempo, el patrón del caparazón sigue siendo móvil y puede cambiar y adaptarse a la superficie de la función de aptitud.
La división del caparazón en capas permite que se formen nuevas soluciones dentro de cada capa. Las capas duras superiores no interactúan con las capas blandas inferiores, y viceversa. Esto se asemeja al proceso de crecimiento del caparazón en una tortuga viva, pero con la diferencia de que la zona dura de la capa inferior puede pasar a las capas superiores, debido a la reclusterización periódica. Podemos compararlo con deshacerse de un viejo caparazón y formar uno nuevo, más fuerte y mejor.
El algoritmo muestra un buen rendimiento en tareas con diferente número de dimensiones (escalabilidad), lo que indica su flexibilidad.
En general, el TSEA supone un enfoque interesante que combina los mecanismos de los algoritmos evolutivos y la clusterización. No obstante, estoy seguro de que el potencial del algoritmo dista mucho de haberse agotado. En este punto, solo se han utilizado unas pocas formas de crear nuevas soluciones de entre la enorme variedad comentada anteriormente en los artículos. El algoritmo sigue siendo mi objetivo y está abierto a nuevas mejoras. Tal vez sirva de base para que surjan nuevas modificaciones, de forma similar a lo ocurrido con el PSO y otros algoritmos bien conocidos.
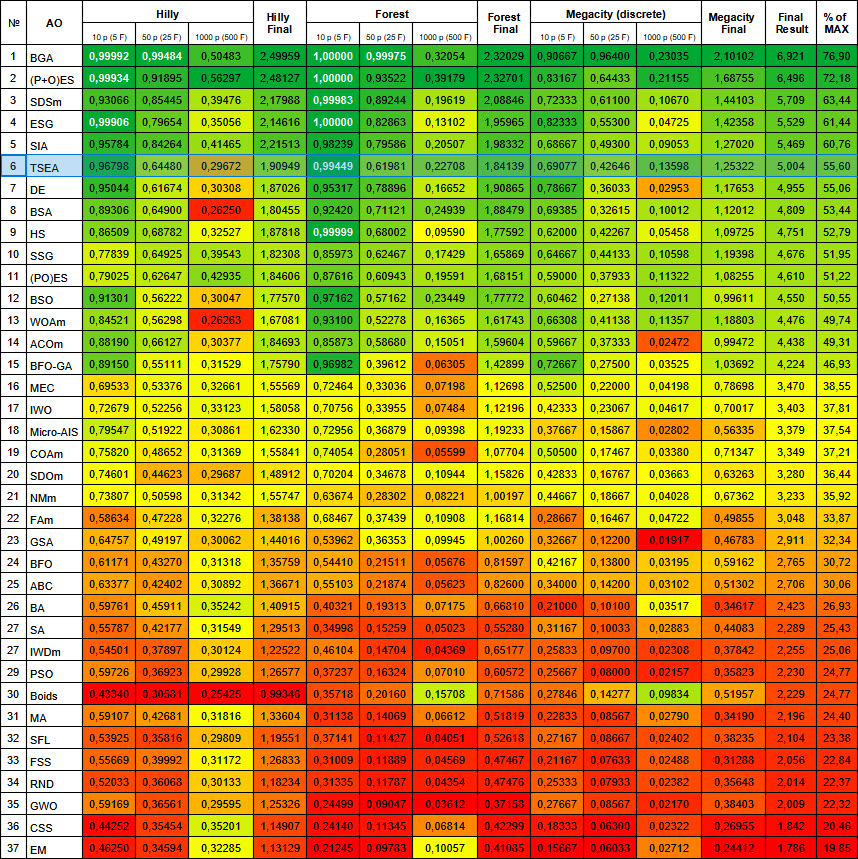
Figura 3. Gradación por colores de los algoritmos según sus respectivas pruebas. Los resultados superiores o iguales a 0,99 aparecen resaltados en blanco.
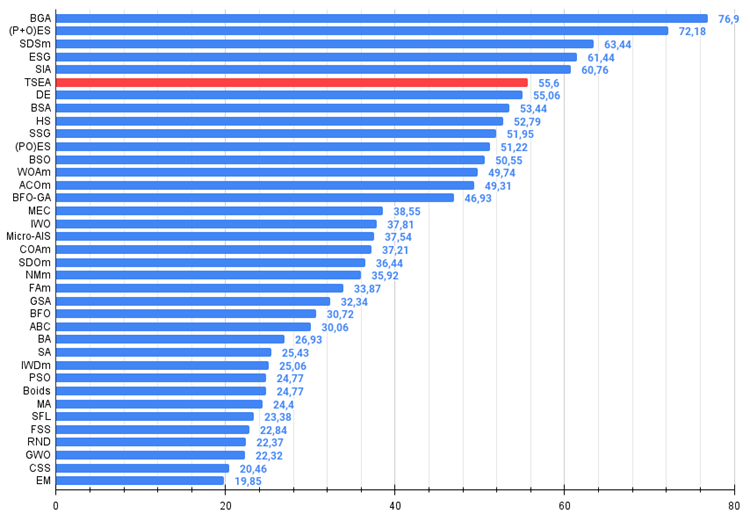
Figura 4. Histograma con los resultados de las pruebas de los algoritmos (en una escala de 0 a 100, cuanto mayor, mejor),
donde 100 es el máximo resultado teórico posible; hay un script para calcular la tabla de puntuación en el archivo).
Ventajas y desventajas del algoritmo evolutivo de caparazón de tortuga (TSEA):
Ventajas:
- Buena convergencia en distintos tipos de funciones
- Número reducido de parámetros externos
Desventajas:
- Gran dispersión de resultados en funciones de pequeña dimensionalidad
- Alta exigencia de recursos informáticos
Adjuntamos al artículo un archivo con las versiones actuales de los códigos de los algoritmos. El autor de este artículo no se responsabiliza de la exactitud absoluta de la descripción de los algoritmos canónicos, muchos de ellos han sido modificados para mejorar las capacidades de búsqueda. Las conclusiones y juicios presentados en los artículos se basan en los resultados de los experimentos realizados.
github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
CodeBase: https://www.mql5.com/es/code/49355
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/14789
 Creación de una interfaz gráfica de usuario interactiva en MQL5 (Parte 1): Creación del panel
Creación de una interfaz gráfica de usuario interactiva en MQL5 (Parte 1): Creación del panel
 Desarrollamos un asesor experto multidivisa (Parte 10): Creación de objetos a partir de una cadena
Desarrollamos un asesor experto multidivisa (Parte 10): Creación de objetos a partir de una cadena
 Características del Wizard MQL5 que debe conocer (Parte 25): Pruebas y operaciones en múltiples marcos temporales
Características del Wizard MQL5 que debe conocer (Parte 25): Pruebas y operaciones en múltiples marcos temporales
 Creación de un modelo de restricción de tendencia de velas (Parte 5): Sistema de notificaciones (Parte III)
Creación de un modelo de restricción de tendencia de velas (Parte 5): Sistema de notificaciones (Parte III)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso