
Algoritmo de Otimização Aritmética (AOA): O caminho do AOA até o SOA (Simple Optimization Algorithm)
Conteúdo
Introdução
O Algoritmo de Otimização Aritmética (Arithmetic Optimization Algorithm, AOA) é um método original baseado em operações aritméticas simples, como adição, subtração, multiplicação e divisão. Ele busca soluções ótimas em uma variedade de problemas por meio do uso desses princípios matemáticos básicos. Desenvolvido por uma equipe de pesquisadores, incluindo Laith Abualigah, o AOA foi apresentado pela primeira vez em 2021. Esse algoritmo pertence à classe dos métodos metaheurísticos (algoritmos de alto nível), que visam buscar, gerar e selecionar probabilisticamente entre várias heurísticas capazes de fornecer soluções suficientemente boas em tempo razoável para problemas complexos de otimização, nos quais métodos exatos podem ser ineficazes ou inviáveis.
O que me atraiu nesse método foi a ideia simples e, ao mesmo tempo, elegante de aplicar operadores aritméticos absolutamente elementares. A conexão entre essas ações matemáticas básicas e os enfoques metaheurísticos cria uma interação que permite resolver problemas complexos de otimização. Os métodos metaheurísticos aplicados no AOA incluem alguns princípios-chave:
1. Abordagem populacional. O AOA utiliza uma população de soluções, o que permite cobrir de forma mais ampla o espaço de soluções possíveis. Isso ajuda a evitar ótimos locais e amplia os horizontes da busca.
2. Aleatoriedade e estocasticidade. A inclusão de elementos aleatórios no processo de busca ajuda os algoritmos a não ficarem presos em ótimos locais e garante uma exploração mais completa do espaço de soluções, o que aumenta a chance de encontrar o ótimo global.
3. Equilíbrio entre diversificação e intensificação. Assim como muitos outros algoritmos metaheurísticos, o AOA busca um equilíbrio entre explorar novas áreas do espaço de soluções e intensificar a busca nas soluções já conhecidas como eficazes. Isso é feito através da aplicação de operações aritméticas para atualizar as posições das soluções.
Assim, o AOA é um exemplo marcante de algoritmo metaheurístico que utiliza de forma eficaz os princípios da abordagem populacional, da aleatoriedade e do equilíbrio entre diversificação e intensificação para resolver problemas de otimização. No entanto, sua eficácia específica em encontrar soluções ótimas em espaços complexos e multidimensionais será discutida após sua implementação e testes.
Implementação do algoritmo
A ideia principal do AOA está no uso do comportamento distributivo dos operadores aritméticos para buscar soluções ótimas. O algoritmo se caracteriza por princípios simples, poucos parâmetros e fácil implementação. Ele utiliza as propriedades distributivas dos quatro operadores aritméticos básicos da matemática, a saber: Multiplicação (Mε × ε), Divisão (Dε ÷ ε), Subtração (Sε − ε) e Adição (Aε + ε). No AOA, a população inicial é gerada aleatoriamente no intervalo [U; L], onde U e L representam, respectivamente, os limites superior e inferior do espaço de busca da função objetivo, utilizando a seguinte equação:
x = L + (U − L) × δ, onde x representa uma solução da população e δ é uma variável aleatória com valores entre [0, 1].
A cada iteração, a escolha da estratégia de diversificação ou intensificação, ou seja, a escolha entre os dois grupos de operadores, (divisão; multiplicação) ou (subtração; adição), depende do resultado da função MoA (math optimizer accelerated), que é, na essência, um valor probabilístico calculado e que varia a cada iteração, sendo computado pela equação:
MoA(t) = Min + t × (Max − Min) ÷ Maxt, onde MoA(t) representa o resultado funcional na iteração t, t indica a iteração atual dentro do intervalo de 1 até o número máximo de iterações (Maxt). O valor mínimo possível de MoA é representado por Min, e o valor máximo por Max, ambos sendo parâmetros externos do algoritmo.
Nas quatro fórmulas que envolvem operadores aritméticos, é utilizado o coeficiente MoP (math optimizer), calculado da seguinte forma:
MoP(t) = 1 − (t ÷ Maxt)^(1 ÷ θ), onde MoP(t) representa o valor da função MoP na iteração t. θ é um parâmetro crítico que controla a eficácia da intensificação ao longo das iterações. No trabalho original dos autores do algoritmo, esse valor foi definido como 5.
A figura 1 abaixo apresenta os gráficos da dependência de MoA e MoP em relação à iteração atual. Os gráficos mostram que, a cada iteração, o MoA cresce linearmente, o que significa um aumento na probabilidade de escolha do grupo de operadores (subtração; adição), enquanto a probabilidade de escolha do grupo de operadores (divisão; multiplicação) diminui proporcionalmente. Em contrapartida, o coeficiente MoP diminui de forma não linear, reduzindo assim o incremento aplicado à posição atual dos agentes na população, o que indica um maior grau de refinamento das soluções durante o processo de otimização.
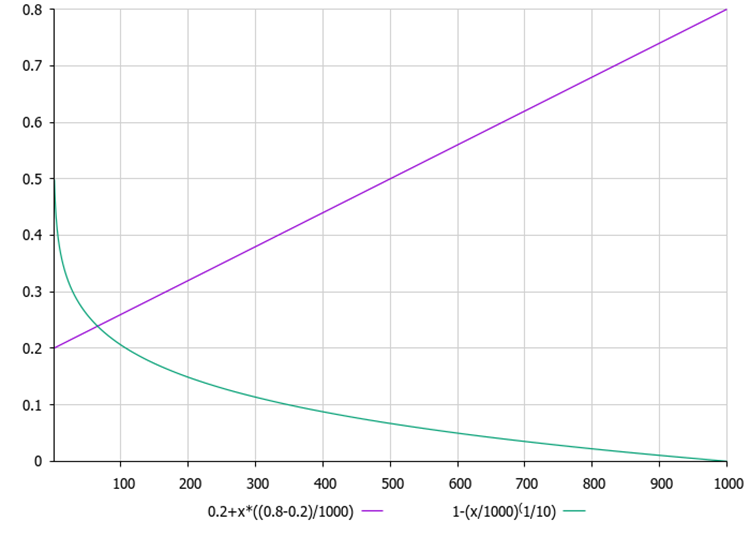
Figura 1. O gráfico roxo representa a probabilidade MoA, enquanto o gráfico verde representa o coeficiente MoP
Diversificação ou busca global no AOA é realizada com o uso de estratégias baseadas nos operadores de Divisão (D) e Multiplicação (M), quando a probabilidade MoA é atendida, formulada da seguinte maneira, onde os seguintes operadores são executados com igual probabilidade:
xi,j(t+1) = best(xj) ÷ (MoPr + 𝜖) × ((Uj − Lj) × 𝜇 + Lj), se rand2 < 0.5;
caso contrário:
xi,j(t+1) = best(xj) × (MoPr) × ((Uj − Lj) × 𝜇 + Lj), onde xi(t+1) representa a i-ésima solução na iteração (t+1), x(i,j)(t) representa a j-ésima posição do i-ésimo indivíduo na geração atual, best(xj) representa a j-ésima posição da melhor solução encontrada até o momento, ε é um pequeno número positivo, e os limites superior e inferior dos valores da j-ésima posição são representados como Uj e Lj, respectivamente. O parâmetro de controle μ foi definido no nível de 0.5.
Se a probabilidade MoA não for atendida, então o AOA executa a estratégia de intensificação (refinamento da solução), que foi desenvolvida usando os operadores de Subtração (S) ou Adição (A). Aqui, μ também é uma constante, fixada no nível de 0.5 conforme o projeto dos autores.
xi,j(t+1) = best(xj) − (MoPr) × ((Uj − Lj) × 𝜇 + Lj), se rand3 < 0.5
xi,j(t+1) = best(xj) + (MoPr) × ((Uj − Lj) × 𝜇 + Lj), caso contrário.
No AOA, os parâmetros 𝜇 e θ são extremamente importantes, pois participam do equilíbrio entre diversificação e intensificação. Manter esse equilíbrio é, geralmente, uma tarefa bastante desafiadora. No trabalho original do AOA, o valor de 𝜇 foi fixado em 0.5 tanto para diversificação quanto para intensificação. Já o parâmetro θ, que influencia a eficácia da intensificação ao longo das iterações, foi definido como 5. Os autores realizaram experimentos com diferentes valores de 𝜇 e θ e descobriram que 𝜇 = 0.5 e θ = 5 forneceram, com mais frequência, os melhores resultados para funções de teste unimodais e multimodais em diversas dimensionalidades.
Agora, vamos escrever o pseudocódigo do algoritmo AOA:
aumentar o número da época em 1
// Inicialização inicial
SE for a primeira execução ENTÃO
PARA cada partícula na população:
PARA cada coordenada:
definir uma posição aleatória dentro do intervalo permitido
converter a posição para um valor discreto
marcar que a inicialização foi concluída
encerrar a função
FIM SE
// Processo principal de otimização
calcular MoA = minMoA + númeroÉpoca * ((maxMoA − minMoA) ÷ totalÉpocas)
calcular MoP = 1 − (númeroÉpoca ÷ totalÉpocas)^(1/θ)
// Fase de diversificação do espaço de soluções
PARA cada partícula na população:
PARA cada coordenada:
gerar três valores aleatórios (rand1, rand2, rand3)
obter o melhor valor conhecido para essa coordenada
SE rand1 < MoAc ENTÃO
SE rand2 > 0.5 ENTÃO
atualizar a posição usando Divisão
SENÃO
atualizar a posição usando Multiplicação
FIM SE
SENÃO
SE rand3 > 0.5 ENTÃO
atualizar a posição usando Subtração
SENÃO
atualizar a posição usando Adição
FIM SE
FIM SE
converter a nova posição para um valor discreto permitido
Atualizar a melhor solução encontrada
Agora passamos à implementação do código. A classe "C_AO_AOA" representa a implementação do algoritmo AOA e é destinada à resolução de tarefas de otimização utilizando o método baseado em operações aritméticas. Métodos públicos:
1. O método "SetParams ()" define os valores dos parâmetros a partir do array "params". Esse método permite alterar os parâmetros do algoritmo após sua inicialização.
2. O método "Init ()":
- Inicializa o algoritmo, recebendo como entrada os limites mínimo e máximo da busca, o passo da busca e a quantidade de épocas.
- Retorna "true", se a inicialização foi bem-sucedida, caso contrário retorna "false".
3. O método "Moving ()" — realiza o deslocamento das partículas no espaço de soluções. Esse método implementa a lógica de atualização das posições das partículas com base nos parâmetros definidos e no estado atual.
4. O método "Revision()" — realiza a revisão das posições atuais das partículas, atualizando o melhor valor encontrado da função e as coordenadas da partícula correspondente.
Campos privados, parâmetros da classe:
- minT — valor mínimo da probabilidade MoA.
- maxT — valor máximo da probabilidade MoA.
- θ — parâmetro que influencia o equilíbrio entre diversificação e intensificação.
- μ — parâmetro utilizado para controlar as mudanças nas posições das partículas (amplitude de deslocamento).
- ϵ — número pequeno para evitar divisão por zero.
Informações sobre o estado do algoritmo:
- epochs — quantidade total de épocas pelas quais o algoritmo irá passar.
- epochNow — época atual, usada para acompanhar o progresso do algoritmo, influencia a probabilidade MoA e o coeficiente MoP.
A classe "C_AO_AOA" implementa os principais componentes do algoritmo AOA, incluindo a inicialização, o deslocamento das partículas e a revisão.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_AOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_AOA () { } C_AO_AOA () { ao_name = "AOA"; ao_desc = "Arithmetic Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16364"; popSize = 50; // Размер популяции minT = 0.1; // Минимальное значение T maxT = 0.9; // Максимальное значение T θ = 10; // Параметр θ μ = 0.01; // Параметр μ ArrayResize (params, 5); // Изменение размера массива параметров // Инициализация параметров params [0].name = "popSize"; params [0].val = popSize; params [1].name = "minT"; params [1].val = minT; params [2].name = "maxT"; params [2].val = maxT; params [3].name = "θ"; params [3].val = θ; params [4].name = "μ"; params [4].val = μ; } void SetParams () // Метод для установки параметров { popSize = (int)params [0].val; // Установка размера популяции minT = params [1].val; // Установка минимального T maxT = params [2].val; // Установка максимального T θ = params [3].val; // Установка параметра θ μ = params [4].val; // Установка параметра μ } bool Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0); // Количество эпох void Moving (); // Метод перемещения частиц void Revision (); // Метод ревизии //---------------------------------------------------------------------------- double minT; // Минимальное значение T double maxT; // Максимальное значение T double θ; // Параметр θ double μ; // Параметр μ double ϵ; // Параметр для предотвращения деления на ноль private: //------------------------------------------------------------------- int epochs; // Общее количество эпох int epochNow; // Текущая эпоха }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" da classe "C_AO_AOA" é responsável por inicializar o algoritmo de otimização, configurando os parâmetros do intervalo de busca, os passos e a quantidade de épocas durante as quais a otimização será executada. A lógica de funcionamento do método:
1. O método chama primeiro o "StandardInit", que inicializa os parâmetros padrão do algoritmo. Se essa inicialização falhar, o método "Init" encerra imediatamente a execução e retorna "false".
2. Definição de parâmetros:
- Define o número total de épocas "epochs" com base no parâmetro recebido "epochsP".
- Inicializa a época atual "epochNow" com o valor "0".
- Define o valor de "ϵ" (valor pequeno para evitar divisão por zero) como "DBL_EPSILON", que é o valor padrão representando o menor número positivo possível no tipo "double".
3. Se todas as etapas forem realizadas com sucesso, o método retorna "true", indicando que a inicialização do algoritmo foi bem-sucedida.
O método "Init" é uma parte importante da preparação do algoritmo para execução, pois define os principais parâmetros que serão utilizados no processo de otimização. A chamada a este método resulta na redefinição de todos os parâmetros e variáveis para seu estado inicial.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_AOA::Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0) // Количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Инициализация стандартных параметров //---------------------------------------------------------------------------- epochs = epochsP; // Установка общего количества эпох epochNow = 0; // Инициализация текущей эпохи ϵ = DBL_EPSILON; // Установка значения ϵ return true; // Возвращаем true при успешной инициализации } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" é responsável pelo deslocamento das partículas no espaço de soluções dentro do algoritmo AOA. Ele implementa a lógica principal de atualização das posições das partículas com base no estado atual e nos parâmetros do algoritmo. A lógica de funcionamento do método:
1. Incrementa o valor de "epochNow", indicando o início de uma nova época de otimização.
2. Posicionamento aleatório inicial: caso ainda não tenha sido realizada a atualização (revisão), são geradas posições aleatórias para cada partícula dentro dos intervalos definidos por "rangeMin" e "rangeMax". Cada posição é então convertida em valor discreto usando o método "SeInDiSp" com o passo especificado.
3. MoAc e MoPr — são calculados com base na época atual e nos parâmetros definidos. Esses valores determinam as probabilidades utilizadas para atualizar as posições das partículas.
4. Fase de diversificação. Para cada partícula e para cada coordenada, a posição é atualizada com base em valores aleatórios e nos parâmetros calculados. As posições podem ser atualizadas utilizando diferentes operadores (divisão e multiplicação), bem como condições probabilísticas.
5. Após a atualização, a posição também é convertida em valor discreto por meio do método "SeInDiSp".
//—————————————————————————————————————————————————————————————————————————————— // Метод перемещения частиц void C_AO_AOA::Moving () { epochNow++; // Увеличиваем номер текущей эпохи // Начальное случайное позиционирование if (!revision) // Если еще не было ревизии { for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Генерация случайной позиции a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } } revision = true; // Установка флага ревизии return; // Выход из метода } //---------------------------------------------------------------------------- double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Вычисление значения MoAc double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ)); // Вычисление значения MoPr double best = 0.0; // Переменная для хранения лучшего значения // Фаза исследования с использованием операторов Деления (D) и Умножения (M) for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { double rand1 = u.RNDprobab (); // Генерация случайного значения double rand2 = u.RNDprobab (); // Генерация случайного значения double rand3 = u.RNDprobab (); // Генерация случайного значения best = cB [c]; // Сохранение текущего лучшего значения if (rand1 < MoAc) // Если случайное значение меньше MoAc { if (rand2 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } } else // Если случайное значение больше или равно MoAc { if (rand3 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" na classe "C_AO_AOA" atualiza a informação sobre a melhor partícula da população. Ele percorre todas as partículas, compara seus valores de função com o valor atual considerado como o melhor e, se encontrar um valor superior, atualiza esse valor e armazena o índice correspondente. Em seguida, copia as coordenadas da melhor partícula para o array "cB".
//—————————————————————————————————————————————————————————————————————————————— void C_AO_AOA::Revision () { int ind = -1; // Индекс для хранения лучшей частицы for (int i = 0; i < popSize; i++) // Для каждой частицы { if (a [i].f > fB) // Если значение функции лучше, чем текущее лучшее { fB = a [i].f; // Обновление лучшего значения функции ind = i; // Сохранение индекса лучшей частицы } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшей частицы } //——————————————————————————————————————————————————————————————————————————————
O método "SeInDiSp" da classe "C_AO_Utilities" limita o valor de entrada "In" ao intervalo [InMin, InMax] com o passo especificado "Step".
1. Se "In" for menor ou igual a "InMin", retorna "InMin".
2. Se "In" for maior ou igual a "InMax", retorna "InMax".
3. Se "Step" for igual a 0, retorna o valor original "In".
4. Caso contrário, arredonda o valor de (In − InMin) ÷ Step e retorna o valor ajustado dentro do intervalo, considerando o passo.
double C_AO_Utilities :: SeInDiSp (double In, double InMin, double InMax, double Step) { if (In <= InMin) return (InMin); if (In >= InMax) return (InMax); if (Step == 0.0) return (In); else return (InMin + Step * (double)MathRound ((In - InMin) / Step)); }
Resultados dos testes
O algoritmo AOA é bastante simples, então vejamos seu desempenho em tarefas de teste.
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3914957505847635
25 Hilly's; Func runs: 10000; result: 0.27733670012505607
500 Hilly's; Func runs: 10000; result: 0.2514517003089684
=============================
5 Forest's; Func runs: 10000; result: 0.23495704012464264
25 Forest's; Func runs: 10000; result: 0.1853447250852242
500 Forest's; Func runs: 10000; result: 0.15382470751079919
=============================
5 Megacity's; Func runs: 10000; result: 0.19846153846153847
25 Megacity's; Func runs: 10000; result: 0.11815384615384619
500 Megacity's; Func runs: 10000; result: 0.09475384615384692
=============================
All score: 1.90578 (21.18%)
Segundo os resultados do teste, o algoritmo alcança apenas 21,18% do total de 100% possível. Um resultado muito fraco, infelizmente inferior até mesmo ao último da tabela de classificação atual. Vamos tentar modificar a lógica do algoritmo para obter resultados melhores. Faremos as mudanças em etapas e monitoraremos os resultados.
A lógica do algoritmo AOA original prevê uma busca estocástica baseada exclusivamente no caráter probabilístico da escolha entre os quatro operadores matemáticos. Vamos adicionar ao coeficiente de deslocamento μ um elemento de aleatoriedade, multiplicando-o por um número aleatório entre 0 e 1.
// Фаза исследования с использованием операторов Деления (D) и Умножения (M) for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { double rand1 = u.RNDprobab (); // Генерация случайного значения double rand2 = u.RNDprobab (); // Генерация случайного значения double rand3 = u.RNDprobab (); // Генерация случайного значения best = cB [c]; // Сохранение текущего лучшего значения μ *= u.RNDfromCI (0, 1); // Случайное изменение параметра μ if (rand1 < MoAc) // Если случайное значение меньше MoAc { if (rand2 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } } else // Если случайное значение больше или равно MoAc { if (rand3 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ + rangeMin [c]); // Обновление позиции частицы } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } }
Vamos testar o algoritmo com os mesmos parâmetros:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.3595591180258857
25 Hilly's; Func runs: 10000; result: 0.2804913285516192
500 Hilly's; Func runs: 10000; result: 0.25204298245610646
=============================
5 Forest's; Func runs: 10000; result: 0.24115834887873383
25 Forest's; Func runs: 10000; result: 0.18034196700384764
500 Forest's; Func runs: 10000; result: 0.15441446106797124
=============================
5 Megacity's; Func runs: 10000; result: 0.18307692307692305
25 Megacity's; Func runs: 10000; result: 0.12400000000000003
500 Megacity's; Func runs: 10000; result: 0.09470769230769309
=============================
All score: 1.86979 (20.78%)
Infelizmente, o resultado foi ainda pior. É necessário tomar medidas adicionais. No entanto, o simples fato de adicionar aleatoriedade a uma expressão determinística deve, sem dúvida, melhorar a variabilidade da estratégia de busca. Observemos atentamente as fórmulas dos operadores matemáticos — em cada uma delas há o termo "rangeMin[c]". Na prática, as expressões desses operadores são sempre centradas em torno do limite mínimo dos parâmetros otimizados. Isso não parece ter uma lógica evidente, então removeremos esse elemento de todas as fórmulas.
// Фаза исследования с использованием операторов Деления (D) и Умножения (M) for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { double rand1 = u.RNDprobab (); // Генерация случайного значения double rand2 = u.RNDprobab (); // Генерация случайного значения double rand3 = u.RNDprobab (); // Генерация случайного значения best = cB [c]; // Сохранение текущего лучшего значения μ *= u.RNDfromCI (0, 1); // Изменение параметра μ if (rand1 < MoAc) // Если случайное значение меньше MoAc { if (rand2 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Обновление позиции частицы } } else // Если случайное значение больше или равно MoAc { if (rand3 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Обновление позиции частицы } else { a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ);// + rangeMin [c]); // Обновление позиции частицы } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } }
Testando. Abaixo estão os resultados obtidos:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.36094646986361645
25 Hilly's; Func runs: 10000; result: 0.28294095623218063
500 Hilly's; Func runs: 10000; result: 0.2524581968477915
=============================
5 Forest's; Func runs: 10000; result: 0.2463208325927641
25 Forest's; Func runs: 10000; result: 0.1772140022690996
500 Forest's; Func runs: 10000; result: 0.15367993432040622
=============================
5 Megacity's; Func runs: 10000; result: 0.1923076923076923
25 Megacity's; Func runs: 10000; result: 0.11938461538461542
500 Megacity's; Func runs: 10000; result: 0.09433846153846229
=============================
All score: 1.87959 (20.88%)
As modificações realizadas não levaram à melhoria do desempenho, o que é bastante estranho, considerando que já aplicamos mudanças significativas na estratégia de busca. Isso pode indicar que a própria estratégia apresenta deficiências e que a remoção de componentes isolados não tem impacto significativo nos resultados.
Na estratégia de busca há o componente MoA, que cresce linearmente a cada iteração (ver figura 1). Vamos tentar utilizar esse componente como critério probabilístico para escolher uma das coordenadas da melhor solução e copiá-la para a solução em trabalho atual. Isso deve adicionar propriedades combinatórias à estratégia de busca, por meio da troca de informações com a melhor solução da população (na versão original dos autores, não há troca de informações entre os agentes).
// Фаза исследования с использованием операторов Деления (D) и Умножения (M) for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { double rand1 = u.RNDprobab (); // Генерация случайного значения double rand2 = u.RNDprobab (); // Генерация случайного значения double rand3 = u.RNDprobab (); // Генерация случайного значения best = cB [c]; // Сохранение текущего лучшего значения μ *= u.RNDfromCI (0, 1); // Изменение параметра μ if (rand1 < MoAc) // Если случайное значение меньше MoAc { if (rand2 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best / (MoPr + ϵ) * ((rangeMax [c] - rangeMin [c]) * μ); // Обновление позиции частицы } else { a [i].c [c] = best * (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ); // Обновление позиции частицы } } else // Если случайное значение больше или равно MoAc { if (rand3 > 0.5) // Если случайное значение больше 0.5 { a [i].c [c] = best - (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ); // Обновление позиции частицы } else { a [i].c [c] = best + (MoPr) * ((rangeMax [c] - rangeMin [c]) * μ); // Обновление позиции частицы } } if (u.RNDbool () < MoAc) a [i].c [c] = cB [c]; // Установка на лучшее значение a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } }
Resultados obtidos após a introdução da lógica de troca de informações por meio da melhor solução:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.360814744695913
25 Hilly's; Func runs: 10000; result: 0.28724958448168375
500 Hilly's; Func runs: 10000; result: 0.2523432997811412
=============================
5 Forest's; Func runs: 10000; result: 0.26319762212870146
25 Forest's; Func runs: 10000; result: 0.1796822846691542
500 Forest's; Func runs: 10000; result: 0.1546335398592898
=============================
5 Megacity's; Func runs: 10000; result: 0.18
25 Megacity's; Func runs: 10000; result: 0.12153846153846157
500 Megacity's; Func runs: 10000; result: 0.09373846153846228
=============================
All score: 1.89320 (21.04%)
Observamos melhorias no desempenho, embora ainda dentro da margem de variação dos próprios resultados. Agora vamos adicionar, nessa mesma parte do código, uma probabilidade de gerar um valor aleatório para a coordenada dentro de todo o intervalo permitido dos parâmetros otimizados, que diminui de forma não linear de acordo com a fórmula de MoP.
// Вероятностное обновление позиции частицы if (u.RNDbool () < MoAc) a [i].c [c] = cB [c]; // Установка на лучшее значение else if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Генерация новой случайной позиции
Analisemos os próximos resultados:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.8354927331645667
25 Hilly's; Func runs: 10000; result: 0.3963221867834875
500 Hilly's; Func runs: 10000; result: 0.2526544322311671
=============================
5 Forest's; Func runs: 10000; result: 0.7689954585427405
25 Forest's; Func runs: 10000; result: 0.3144560745800252
500 Forest's; Func runs: 10000; result: 0.15495875390289315
=============================
5 Megacity's; Func runs: 10000; result: 0.6076923076923076
25 Megacity's; Func runs: 10000; result: 0.24646153846153843
500 Megacity's; Func runs: 10000; result: 0.09816923076923163
=============================
All score: 3.67520 (40.84%)
Surpreendentemente, o desempenho aumentou drasticamente! Isso indica que estamos seguindo na direção certa. Vale destacar o que foi adicionado à lógica do AOA: no início da otimização, na primeira época, a probabilidade de copiar coordenadas da melhor solução global para a solução atual é mínima. Isso faz sentido, já que no estágio inicial da otimização a estratégia está apenas começando a explorar o espaço de busca. Ao mesmo tempo, a probabilidade de gerar soluções aleatórias dentro de todo o espaço de busca é máxima na primeira iteração. Ao longo das épocas, essas probabilidades se alteram: a probabilidade de copiar coordenadas da solução global aumenta, enquanto a de gerar soluções aleatórias diminui (ver figura 1).
Como o desempenho melhorou após as alterações que implementei — e como já havia sido observado anteriormente que mudanças na lógica original dos autores não traziam melhorias significativas — faz sentido remover completamente todos os operadores aritméticos. Vamos testar o algoritmo resultante nas tarefas de teste:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.9|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8751771961221438
25 Hilly's; Func runs: 10000; result: 0.4645369071659114
500 Hilly's; Func runs: 10000; result: 0.27170038319811357
=============================
5 Forest's; Func runs: 10000; result: 0.8369443889312367
25 Forest's; Func runs: 10000; result: 0.36483865328371257
500 Forest's; Func runs: 10000; result: 0.17097532914778202
=============================
5 Megacity's; Func runs: 10000; result: 0.7046153846153846
25 Megacity's; Func runs: 10000; result: 0.28892307692307695
500 Megacity's; Func runs: 10000; result: 0.10847692307692398
=============================
All score: 4.08619 (45.40%)
Como se pode ver, a performance aumentou quase 5% a mais, o que confirma novamente a correção do meu raciocínio. Obtivemos resultados interessantes usando os parâmetros padrão, no entanto, as mudanças na lógica foram tão profundas que agora é necessário ajustar os parâmetros externos do algoritmo para obter o melhor desempenho. Um bônus adicional do ganho de desempenho foi:
- aceleração significativa na execução, já que eliminamos gerações desnecessárias de números aleatórios
- redução de um parâmetro externo do algoritmo
Vejamos os resultados finais do algoritmo resultante:
AOA|Arithmetic Optimization Algorithm|50.0|0.1|0.5|10.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9152036654779877
25 Hilly's; Func runs: 10000; result: 0.46975580956945456
500 Hilly's; Func runs: 10000; result: 0.27088799720164297
=============================
5 Forest's; Func runs: 10000; result: 0.8967497776673259
25 Forest's; Func runs: 10000; result: 0.3740125122006007
500 Forest's; Func runs: 10000; result: 0.16983896751516864
=============================
5 Megacity's; Func runs: 10000; result: 0.6953846153846155
25 Megacity's; Func runs: 10000; result: 0.2803076923076923
500 Megacity's; Func runs: 10000; result: 0.10852307692307792
=============================
All score: 4.18066 (46.45%)
O resultado obtido já merece um lugar na tabela de classificação, e a versão final da estratégia de busca perdeu completamente os elementos da lógica original do algoritmo dos autores. Por isso, decidi dar a esse novo algoritmo um novo nome — Simple Optimization Algorithm, ou SAO (Algoritmo de Otimização Simples). Vamos conferir o código final completo do algoritmo SAO.
#include "#C_AO.mqh" //—————————————————————————————————————————————————————————————————————————————— class C_AO_SOA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_SOA () { } C_AO_SOA () { ao_name = "SOA"; ao_desc = "Simple Optimization Algorithm"; ao_link = "https://www.mql5.com/ru/articles/16364"; popSize = 50; // Размер популяции minT = 0.1; // Минимальное значение T maxT = 0.9; // Максимальное значение T θ = 10; // Параметр θ ArrayResize (params, 4); // Изменение размера массива параметров // Инициализация параметров params [0].name = "popSize"; params [0].val = popSize; params [1].name = "minT"; params [1].val = minT; params [2].name = "maxT"; params [2].val = maxT; params [3].name = "θ"; params [3].val = θ; } void SetParams () // Метод для установки параметров { popSize = (int)params [0].val; // Установка размера популяции minT = params [1].val; // Установка минимального T maxT = params [2].val; // Установка максимального T θ = params [3].val; // Установка параметра θ } bool Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0); // Количество эпох void Moving (); // Метод перемещения частиц void Revision (); // Метод ревизии //---------------------------------------------------------------------------- double minT; // Минимальное значение T double maxT; // Максимальное значение T double θ; // Параметр θ private: //------------------------------------------------------------------- int epochs; // Общее количество эпох int epochNow; // Текущая эпоха double ϵ; // Параметр для предотвращения деления на ноль }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— bool C_AO_SOA::Init (const double &rangeMinP [], // Минимальный диапазон поиска const double &rangeMaxP [], // Максимальный диапазон поиска const double &rangeStepP [], // Шаг поиска const int epochsP = 0) // Количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; // Инициализация стандартных параметров //---------------------------------------------------------------------------- epochs = epochsP; // Установка общего количества эпох epochNow = 0; // Инициализация текущей эпохи ϵ = DBL_EPSILON; // Установка значения ϵ return true; // Возвращаем true при успешной инициализации } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Метод перемещения частиц void C_AO_SOA::Moving () { epochNow++; // Увеличиваем номер текущей эпохи // Начальное случайное позиционирование if (!revision) // Если еще не было ревизии { for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Генерация случайной позиции a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } } revision = true; // Установка флага ревизии return; // Выход из метода } //---------------------------------------------------------------------------- double MoAc = minT + epochNow * ((maxT - minT) / epochs); // Вычисление значения MoAc double MoPr = 1.0 - pow (epochNow / epochs, (1.0 / θ)); // Вычисление значения MoPr double best = 0.0; // Переменная для хранения лучшего значения // Фаза исследования с использованием операторов Деления (D) и Умножения (M) for (int i = 0; i < popSize; i++) // Для каждой частицы { for (int c = 0; c < coords; c++) // Для каждой координаты { // Вероятностное обновление позиции частицы if (u.RNDbool () < MoAc) a [i].c [c] = cB [c]; // Установка на лучшее значение else if (u.RNDbool () < MoPr) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Генерация новой случайной позиции a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); // Приведение к дискретным значениям } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void C_AO_SOA::Revision () { int ind = -1; // Индекс для хранения лучшей частицы for (int i = 0; i < popSize; i++) // Для каждой частицы { if (a [i].f > fB) // Если значение функции лучше, чем текущее лучшее { fB = a [i].f; // Обновление лучшего значения функции ind = i; // Сохранение индекса лучшей частицы } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшей частицы } //——————————————————————————————————————————————————————————————————————————————
Obtivemos um dos algoritmos de otimização com código mais compacto dentre todos os que analisamos até agora. Apenas o código do algoritmo RW (RandomWalk), que será abordado em um dos próximos artigos, é ainda mais curto.
A visualização do funcionamento das estratégias de busca no espaço de soluções fala mais do que qualquer explicação. Reuni os três testes (Hilly, Forest e Megacity) para o algoritmo AOA em uma única animação, já que praticamente não há diferença perceptível no comportamento do algoritmo em diferentes tipos de tarefas. Abaixo são mostradas visualizações individuais do funcionamento do SOA para cada uma das três funções de teste.
É possível destacar o desempenho do novo algoritmo SOA em tarefas de baixa dimensionalidade — pequena dispersão nos resultados e qualidade aceitável em intervalos razoáveis.
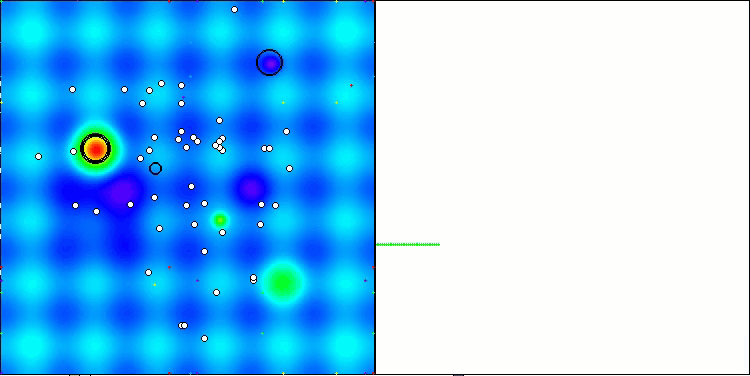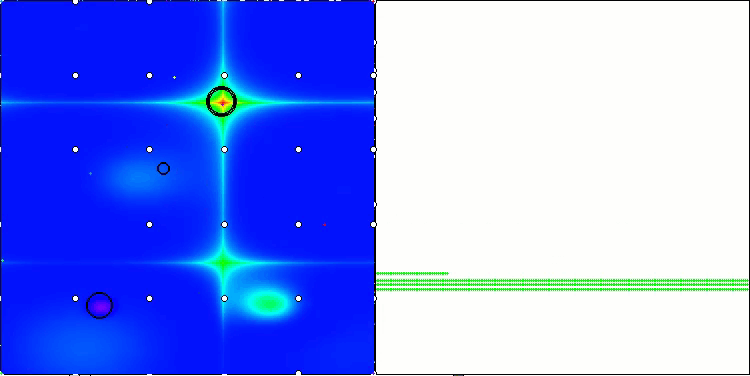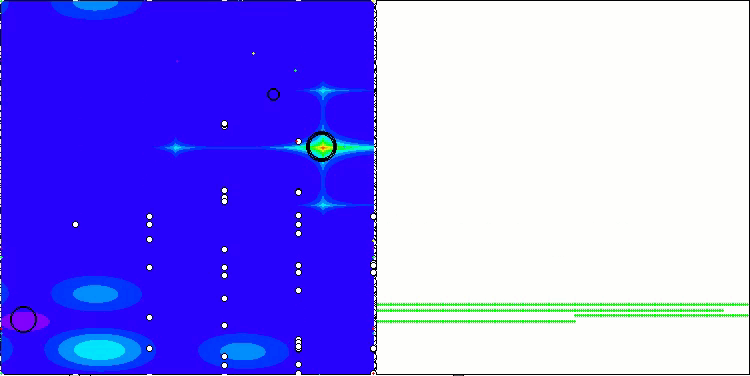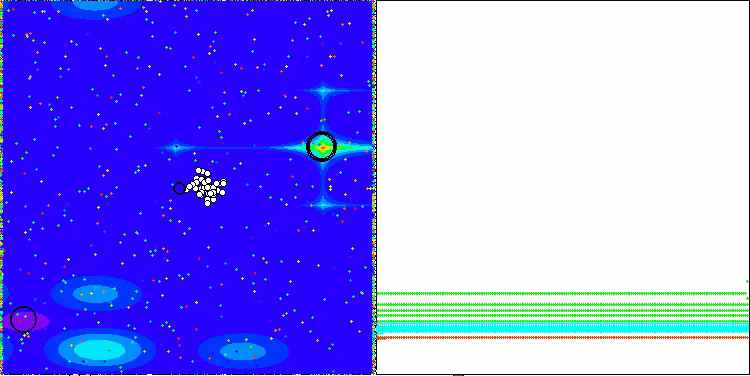
AOA nas funções de teste Hilly, Forest, Megacity
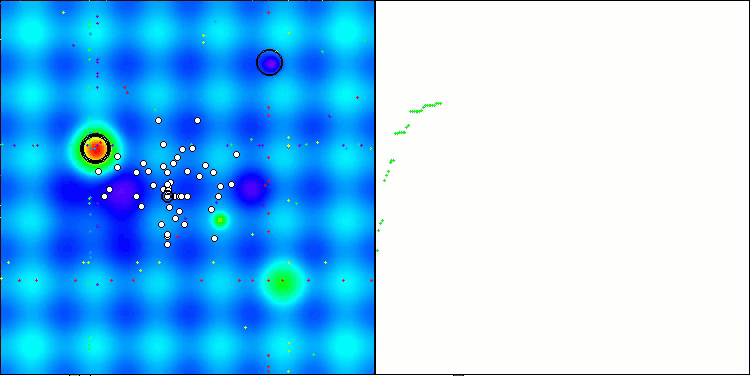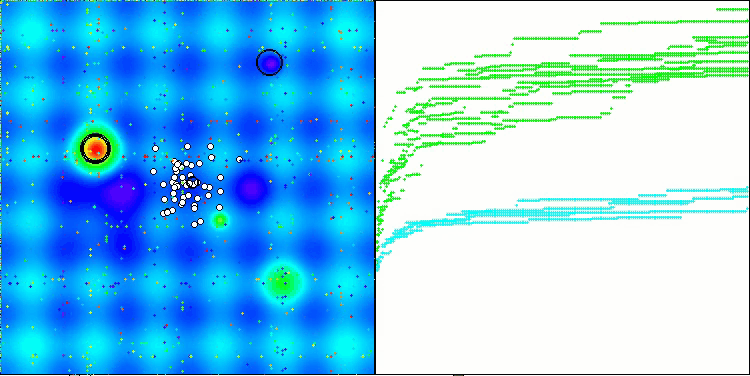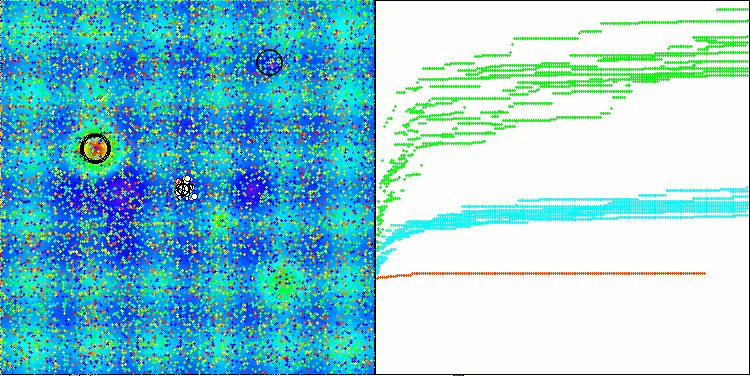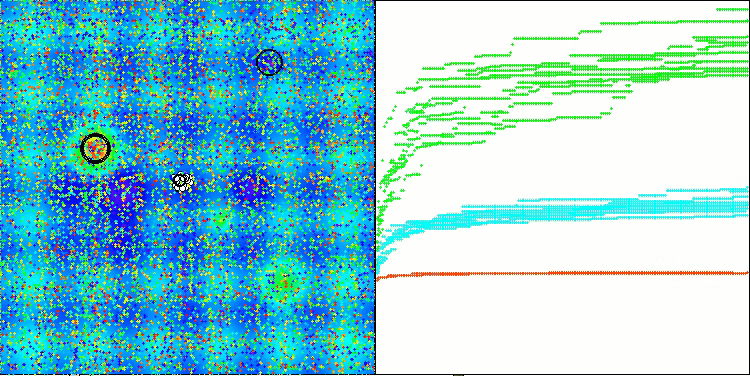
SOA na função de teste Hilly
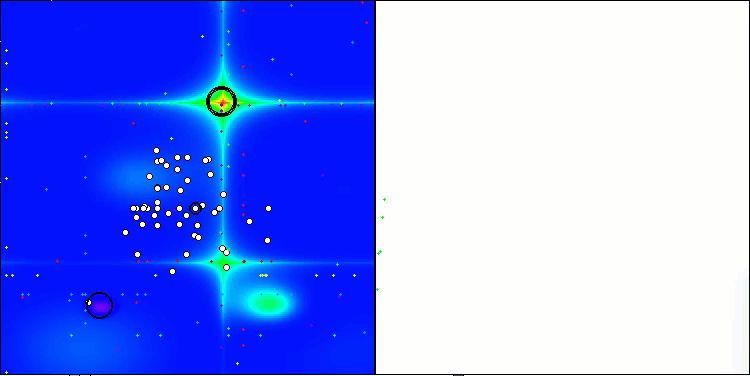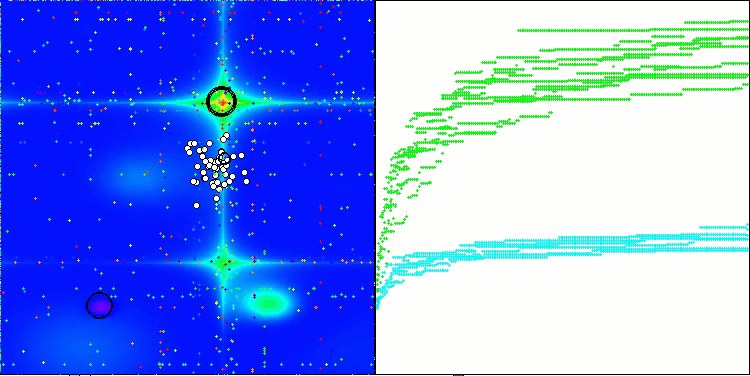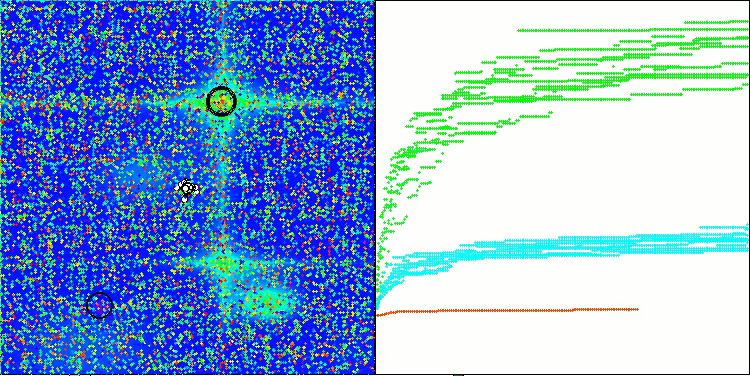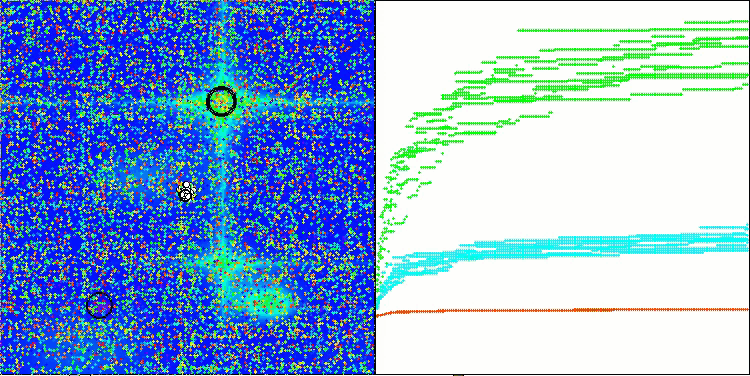
SOA na função de teste Forest
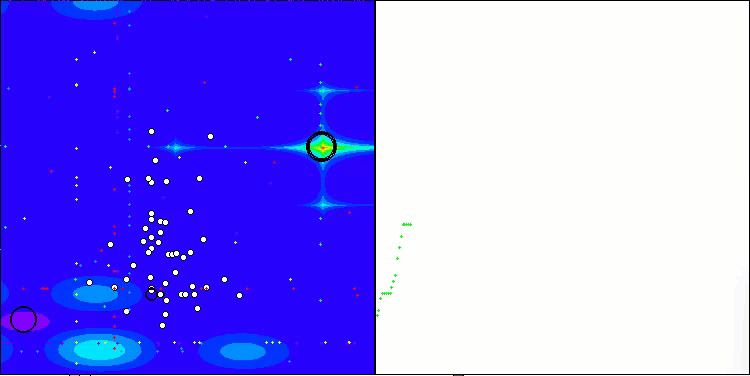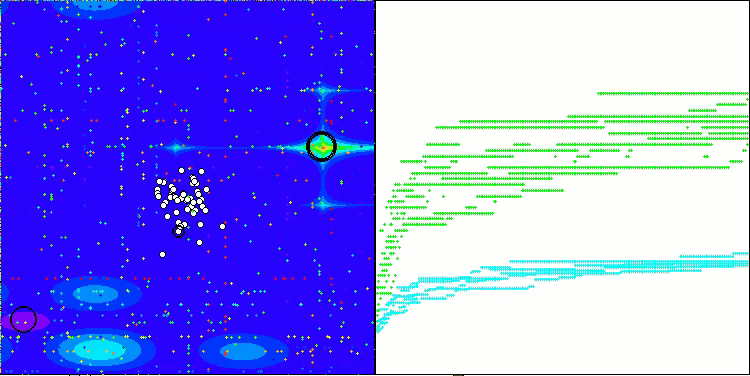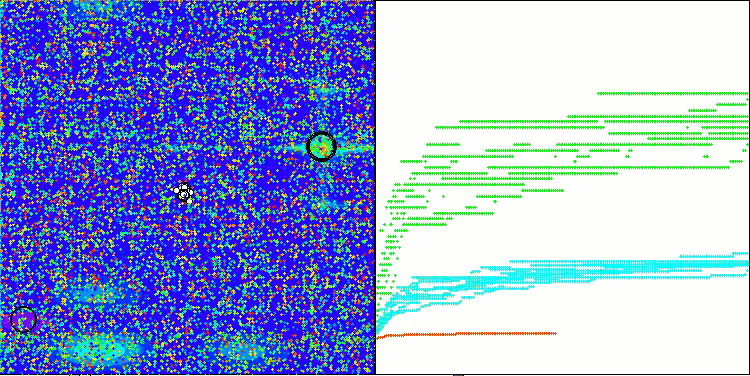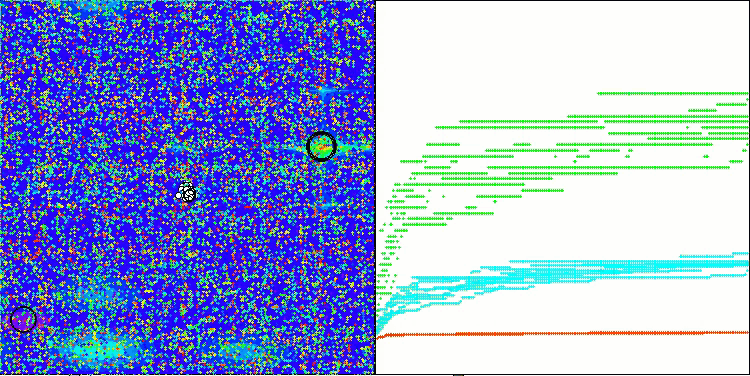
SOA na função de teste Megacity
Como resultado dos testes, o algoritmo original AOA não entrou na tabela de classificação, já que sua pontuação ficou abaixo da 45ª posição. Por outro lado, o novo algoritmo “Simple Optimization Algorithm” (SOA) entrou no ranking e ficou em 29º lugar.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 14 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 15 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 16 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 17 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 18 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 20 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 21 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 22 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 23 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 24 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 25 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 27 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 29 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 30 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 31 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 32 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 33 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 34 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 35 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 36 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 37 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 38 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 39 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 40 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 41 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 42 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 43 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 44 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 45 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
Considerações finais
Analisamos detalhadamente o Algoritmo de Otimização Aritmética, cuja implementação se mostrou realmente simples. No entanto, como às vezes acontece, simplicidade nem sempre garante resultados excelentes. O verdadeiro segredo do sucesso é a super simplicidade! Claro que isso é uma brincadeira. Os principais problemas do AOA estão na ausência de interação e troca de informações entre os membros da população, o que leva à completa falta de propriedades combinatórias nessa estratégia de busca.
Outro ponto fraco do algoritmo está na ausência de variabilidade em seus operadores de busca. Apesar de os operadores serem escolhidos aleatoriamente para cada coordenada, isso não permite que o algoritmo se conecte eficientemente ao relevo multidimensional do espaço de busca. Ainda assim, o algoritmo AOA apresenta abordagens racionais e logicamente fundamentadas, como os elementos MoA e MoP, que variam a cada época. Foram esses elementos que se tornaram a base para a recriação do algoritmo e sua evolução para uma nova estratégia de busca extremamente simples e interessante baseada na abordagem probabilística de copiar informações das melhores soluções da população e gerar soluções aleatórias dentro do espaço de busca.
A cada época, a aleatoriedade nas soluções da população diminui, enquanto aumenta a concentração nas direções bem-sucedidas. Isso pode ser comparado ao processo de construção de uma ponte elegante sobre um rio: nas etapas iniciais, são utilizados diversos materiais e estruturas que, talvez, não sejam adequados para o resultado final. No entanto, à medida que o projeto avança, as melhores soluções se tornam mais evidentes e os elementos desnecessários são descartados. Como resultado, a ponte torna-se cada vez mais harmônica e resistente, conectando as margens com elegância e solidez.
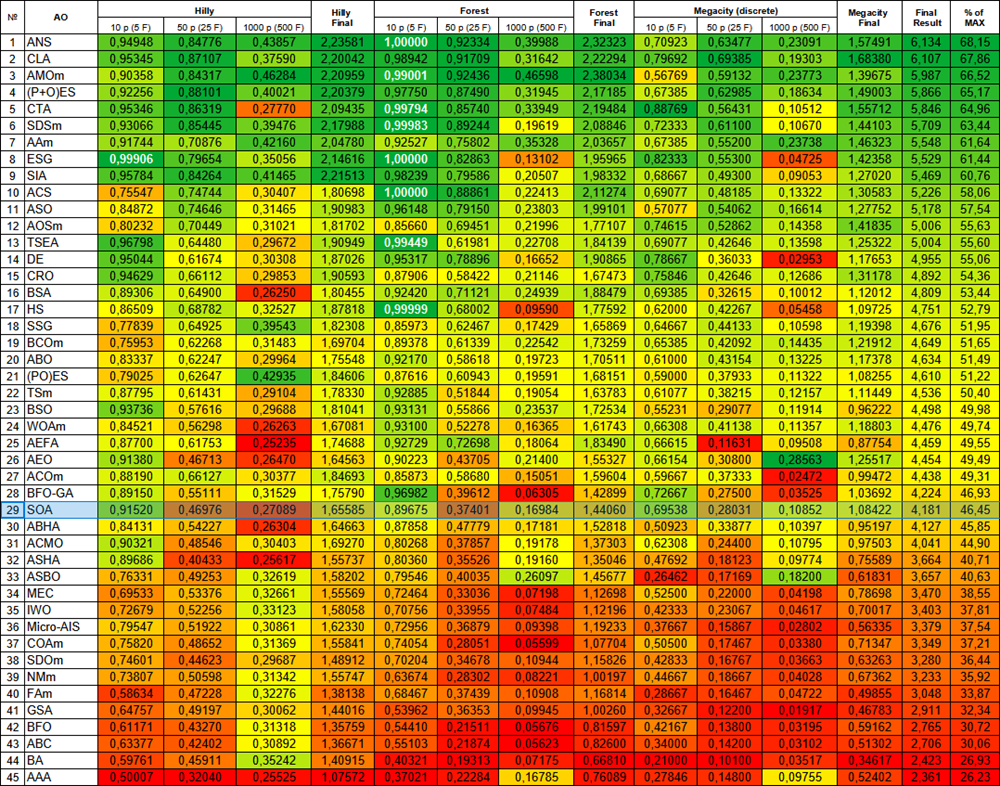
Figura 2. Gradação de cores dos algoritmos conforme os respectivos testes. A cor branca destaca resultados maiores ou iguais a 0,99
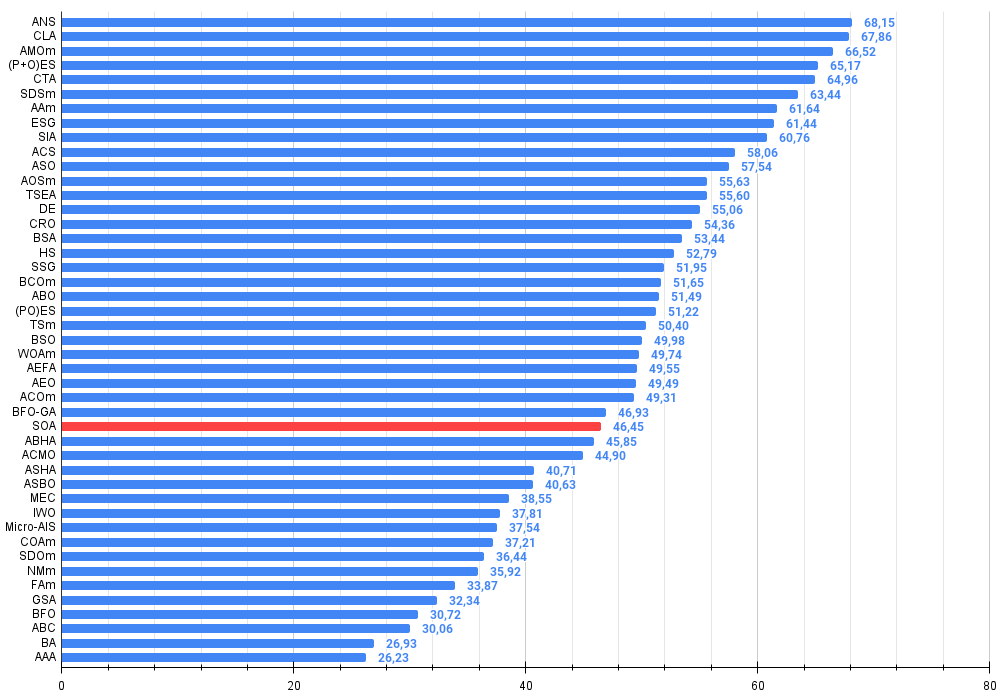
Figura 3. Histograma dos resultados de teste dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo há um script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo SOA:
Vantagens:
- Poucos parâmetros externos.
- Bons resultados em tarefas de baixa dimensionalidade, especialmente nas discretas.
- Rápido.
- Baixa variação nos resultados em tarefas de baixa dimensionalidade.
- Implementação extremamente simples.
Desvantagens:
- Baixa escalabilidade.
Está anexado ao artigo um arquivo compactado contendo as versões mais recentes dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta da descrição dos algoritmos canônicos, já que muitos deles foram modificados para aprimorar suas capacidades de busca. As conclusões e observações apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluível | Classe-pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluível | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluível | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluível | Biblioteca de funções do banco de testes |
| 5 | Utilities.mqh | Arquivo incluível | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluível | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Banco de testes unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso dos algoritmos populacionais de otimização sem visualização |
| 9 | AO_AOA_ArithmeticOptimizationAlgorithm.mqh | Arquivo incluível | Classe do algoritmo AOA |
| 10 | AO_SOA_SimpleOptimizationAlgorithm.mqh | Arquivo incluível | Classe do algoritmo SOA |
| 11 | Test_AO_AOA.mq5 | Script | Banco de testes para o AOA |
| 12 | Test_AO_SOA.mq5 | Script | Banco de testes para o SOA |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16364
 Redes neurais em trading: Transformer parâmetro-eficiente com atenção segmentada (PSformer)
Redes neurais em trading: Transformer parâmetro-eficiente com atenção segmentada (PSformer)
 Recursos do Assistente MQL5 que você precisa conhecer (Parte 40): Parabolic SAR
Recursos do Assistente MQL5 que você precisa conhecer (Parte 40): Parabolic SAR
 Redes neurais em trading: Transformer eficiente em parâmetros com atenção segmentada (Conclusão)
Redes neurais em trading: Transformer eficiente em parâmetros com atenção segmentada (Conclusão)
 Simulação de mercado (Parte 20): Iniciando o SQL (III)
Simulação de mercado (Parte 20): Iniciando o SQL (III)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso