
Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte V): Modelos profundos de Markov
En nuestra discusión anterior sobre las cadenas de Markov, vinculadas aquí, demostramos cómo utilizar una matriz de transición para comprender el comportamiento probabilístico del mercado. Nuestra matriz de transición resumió mucha información para nosotros. No sólo nos orientó sobre cuándo comprar y vender, sino que también nos informó si nuestro mercado tenía tendencias fuertes o si estaba mayoritariamente revirtiendo a la media. En la discusión de hoy, cambiaremos nuestra definición del estado del sistema de los promedios móviles que usamos en nuestra primera discusión al Indicador de Fuerza Relativa (RSI).
Cuando a la mayoría de las personas se les enseña cómo operar utilizando el RSI, se les dice que compren cuando el RSI llegue a 30 y vendan cuando llegue a 70. Algunos miembros de la comunidad pueden preguntarse si esta es la mejor decisión a tomar en todos los mercados. Todos sabemos que no es posible operar en todos los mercados de la misma manera. Este artículo le demostrará cómo puede construir sus propias cadenas de Markov para aprender algorítmicamente reglas comerciales óptimas. No sólo eso, sino que las reglas que aprenderemos se ajustarán dinámicamente a los datos que recopile del mercado en el que desea operar.
Descripción general de la estrategia comercial
Los analistas técnicos utilizan ampliamente el RSI para identificar niveles de precios extremos. Normalmente los precios del mercado tienden a volver a sus promedios. Por lo tanto, siempre que los analistas de precios encuentran un valor rondando niveles RSI extremos, normalmente apostarán contra la tendencia dominante. Esta estrategia ha sido ligeramente modificada en muchas versiones diferentes, todas ellas derivadas de una misma fuente. La deficiencia de esta estrategia es que lo que puede considerarse un nivel de RSI fuerte en un mercado, no es necesariamente un nivel de RSI fuerte para todos los mercados.
Para ilustrar este punto, la Figura 1 a continuación nos muestra cómo evoluciona la desviación estándar del valor RSI en 2 mercados diferentes. La línea azul representa la desviación estándar promedio del RSI en el mercado XPDUSD, mientras que la línea naranja representa el mercado NZDJPY. Es ampliamente conocido por todos los traders experimentados que el mercado de metales preciosos es significativamente volátil. Por lo tanto, podemos ver una clara disparidad entre los cambios en los niveles de RSI entre los dos mercados. Lo que puede considerarse una lectura alta para el RSI en un par de divisas, como el par NZDUSD, puede considerarse ruido de mercado normal cuando se negocia un instrumento más volátil, como el XPDUSD.
Pronto se hace evidente que cada mercado podría tener su propio nivel único de interés en el indicador RSI. En otras palabras, cuando utilizamos el indicador RSI, el nivel óptimo para ingresar a una operación depende del símbolo que se esté negociando. Por lo tanto, ¿cómo podemos aprender algorítmicamente en qué nivel de RSI debemos comprar o vender? Podemos emplear nuestra matriz de transición para responder esta pregunta para cualquier símbolo que tengamos en mente.
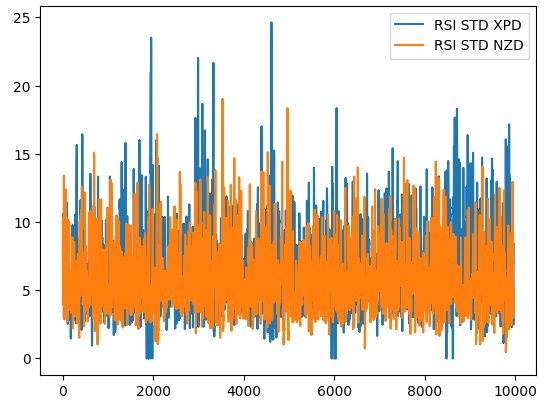
Figura 1: La volatilidad móvil del indicador RSI en el mercado XPDUSD en azul y el mercado NZDUSD en naranja
Descripción general de la metodología
Para aprender nuestra estrategia a partir de los datos que tenemos, primero recopilamos 300.000 filas de datos M1 utilizando la biblioteca MetaTrader 5 para Python. Etiquetamos los datos y luego los dividimos en divisiones de entrenamiento y prueba. En el conjunto de entrenamiento, agrupamos las lecturas del RSI en 10 intervalos, de 0 a 10, de 11 a 20, linealmente hasta 91 a 100. Registramos el comportamiento futuro del precio al pasar por cada grupo del RSI. Los datos de entrenamiento mostraron que los niveles de precios tenían la mayor tendencia a apreciarse siempre que el precio pasaba por la zona 41-50 del RSI y la mayor tendencia a depreciarse por la zona 61-70.
Utilizamos esta matriz de transición estimada para construir un modelo codicioso que siempre selecciona el resultado más probable de las distribuciones anteriores. Nuestro modelo simple obtuvo una precisión del 52% en el conjunto de pruebas. Otra ventaja de este enfoque es su interoperabilidad, podemos entender fácilmente cómo nuestro modelo está tomando sus decisiones. Además, ahora es común que los modelos de IA que se utilizan en industrias importantes sean explicables, y puede estar seguro de que esta familia de modelos probabilísticos no le generará problemas de cumplimiento.
Siguiendo adelante, nuestro interés no estaba enteramente en la precisión del modelo. Más bien, nos centramos en los niveles de precisión individuales de las 10 zonas que identificamos en nuestro conjunto de entrenamiento. Ninguna de las dos zonas, que tenían las distribuciones más altas en nuestro conjunto de entrenamiento, resultó confiable en el conjunto de validación. En el conjunto de validación de los datos, obtuvimos la mayor precisión cuando compramos en el rango 11-20 y vendimos en el rango 71-80. Tuvimos niveles de precisión de 51,4% y 75,8% en las respectivas zonas. Seleccionamos estas zonas como nuestras zonas óptimas para abrir posiciones de compra y venta en el par NZDJPY.
Finalmente, nos propusimos construir un Asesor Experto MQL5, que implementó los resultados de nuestro análisis en Python. Además, implementamos 2 formas de cerrar posiciones en nuestra aplicación. Le dimos al usuario la decisión de cerrar posiciones cuando el RSI cruce a una zona que disminuirá nuestras posiciones abiertas, o alternativamente, podrían cerrar posiciones cuando el precio cruce la media móvil.
Obtención y limpieza de datos
Comencemos, importemos las bibliotecas que necesitamos.
#Let's get started import MetaTrader5 as mt5 import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt import pandas_ta as ta
Compruebe si se puede acceder la terminal.
mt5.initialize()
Defina algunas variables globales.
#Fetch market data SYMBOL = "NZDJPY" TIMEFRAME = mt5.TIMEFRAME_M1
Copiemos los datos de nuestro terminal.
data = pd.DataFrame(mt5.copy_rates_from_pos(SYMBOL,TIMEFRAME,0,300000))
Convierte el formato de tiempo de segundos.
data["time"] = pd.to_datetime(data["time"],unit='s')
Calcular el RSI.
data.ta.rsi(length=20,append=True) Define hasta qué punto en el futuro debemos pronosticar.
#Define the look ahead look_ahead = 20
Etiqueta los datos.
#Label the data data["Target"] = np.nan data.loc[data["close"] > data["close"].shift(-20),"Target"] = -1 data.loc[data["close"] < data["close"].shift(-20),"Target"] = 1
Eliminar todas las filas faltantes de los datos.
data.dropna(inplace=True) data.reset_index(inplace=True,drop=True)
Cree un vector para representar los 10 grupos de valores RSI.
#Create a dataframe rsi_matrix = pd.DataFrame(columns=["0-10","11-20","21-30","31-40","41-50","51-60","61-70","71-80","81-90","91-100"],index=[0])
Así es como se ven nuestros datos hasta ahora.
Datos
Figura 2: Algunas de las columnas de nuestro marco de datos.
Inicialice la matriz RSI a todo 0.
#Initialize the rsi matrix to 0 for i in np.arange(0,9): rsi_matrix.iloc[0,i] = 0
Particionar los datos.
#Split the data into train and test sets train = data.loc[:(data.shape[0]//2),:] test = data.loc[(data.shape[0]//2):,:]
Ahora revisaremos el conjunto de datos de entrenamiento y observaremos cada lectura de RSI y el cambio futuro correspondiente en los niveles de precios. Si la lectura del RSI fue 11 y los niveles de precios se apreciaron 20 pasos en el futuro, incrementaremos la columna 11-20 correspondiente en nuestra matriz RSI en uno. Además, cada vez que los niveles de precios caigan, penalizaremos la columna y la decrementaremos en uno. Intuitivamente, comprendemos rápidamente que al final, cualquier columna con un valor positivo corresponde a un nivel RSI que tuvo una tendencia a preceder niveles de precios crecientes y lo opuesto es cierto para las columnas que tendrán valores negativos.
for i in np.arange(0,train.shape[0]): #Fill in the rsi matrix, what happened in the future when we saw RSI readings below 10? if((train.loc[i,"RSI_20"] <= 10)): rsi_matrix.iloc[0,0] = rsi_matrix.iloc[0,0] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 11 and 20? if((train.loc[i,"RSI_20"] > 10) & (train.loc[i,"RSI_20"] <= 20)): rsi_matrix.iloc[0,1] = rsi_matrix.iloc[0,1] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 21 and 30? if((train.loc[i,"RSI_20"] > 20) & (train.loc[i,"RSI_20"] <= 30)): rsi_matrix.iloc[0,2] = rsi_matrix.iloc[0,2] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 31 and 40? if((train.loc[i,"RSI_20"] > 30) & (train.loc[i,"RSI_20"] <= 40)): rsi_matrix.iloc[0,3] = rsi_matrix.iloc[0,3] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 41 and 50? if((train.loc[i,"RSI_20"] > 40) & (train.loc[i,"RSI_20"] <= 50)): rsi_matrix.iloc[0,4] = rsi_matrix.iloc[0,4] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 51 and 60? if((train.loc[i,"RSI_20"] > 50) & (train.loc[i,"RSI_20"] <= 60)): rsi_matrix.iloc[0,5] = rsi_matrix.iloc[0,5] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 61 and 70? if((train.loc[i,"RSI_20"] > 60) & (train.loc[i,"RSI_20"] <= 70)): rsi_matrix.iloc[0,6] = rsi_matrix.iloc[0,6] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 71 and 80? if((train.loc[i,"RSI_20"] > 70) & (train.loc[i,"RSI_20"] <= 80)): rsi_matrix.iloc[0,7] = rsi_matrix.iloc[0,7] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 81 and 90? if((train.loc[i,"RSI_20"] > 80) & (train.loc[i,"RSI_20"] <= 90)): rsi_matrix.iloc[0,8] = rsi_matrix.iloc[0,8] + train.loc[i,"Target"] #What tends to happen in the future, after seeing RSI readings between 91 and 100? if((train.loc[i,"RSI_20"] > 90) & (train.loc[i,"RSI_20"] <= 100)): rsi_matrix.iloc[0,9] = rsi_matrix.iloc[0,9] + train.loc[i,"Target"]
Esta es la distribución de recuentos en el conjunto de entrenamiento. Hemos llegado a nuestro primer problema, no había observaciones de entrenamiento en la zona 91-100. Por lo tanto, decidí asumir que, dado que todas las zonas vecinas resultaron en niveles de precios en caída, asignaremos a la zona un valor negativo arbitrario.
rsi_matrix
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 4.0 | 47.0 | 221.0 | 1171.0 | 3786.0 | 945.0 | -1159.0 | -35.0 | -3.0 | NaN |
Podemos visualizar esta distribución. Parece que el precio pasa la mayor parte del tiempo en la zona 31-70. Esto corresponde a la parte media del RSI. Como mencionamos anteriormente, el precio parecía ser muy alcista en la región 41-50 y bajista en la región 61-70. Sin embargo, estos parecían ser simplemente artefactos de los datos de entrenamiento porque esta relación no se mantuvo en los datos de validación.
sns.barplot(rsi_matrix)
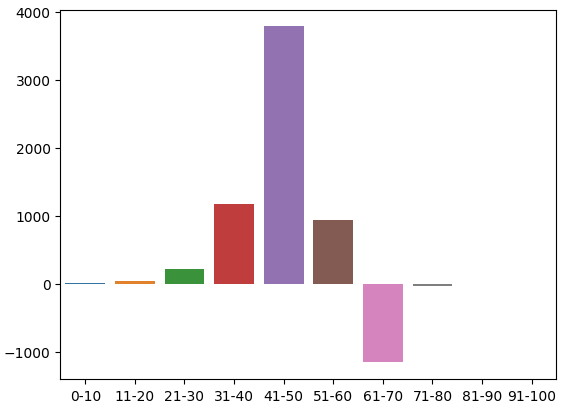
Figura 3: Distribución de los efectos observados de las zonas RSI.
Figura 4: Una representación visual de nuestras transformaciones hasta ahora.
Ahora evaluaremos la precisión de nuestro modelo en los datos de validación. Primero, restablezca el índice de los datos de entrenamiento.
test.reset_index(inplace=True,drop=True)
Crea una columna para las predicciones de nuestro modelo.
test["Predictions"] = np.nan Complete las predicciones de nuestro modelo.
for i in np.arange(0,test.shape[0]): #Fill in the predictions if((test.loc[i,"RSI_20"] <= 10)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 10) & (test.loc[i,"RSI_20"] <= 20)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 20) & (test.loc[i,"RSI_20"] <= 30)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 30) & (test.loc[i,"RSI_20"] <= 40)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 40) & (test.loc[i,"RSI_20"] <= 50)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 50) & (test.loc[i,"RSI_20"] <= 60)): test.loc[i,"Predictions"] = 1 if((test.loc[i,"RSI_20"] > 60) & (test.loc[i,"RSI_20"] <= 70)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 70) & (test.loc[i,"RSI_20"] <= 80)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 80) & (test.loc[i,"RSI_20"] <= 90)): test.loc[i,"Predictions"] = -1 if((test.loc[i,"RSI_20"] > 90) & (test.loc[i,"RSI_20"] <= 100)): test.loc[i,"Predictions"] = -1
Validamos que no tengamos ningún valor nulo.
test.loc[:,"Predictions"].isna().any() Describamos la relación entre las predicciones de nuestro modelo y el objetivo, utilizando pandas. La entrada más común es Verdadero, este es un buen indicador.
(test["Target"] == test["Predictions"]).describe()
unique 2
top True
freq 77409
dtype: object
Estimemos qué tan preciso es nuestro modelo.
#Our estimation of the model's accuracy ((test["Target"] == test["Predictions"]).describe().freq / (test["Target"] == test["Predictions"]).shape[0])
Nos interesa la precisión de cada una de las 10 zonas RSI.
val_err = []
Registra nuestra precisión en cada zona.
val_err.append(test.loc[(test["RSI_20"] < 10) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[test["RSI_20"] < 10].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 20) & (test["RSI_20"] > 10))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 30) & (test["RSI_20"] > 20))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 40) & (test["RSI_20"] > 30))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 50) & (test["RSI_20"] > 40))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 60) & (test["RSI_20"] > 50))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 70) & (test["RSI_20"] > 60))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 80) & (test["RSI_20"] > 70))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 90) & (test["RSI_20"] > 80))].shape[0]) val_err.append(test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90)) & (test["Predictions"] == test["Target"])].shape[0] / test.loc[((test["RSI_20"] <= 100) & (test["RSI_20"] > 90))].shape[0])
Trazando nuestra precisión. La línea roja es nuestro punto de corte del 50%, cualquier zona RSI debajo de esta línea puede no ser confiable. Podemos observar claramente que la última zona tiene una puntuación perfecta de 1. Sin embargo, recuerda que esto corresponde a la zona 91-100 faltante que no apareció ni una sola vez en más de 100.000 minutos de datos de entrenamiento que teníamos. Por lo tanto, es probable que esta zona sea difícil de ver y no sea óptima para nuestras necesidades comerciales. La zona 11-20 tiene niveles de precisión del 75%, los más altos de nuestras zonas alcistas. Lo mismo ocurrió con la zona 71-80, que tuvo la mayor precisión entre todas las zonas bajistas.
plt.plot(val_err)
plt.plot(fifty,'r') 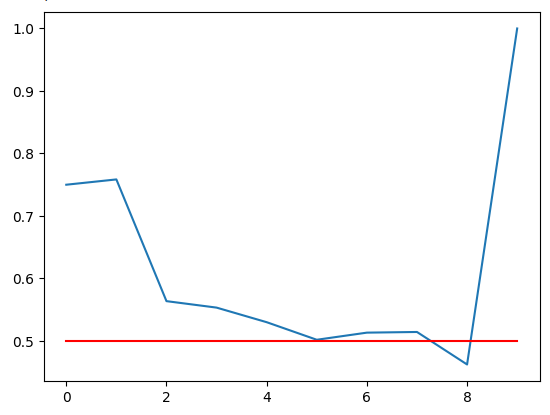
Figura 5: Visualización de nuestra precisión de validación.
Nuestra precisión de validación en las diferentes zonas RSI. Tenga en cuenta que obtuvimos una precisión del 100% en el rango 91-100. Recordemos que nuestro conjunto de entrenamiento fue de aproximadamente 100 000 filas, pero no observamos ninguna lectura de RSI en esa zona. Por lo tanto, podemos concluir que el precio rara vez alcanza esos extremos, por lo que el resultado puede no ser una decisión óptima para nosotros.
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 0.75 | 0.75 | 0.56 | 0.55 | 0.53 | 0.50 | 0.51 | 0.51 | 0.46 | 1.0 |
Construyendo nuestro modelo profundo de Markov
Hasta ahora, solo hemos construido un modelo que aprende de la distribución pasada de datos. ¿Sería posible que mejoráramos esta estrategia apilando un aprendiz más flexible, para aprender una estrategia óptima de uso de nuestro modelo de Markov? Entrenemos una red neuronal profunda y démosle las predicciones realizadas por el modelo de Markov como entradas, y los cambios observados en los niveles de precios serán el objetivo. Para realizar esta tarea de manera efectiva, necesitaremos subdividir nuestro conjunto de entrenamiento en 2 mitades. Ajustaremos nuestro nuevo modelo de Markov utilizando solo la primera mitad del conjunto de entrenamiento. Nuestra red neuronal se ajustará a las predicciones del modelo de Markov en el conjunto de entrenamiento de la primera mitad y a los cambios correspondientes en los niveles de precios.
Observamos que tanto nuestra red neuronal como nuestro modelo simple de Markov superaron a una red neuronal idéntica que intentaba aprender cambios en los niveles de precios directamente de las cotizaciones del mercado OHLC. Estas conclusiones se extrajeron a partir de nuestros datos de prueba que no se habían utilizado en el procedimiento de entrenamiento. Sorprendentemente, nuestra red neuronal profunda y nuestro modelo simple de Markov funcionaron al mismo nivel. Por lo tanto, esto puede verse como un llamado a un mayor esfuerzo para superar el punto de referencia establecido por el Modelo de Markov.
Comencemos importando las bibliotecas que necesitamos.
#Let us now try find a machine learning model to learn how to optimally use our transition matrix from sklearn.neural_network import MLPClassifier from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split,TimeSeriesSplit
Ahora necesitamos realizar una prueba de división del tren en nuestros datos de entrenamiento.
#Now let us partition our train set into 2 halves train , train_val = train_test_split(train,shuffle=False,test_size=0.5)
Coloque el modelo de Markov en el nuevo tren.
#Now let us recalculate our transition matrix, based on the first half of the training set rsi_matrix.iloc[0,0] = train.loc[(train["RSI_20"] < 10) & (train["Target"] == 1)].shape[0] / train.loc[(train["RSI_20"] < 10)].shape[0] rsi_matrix.iloc[0,1] = train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 10) & (train["RSI_20"] <=20))].shape[0] rsi_matrix.iloc[0,2] = train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 20) & (train["RSI_20"] <=30))].shape[0] rsi_matrix.iloc[0,3] = train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 30) & (train["RSI_20"] <=40))].shape[0] rsi_matrix.iloc[0,4] = train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 40) & (train["RSI_20"] <=50))].shape[0] rsi_matrix.iloc[0,5] = train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 50) & (train["RSI_20"] <=60))].shape[0] rsi_matrix.iloc[0,6] = train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 60) & (train["RSI_20"] <=70))].shape[0] rsi_matrix.iloc[0,7] = train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 70) & (train["RSI_20"] <=80))].shape[0] rsi_matrix.iloc[0,8] = train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90)) & (train["Target"] == 1)].shape[0] / train.loc[((train["RSI_20"] > 80) & (train["RSI_20"] <=90))].shape[0] rsi_matrix
| 0-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.655172 | 0.541701 | 0.536398 | 0.53243 | 0.516551 | 0.460306 | 0.491154 | 0.395349 | 0 |
Podemos visualizar esta distribución de probabilidad. Recuerde que estas cantidades representan la probabilidad de que los niveles de precios suban 20 minutos en el futuro, después de que el precio haya pasado por cada una de las 10 zonas RSI. La línea roja representa el nivel del 50%. Todas las zonas por encima del nivel del 50% son alcistas y todas las zonas por debajo son bajistas. Esto es lo que podemos asumir como cierto, dada la primera mitad de los datos de entrenamiento.
#From the training set, it appears that RSI readings above 61 are bearish and RSI readings below 61 are bullish plt.plot(rsi_matrix.iloc[0,:]) plt.plot(fifty,'r')
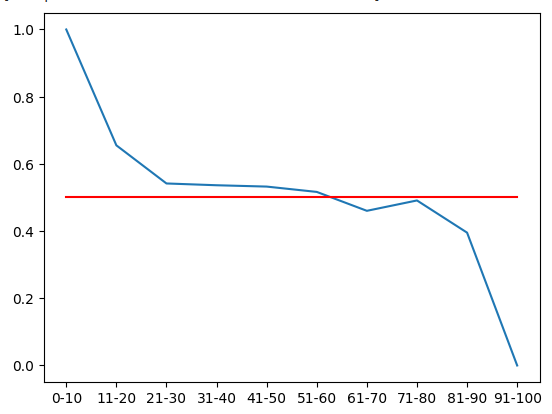
Figura 6: De la primera mitad del conjunto de entrenamiento, parece que todas las zonas por debajo de 61 son alcistas y por encima de 61 son bajistas.
Registrando las nuevas predicciones realizadas por el modelo de Markov.
#Let's now store our model's predictions train["Predictions"] = -1 train.loc[train["RSI_20"] < 61,"Predictions"] = 1 train_val["Predictions"] = -1 train_val.loc[train_val["RSI_20"] < 61,"Predictions"] = 1 test["Predictions"] = -1 test.loc[test["RSI_20"] < 61,"Predictions"] = 1
Antes de que podamos comenzar a utilizar redes neuronales, como regla general, es útil estandarizar y escalar. Además, nuestro RSI está en una escala fija de 0 a 100, mientras que nuestras lecturas de precios no tienen límites. En tales casos, la estandarización es necesaria.
#Let's Standardize and scale our data from sklearn.preprocessing import RobustScaler
Definir nuestras entradas y objetivos.
ohlc_predictors = ["open","high","low","close","tick_volume","spread","RSI_20"] transition_matrix = ["Predictions"] all_predictors = ohlc_predictors + transition_matrix target = ["Target"]
Escalar los datos.
scaler = RobustScaler() scaler = scaler.fit(train.loc[:,predictors]) train_scaled = pd.DataFrame(scaler.transform(train.loc[:,predictors]),columns=predictors) train_val_scaled = pd.DataFrame(scaler.transform(train_val.loc[:,predictors]),columns=predictors) test_scaled = pd.DataFrame(scaler.transform(test.loc[:,predictors]),columns=predictors)
Crear marcos de datos para almacenar nuestra precisión.
#Create a dataframe to store our cv error on the training set, validation training set and the test set train_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=np.arange(0,5)) train_val_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0]) test_err = pd.DataFrame(columns=["Transition Matrix","Deep Markov Model","OHLC Model","All Model"],index=[0])
Define el objeto de división de series de tiempo.
#Create a time series split object tscv = TimeSeriesSplit(n_splits = 5,gap=look_ahead)
Validar de forma cruzada los modelos.
model = MLPClassifier(hidden_layer_sizes=(20,10)) for i , (train_index,test_index) in enumerate(tscv.split(train_scaled)): #Fit the model model.fit(train.loc[train_index,transition_matrix],train.loc[train_index,"Target"]) #Record its accuracy train_err.iloc[i,1] = accuracy_score(train.loc[test_index,"Target"],model.predict(train.loc[test_index,transition_matrix])) #Record our accuracy levels on the validation training set train_val_err.iloc[0,1] = accuracy_score(train_val.loc[:,"Target"],model.predict(train_val.loc[:,transition_matrix])) #Record our accuracy levels on the test set test_err.iloc[0,1] = accuracy_score(test.loc[:,"Target"],model.predict(test.loc[:,transition_matrix])) #Our accuracy levels on the training set train_err
Observemos ahora la precisión de nuestro modelo en la mitad de validación del conjunto de entrenamiento.
train_val_err.iloc[0,0] = train_val.loc[train_val["Predictions"] == train_val["Target"]].shape[0] / train_val.shape[0] train_val_err
| Matriz de transición | Modelo de Markov profundo | Modelo OHLC | Todos los modelos |
|---|---|---|---|
| 0.52309 | 0.52309 | 0.507306 | 0.517291 |
Ahora, lo más importante es ver nuestra precisión en el conjunto de datos de prueba. Como podemos ver en las dos tablas, nuestro modelo híbrido de Markov profundo no logró superar a nuestro modelo de Markov simple. En mi opinión, esto me tomó por sorpresa. Esto podría implicar que nuestro procedimiento para entrenar la red neuronal profunda no fue óptimo, o bien siempre podemos buscar en un grupo más amplio de modelos de aprendizaje automático candidatos. Otro atributo interesante de nuestros resultados es que el modelo que utilizó todos los datos no tuvo el mejor desempeño.
La buena noticia es que logramos superar el índice de referencia establecido al intentar predecir el precio directamente a partir de las cotizaciones del mercado. Parece que la heurística simple del modelo de Markov ayuda a la red neuronal a aprender rápidamente la estructura del mercado de nivel inferior.
test_err.iloc[0,0] = test.loc[test["Predictions"] == test["Target"]].shape[0] / test.shape[0] test_err
| Matriz de transición | Modelo de Markov profundo | Modelo OHLC | Todos los modelos |
|---|---|---|---|
| 0.519322 | 0.519322 | 0.497127 | 0.496724 |
Implementación en MQL5
Para implementar nuestro Asesor Experto basado en RSI, comenzaremos importando las bibliotecas que necesitamos.
//+------------------------------------------------------------------+ //| Auto RSI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
Ahora definamos nuestras variables globales.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int rsi_handler; double rsi_buffer[]; int ma_handler; int system_state; double ma_buffer[]; double bid,ask; //--- Custom enumeration enum close_conditions { MA_Close = 0, RSI_Close };
Necesitamos obtener información de nuestros usuarios.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input group "Technical Indicators" input int rsi_period = 20; //RSI Period input int ma_period = 20; //MA Period input group "Money Management" input double trading_volume = 0.3; //Lot size input group "Trading Rules" input close_conditions user_close = RSI_Close; //How should we close the positions?
Cada vez que nuestro Asesor Experto se cargue por primera vez, carguemos los indicadores y validémoslos.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the indicator rsi_handler = iRSI(_Symbol,PERIOD_M1,rsi_period,PRICE_CLOSE); ma_handler = iMA(_Symbol,PERIOD_M1,ma_period,0,MODE_EMA,PRICE_CLOSE); //--- Validate our technical indicators if(rsi_handler == INVALID_HANDLE || ma_handler == INVALID_HANDLE) { //--- We failed to load the rsi Comment("Failed to load the RSI Indicator"); return(INIT_FAILED); } //--- return(INIT_SUCCEEDED); }
Si nuestra aplicación no está en uso, libere los indicadores.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release our technical indicators IndicatorRelease(rsi_handler); IndicatorRelease(ma_handler); }
Finalmente, no tenemos posiciones abiertas, utilizamos nuestras reglas de trading y seguimos nuestro modelo. De lo contrario, si tenemos una posición abierta, siga las instrucciones del usuario sobre cómo cerrar las operaciones.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market and technical data update(); //--- Check if we have any open positions if(PositionsTotal() == 0) { check_setup(); } if(PositionsTotal() > 0) { manage_setup(); } } //+------------------------------------------------------------------+
La siguiente función cerrará nuestras posiciones dependiendo de si el usuario quiere que utilicemos las reglas de trading que hemos aprendido del RSI o la media móvil simple. Si el usuario desea que utilicemos la media móvil, simplemente cerraremos nuestras posiciones siempre que el precio cruce la media móvil.
//+------------------------------------------------------------------+ //| Manage our open setups | //+------------------------------------------------------------------+ void manage_setup(void) { if(user_close == RSI_Close) { if((system_state == 1) && ((rsi_buffer[0] > 71) && (rsi_buffer[80] <= 80))) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } if((system_state == -1) && ((rsi_buffer[0] > 11) && (rsi_buffer[80] <= 20))) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } } else if(user_close == MA_Close) { if((iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0]) && (system_state == -1)) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } if((iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0]) && (system_state == 1)) { PositionSelect(Symbol()); Trade.PositionClose(PositionGetTicket(0)); return; } } }
La siguiente función verificará si tenemos alguna configuración válida. Es decir, si el precio ha entrado en alguna de nuestras zonas rentables. Además, si el usuario ha especificado que debemos utilizar la media móvil para cerrar nuestras posiciones, entonces esperaremos a que el precio esté en el lado derecho de la media móvil antes de decidir si debemos abrir una posición.
//+------------------------------------------------------------------+ //| Find if we have any setups to trade | //+------------------------------------------------------------------+ void check_setup(void) { if(user_close == RSI_Close) { if((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) { Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI"); system_state = -1; } if((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) { Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI"); system_state = 1; } } if(user_close == MA_Close) { if(((rsi_buffer[0] > 71) && (rsi_buffer[0] <= 80)) && (iClose(_Symbol,PERIOD_CURRENT,0) < ma_buffer[0])) { Trade.Sell(trading_volume,_Symbol,bid,0,0,"Auto RSI"); system_state = -1; } if(((rsi_buffer[0] > 11) && (rsi_buffer[0] <= 20)) && (iClose(_Symbol,PERIOD_CURRENT,0) > ma_buffer[0])) { Trade.Buy(trading_volume,_Symbol,ask,0,0,"Auto RSI"); system_state = 1; } } }
Esta función actualizará nuestros datos técnicos y de mercado.
//+------------------------------------------------------------------+ //| Fetch market quotes and technical data | //+------------------------------------------------------------------+ void update(void) { bid = SymbolInfoDouble(_Symbol,SYMBOL_BID); ask = SymbolInfoDouble(_Symbol,SYMBOL_ASK); CopyBuffer(rsi_handler,0,0,1,rsi_buffer); CopyBuffer(ma_handler,0,0,1,ma_buffer); } //+------------------------------------------------------------------+
Figura 7: Nuestro asesor experto.
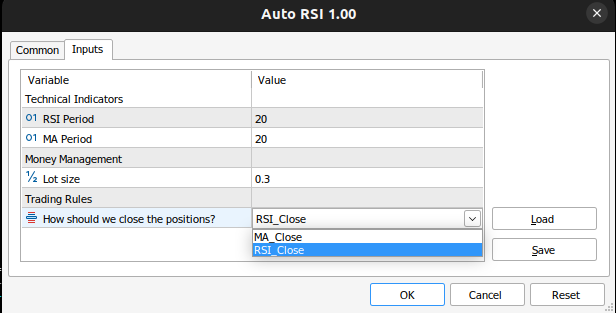
Figura 8: Nuestra aplicación de Asesor Experto.
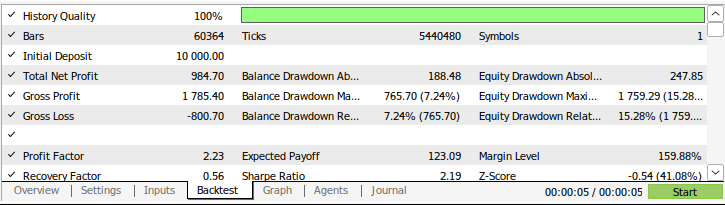
Figura 9: Los resultados de las pruebas retrospectivas de nuestra estrategia.
Conclusión
En este artículo, hemos demostrado el poder de los modelos probabilísticos simples. Para nuestra sorpresa, no pudimos superar el simple modelo de Markov intentando aprender de sus errores. Sin embargo, si usted ha seguido de cerca esta serie de artículos, probablemente compartirá mi punto de vista de que ahora vamos en la dirección correcta. Estamos acumulando lentamente un conjunto de algoritmos que son más fáciles de modelar que el precio en sí, bajo la restricción de ser tan informativos como el modelado del precio en sí. Únase a nosotros en nuestras próximas discusiones mientras intentamos aprender por qué será necesario superar el modelo simple de Markov.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/16030
 Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
Redes neuronales en el trading: Modelo hiperbólico de difusión latente (Final)
 Redes neuronales en el trading: Modelo hiperbólico de difusión latente (HypDiff)
Redes neuronales en el trading: Modelo hiperbólico de difusión latente (HypDiff)
 Reimaginando las estrategias clásicas en MQL5 (Parte IX): Análisis de múltiples marcos temporales (II)
Reimaginando las estrategias clásicas en MQL5 (Parte IX): Análisis de múltiples marcos temporales (II)
 De novato a experto: depuración colaborativa en MQL5
De novato a experto: depuración colaborativa en MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso