取引におけるニューラルネットワーク：一般化3次元指示表現セグメンテーション

MetaTrader 5 — トレーディングシステム | 26 5月 2025, 09:20

はじめに

3次元指示表現セグメンテーション(3D-RES: 3D Referring Expression Segmentation)は、マルチモーダル分野における新興領域として、研究者から大きな関心を集めています。このタスクでは、自然言語による指示に基づいて、ターゲットとなるインスタンスをセグメント化することに重点を置いています。しかし、従来の3D-RESアプローチは単一のターゲットにしか対応しておらず、実用上の適用範囲が大きく制限されています。実際の環境では、指示によってターゲットが見つからない場合や、複数のターゲットを同時に識別する必要がある状況が頻繁に発生します。このような現実は、既存の3D-RESモデルでは対応できない問題を引き起こします。このギャップを埋めるために、「 3D-GRES:Generalized 3D Referring Expression Segmentation」の著者らは、任意の数のターゲットを参照する命令を解釈するように設計された新しい手法、一般化3次元指示表現セグメンテーション(3D-GRES: Generalized 3D Referring Expression Segmentation)を提案しました。

3D-GRESの主な目的は、類似したオブジェクトの集合の中から複数のターゲットを正確に特定することです。このようなタスクを解決する鍵は、問題を分解し、複数のクエリがマルチオブジェクト指示のローカリゼーションを同時に処理できるようにすることです。各クエリは、複数のターゲットが存在するシーン内の1つのインスタンスを担当します。3D-GRESの著者らは、クエリ、スーパーポイント、テキスト間の相互作用を効率化するために設計されたモジュール「Multi-Query Decoupled Interaction Network (MDIN)」を導入しました。任意の数のターゲットを効果的に扱うために、複数のクエリが独立して動作しつつも、共同でマルチオブジェクト出力を生成できる仕組みが導入されています。この仕組みにおいて、各クエリはマルチインスタンス環境下における1つのターゲットを担当します。

点群内の主要なターゲットを学習可能なクエリによって均等にカバーするため、著者らは自然言語の指示表現を活用する新たなモジュール「Text-Guided Sparse Query (TSQ)」を提案しました。さらに、クエリ間の識別性を確保しつつ、全体として意味の一貫性を保つために、「Multi-Object Decoupling Optimization (MDO)」と呼ばれる最適化戦略を開発しました。この戦略では、マルチオブジェクトのマスクを個々の単一オブジェクトの監視信号に分解することで、各クエリの識別能力を維持します。。クエリ機能と、テキストセマンティクスと整合する点群内のスーパーポイント特徴との対応付けを通じて、複数のターゲット間で意味的な一貫性が確保されます。

1. 3D-GRESアルゴリズム

従来の3D-RESタスクは、参照表現に基づいて、点群シーン内の単一のターゲットオブジェクトに対する3Dマスクを生成することに焦点を当てています。この従来の定式化には、いくつかの重大な制約があります。第一に、点群内に指定された表現と一致するオブジェクトが存在しない場合には対応できません。第二に、複数のオブジェクトが表現された条件を満たすケースには対応していません。このように、モデルの能力と現実世界での適用性の間には大きなギャップがあり、それが3D-RES技術の実用的な利用を制限しています。

これらの制約を克服するために提案されたのが3次元指示表現セグメンテーション(3D-GRES)です。この手法は、テキストによる記述から任意の数のオブジェクトを識別できるように設計されています。3D-GRESでは、3D-GRES点群シーンPと参照表現Eを解析し、それに対応する3DマスクMを生成します。このマスクは、空の場合もあれば、1つ以上のオブジェクトを含む場合もあります。本手法により、複数ターゲットを含む表現によるオブジェクトの識別が可能となり、またターゲットオブジェクトが存在しないことを確認する「nothing」表現もサポートされるため、オブジェクトの検索および操作における柔軟性と堅牢性が大幅に向上します。

3D-GRESは、まず事前学習済みのRoBERTaモデルを用いて入力された参照表現をテキストトークン 𝒯 にエンコードします。マルチモーダルなアライメントを実現するために、エンコードされたトークンは次元数Dのマルチモーダル空間に射影され、さらに位置エンコーディングが適用されます。

入力点群（位置情報Pと特徴量Fを含む）に対しては、スパース3D U-Netを用いてスーパーポイントを抽出し、それらも同様にD次元のマルチモーダル空間に射影されます。

MDIN (Multi-Query Decoupled Interaction Network)は、複数のクエリを用いてマルチオブジェクトシーン内の各インスタンスを個別に処理し、それらを統合して最終的な結果を生成します。ターゲットオブジェクトが存在しないシーンでは、各クエリの信頼スコアに基づいて予測がおこなわれ、すべてのクエリの信頼度が低い場合はnull出力が予測されます。

MDINは、同一構成の複数のモジュールから構成されており、各モジュールは「Query-Superpoint Aggregation (QSA)」モジュールと「Query-Language Aggregation (QLA)」モジュールを含み、 クエリ、スーパーポイント、テキスト間の相互作用を可能にします。従来モデルがランダムにクエリを初期化していたのに対し、MDINではText-Guided Sparse Query (TSQ)モジュールを用いてテキストに基づくスパースなクエリを生成し、効率的なシーンカバレッジを実現しています。さらに、Multi-Object Decoupling Optimization (MDO)戦略によって、複数クエリの最適化が可能になります。

クエリは、点群空間内でのアンカーとして機能します。スーパーポイントとの相互作用を通じて、クエリは点群のグローバルな文脈を捉えます。特に、選択されたスーパーポイントはインタラクション過程においてクエリとしても機能し、ローカルな情報集約を強化します。このローカルな集約により、クエリの分離が効果的に促進されます。

最初に、スーパーポイント特徴量Sとクエリ埋め込みQfとの間の類似度分布が計算されます。クエリはこの類似度スコアに基づき、関連するスーパーポイントを集約します。こうして得られたシーン表現は、クエリ-クエリおよびクエリ-言語間の相互作用をモデル化するためにQLAモジュールへと渡されます。QLAは、クエリ特徴量Qsに対する自己アテンションブロックと、各単語と各クエリとの依存関係を捉えるためのマルチモーダルクロスアテンションブロックを含みます。

その後、関係コンテキストQr、言語対応特徴量Qlおよびシーン情報を含む特徴量Qsを合算し、MLPを通じて融合します。

クエリの初期化を点群シーン全体にスパースに分布させつつ、幾何学的および意味的な情報を保持するために、著者らはスーパーポイントに対してFarthest Point Samplingを直接適用しています。

クエリの分離と、それぞれを個別のオブジェクトに適切に割り当てるために、本手法ではTSQによって生成されるクエリの内在的な属性を活用します。各クエリは点群内の特定のスーパーポイントに由来しており、それによって自然に対応するオブジェクトにリンクされます。ターゲットインスタンスに関連付けられたクエリは、それらのインスタンスのセグメンテーションを担当し、関連のないオブジェクトは最も近いクエリに割り当てられます。このアプローチは、初期段階における視覚的制約を利用してクエリを分離し、それぞれを明確なターゲットに割り当てるものです。

著者らが提示した3D-GRES法の視覚的な概要は以下に示されています。

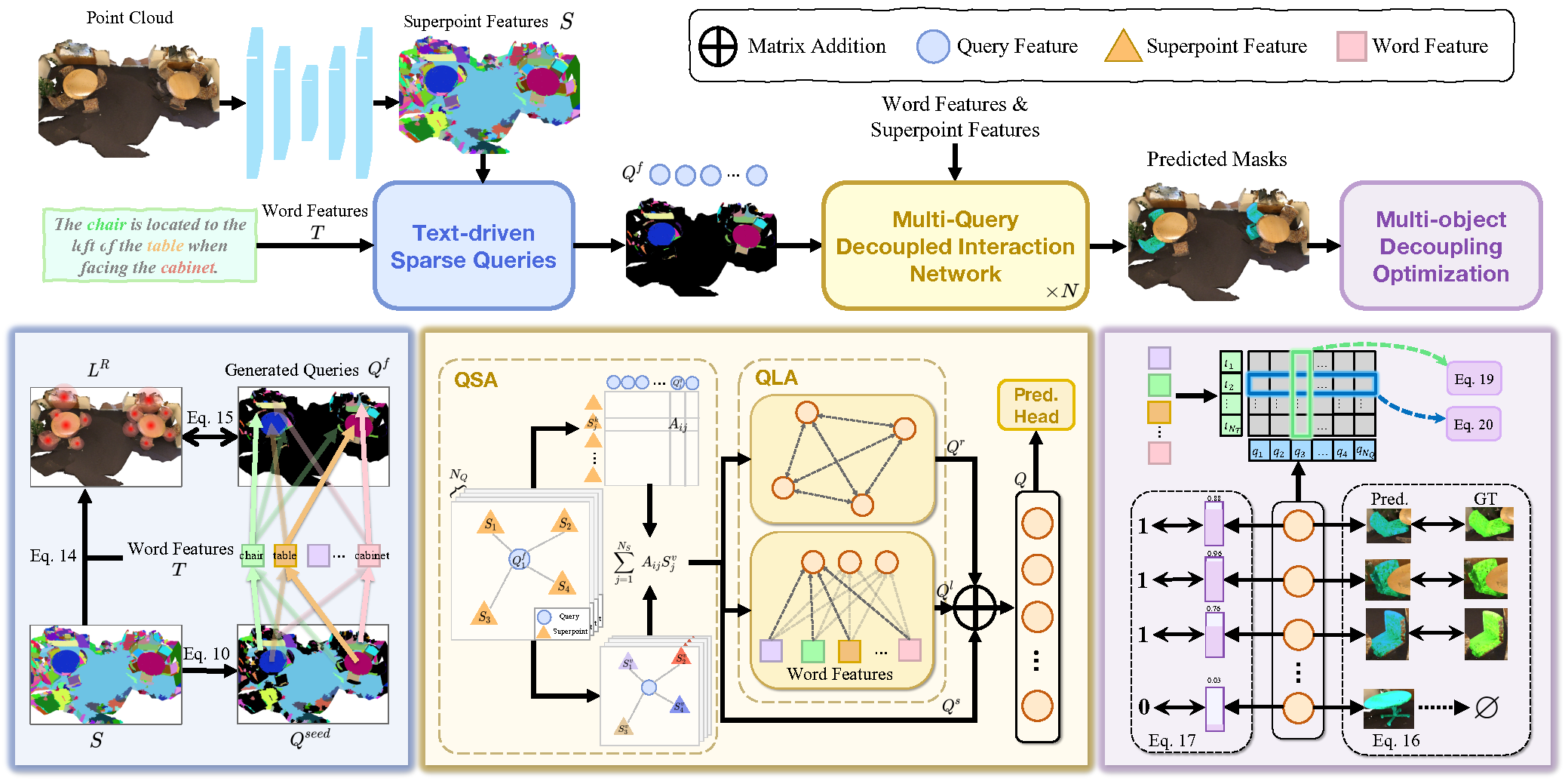
2.MQL5での実装

3D-GRES法の理論的側面について考察した後は、本稿の実用的な部分に移り、MQL5を使用して、提案するアプローチのビジョンを実装します。まず、3D-GRESアルゴリズムとこれまで検討してきた方法との違い、そして共通点について考えてみましょう。

まず注目すべきは、3D-GRESのマルチモダリティです。本手法では初めて、「参照表現(referring expressions)」が用いられ、分析の対象をより明確に特定しようとしています。このアイデアは、私たちの実装にも積極的に取り入れます。ただし、言語モデルを使用する代わりに、口座の状態や保有ポジションをモデルへの入力としてエンコードすることで対応します。これにより、口座の状態に基づいた埋め込みが、エントリーポイントやエグジットポイントの探索をモデルに促すことになります。

もう一つ重要な点は、学習可能なクエリの扱い方です。これまでに取り上げたモデルと同様に、3D-GRESも学習可能なクエリのセットを使用しています。ただし、そのクエリの形成原理には違いがあります。SPFormerやMAFTでは、学習中に最適化され、推論時には固定される静的なクエリが使われていました。つまり、これらのモデルは、あらかじめ学習されたパターンに基づいて、「準備されたスキーム」に従って動作していたのです。対照的に、3D-GRESの提案では、入力データに基づいてクエリを生成する方式が採用されており、より局所的で動的な性質を持っています。そして、分析対象のシーン空間を最適にカバーするために、さまざまなヒューリスティックが適用されています。私たちもこのアイデアを、実装に取り入れる予定です。

さらに、3D-GRESではトークンの位置エンコーディングが使用されます。これはMAFT法と共通しており、私たちが実装する際の親クラスの選定における基盤となっています。このような基礎をもとに、まずは私たちのOpenCLプログラムを拡張するところから始めます。

2.1 クエリの多様化

シーン空間を学習可能なクエリで最大限にカバーするために、クエリ同士が互いに「離れる」よう促す「多様性損失」を導入します。

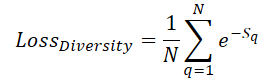
ここでSqはクエリqまでの距離を表します。明らかに、S =0の場合、損失は1になります。そして、クエリ間の平均距離が大きくなるにつれて、損失は0に近づいていきます。その結果、学習中にモデルはクエリをより均等に空間に分布させるようになります。

ただし、私たちが注目しているのは損失値そのものではなく、その勾配の向きです。勾配は、クエリ同士の距離を最大化するように各パラメータを調整するために利用されます。実装では、誤差勾配を即座に計算し、それを主なバックプロパゲーションの流れに組み込むことで、クエリのパラメータが最適化されるようにしています。このアルゴリズムは、DiversityLossカーネルに実装されています。

このカーネルは、2つのグローバルデータバッファと2つのスカラ変数を引数として受け取ります。最初のバッファには現在のクエリ特徴量が格納され、2つ目のバッファには多様性損失によって計算された勾配が保存されます。

__kernel void DiversityLoss(__global const float *data,
                            __global float *grad,
                            const int activation,
                            const int add
                           )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const size_t dim = get_local_id(2);
   const size_t total = get_local_size(1);
   const size_t dimension = get_local_size(2);

本カーネルは、3次元のワークスペース内で動作します。最初の2つの次元は解析対象のクエリ数に対応し、3つ目の次元は各クエリの特徴量ベクトルの次元数を表します。より低速なグローバルメモリへのアクセスを最小限に抑えるため、スレッドはタスク空間の後ろ2つの次元に沿ってワークグループに編成されます。

カーネル本体では、通常通り、まずグローバルタスク空間の3次元全体における現在のスレッドのインデックスを特定します。次に、ワークグループ内のスレッド間でのデータ共有を容易にするために、ローカルメモリ配列を宣言します。

   __local float Temp[LOCAL_ARRAY_SIZE];

また、解析対象の値にアクセスするために、グローバルデータバッファ内のオフセットも算出します。

   const int shift_main = main * dimension + dim;
   const int shift_slave = slave * dimension + dim;

その後、グローバルデータバッファから値を読み込み、それらの間の偏差を算出します。

   const int value_main = data[shift_main];
   const int value_slave = data[shift_slave];
   float delt = value_main - value_slave;

タスク空間およびワークグループは、各スレッドがグローバルメモリから読み込む値が2つだけになるように構成されています。次に、すべてのフローからの距離の総和を集計する必要があります。そのために、まずローカル配列の各要素に格納された個々の値を集約するループを構築します。

   for(int d = 0; d < dimension; d++)
     {
      for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE)
        {
         if(d == dim)
           {
            if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave)
              {
               int k = i % LOCAL_ARRAY_SIZE;
               float val = pow(delt, 2.0f) / total;
               if(isinf(val) || isnan(val))
                  val = 0;
               Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + val;
              }
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
     }

ここで注目すべき点として、最初は2つの値の単純な差分をdeltという変数に一時的に保存していることが挙げられます。そして、ローカル配列に距離を加算する直前にだけ、この値を2乗します。この設計は意図的なものであり、損失関数の導関数は差分そのものを必要とするためです。したがって、後の処理で冗長な再計算を避けるために、差分は元のまま保持しています。

次のステップでは、ローカル配列次のステップでは、ローカル配列に格納されたすべての値の総和を集計します。

   const int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);
   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count)
        {
         Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0);
         if(slave + count < ls)
            Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

その後で初めて、解析対象のクエリに対する多様性誤差の値と、対応する要素の誤差の勾配を計算します。

   float loss = exp(-Temp[0]);
   float gr = 2 * pow(loss, 2.0f) * delt / total;
   if(isnan(gr) || isinf(gr))
      gr = 0;

その後、解析対象クエリの各特徴量に関する誤差の勾配を集約するという、興味深いステップが待っています。誤差の勾配を合計するアルゴリズムは、前述の距離の合計処理と同様の方法で実装されます。

   for(int d = 0; d < dimension; d++)
     {
      for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE)
        {
         if(d == dim)
           {
            if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave)
              {
               int k = i % LOCAL_ARRAY_SIZE;
               Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + gr;
              }
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      //---
      int count = ls;
      do
        {
         count = (count + 1) / 2;
         if(slave < count && d == dim)
           {
            Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0);
            if(slave + count < ls)
               Temp[slave + count] = 0;
           }
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      if(slave == 0 && d == dim)
        {
         if(isnan(Temp[0]) || isinf(Temp[0]))
            Temp[0] = 0;
         if(add > 0)
            grad[shift_main] += Deactivation(Temp[0],value_main,activation);
         else
            grad[shift_main] = Deactivation(Temp[0],value_main,activation);
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

上記のアルゴリズムは、フィードフォワードとバックプロパゲーションの両方の処理を統合している点に注意が必要です。この統合によって、モデルの学習時にのみこのアルゴリズムを適用し、推論時にはこれらの処理を省略することが可能になります。その結果、この最適化は実運用環境における意思決定の速度向上に寄与します。

これでOpenCLプログラムの実装は完了となり、続いて3D-GRES法の中核的なアイデアを具現化するクラスの構築に移ります。

2.2 3D-GRESメソッドクラス

3D-GRES法で提案されたアプローチを実装するために、メインプログラムに新しいオブジェクトCNeuronGRESを作成します。前述のとおり、そのコア機能はCNeuronMAFTクラスから継承されます。新クラスの構造は以下のとおりです。

class CNeuronGRES :  public CNeuronMAFT
  {
protected:
   CLayer            cReference;
   CLayer            cRefKey;
   CLayer            cRefValue;
   CLayer            cMHRefAttentionOut;
   CLayer            cRefAttentionOut;
   //---
   virtual bool      CreateBuffers(void);
   virtual bool      DiversityLoss(CNeuronBaseOCL *neuron, const int units,
                                   const int dimension, const bool add = false);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                        CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None)
                                        override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronGRES(void) {};
                    ~CNeuronGRES(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_sp, uint units_sp, uint heads_sp,
                          uint ref_size, uint layers, uint layers_to_sp,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronGRES; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

コア機能に加えて、親クラスから多数の内部オブジェクトを継承することで、ほとんどの要件をカバーします。しかし、すべての要件を満たすわけではないため、残りのニーズに対応するために参照表現を処理するための追加オブジェクトを導入します。本クラス内のすべてのオブジェクトはstaticとして宣言しているため、コンストラクタとデストラクタは空で問題ありません。宣言および継承されたすべてのコンポーネントの初期化は、構築するオブジェクトのアーキテクチャを一意に定義するためのキー定数を受け取るInitメソッド内で行います。

bool CNeuronGRES::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count, uint heads,
                       uint window_sp, uint units_sp, uint heads_sp,
                       uint ref_size, uint layers, uint layers_to_sp,
                       ENUM_OPTIMIZATION optimization_type, uint batch
                      )
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

残念ながら、新クラスの構造は親クラスと大きく異なるため、継承したメソッドをそのまますべて再利用することはできません。これはInitメソッドの構造にも表れており、追加したコンポーネントだけでなく、継承したコンポーネントも手動で初期化する必要があります。

Initメソッド本体では、まず基底クラスの同名メソッドを呼び出します。これにより、入力パラメータの初期検証が行われ、モデル動作用のニューラル層間データ交換インターフェイスが有効化されます。

その後、受け取ったパラメータを本クラスの内部変数に格納します。

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;
   iSPUnits = units_sp;
   iSPWindow = window_sp;
   iSPHeads = heads_sp;
   iWindowKey = window_key;
   iLayers = MathMax(layers, 1);
   iLayersSP = MathMax(layers_to_sp, 1);

ここでは、さまざまなニューラル層のオブジェクトへのポインタを一時的に保存するためのいくつかの変数も宣言し、メソッド内で初期化します。

   CNeuronBaseOCL *base = NULL;
   CNeuronTransposeOCL *transp = NULL;
   CNeuronConvOCL *conv = NULL;
   CNeuronLearnabledPE *pe = NULL;

次に、学習可能クエリ生成モジュールの構築に移ります。まず、3D-GRESの著者らが入力点群に基づいて動的なクエリを生成することを提案していた点を思い出してください。しかし、解析対象となる点群は、要素数も各要素の特徴量ベクトル次元数も、学習可能クエリの集合とは異なる場合があります。この課題に対処するには、まず元のデータテンソルを転置してシーケンス中の要素配置を入れ替え、その後、畳み込み層を用いてシーケンスの要素数を目的の数に変換します。

//--- Init Querys
   cQuery.Clear();
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 0, OpenCL, iSPUnits, iSPWindow, optimization, iBatch) ||
      !cQuery.Add(transp))
      return false;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 1, OpenCL, iSPUnits, iSPUnits, iUnits, 1, iSPWindow, optimization, iBatch) ||
      !cQuery.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);

畳み込み層を利用することで、各特徴次元ごとに独立した一変量系列として並列かつ効率的にこの変換をおこなうことができます。

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, 2, OpenCL, iSPWindow, iUnits, optimization, iBatch) ||
      !cQuery.Add(transp))
      return false;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, 3, OpenCL, iSPWindow, iSPWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cQuery.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);

あとは、完全に学習可能な位置エンコーディングを組み込むだけです。

   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, 4, OpenCL, iWindow * iUnits, optimization, iBatch) ||
      !cQuery.Add(pe))
      return false;

親クラスのアルゴリズムと同様に、クエリの位置エンコーディング情報は別の情報フローとして扱います。

   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(0, 5, OpenCL, pe.Neurons(), optimization, iBatch) ||
      !base.SetOutput(pe.GetPE()) ||
      !cQPosition.Add(base))
      return false;

スーパーポイントモデルのアーキテクチャ生成アルゴリズムは、親クラスから一切変更せずにそのままコピーして利用しています。

//--- Init SuperPoints
   int layer_id = 6;
   cSuperPoints.Clear();
   for(int r = 0; r < 4; r++)
     {
      if(iSPUnits % 2 == 0)
        {
         iSPUnits /= 2;
         CResidualConv *residual = new CResidualConv();
         if(!residual ||
            !residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch) ||
            !cSuperPoints.Add(residual))
            return false;
        }
      else
        {
         iSPUnits--;
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, 
                                                                                                 iBatch) ||
            !cSuperPoints.Add(conv))
            return false;
         conv.SetActivationFunction(SIGMOID);
        }
      layer_id++;
     }
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch) ||
      !cSuperPoints.Add(conv))
      return false;
   conv.SetActivationFunction(SIGMOID);
   layer_id++;
   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch) ||
      !cSuperPoints.Add(pe))
      return false;
   layer_id++;

そして、参照表現の埋め込みを生成するためには、位置エンコーディング層を組み込んだ全結合MLPを使用します。

//--- Reference
   cReference.Clear();
   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(iWindow * iUnits, layer_id, OpenCL, ref_size, optimization, iBatch) ||
      !cReference.Add(base))
      return false;
   layer_id++;
   base = new CNeuronBaseOCL();
   if(!base ||
      !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) ||
      !cReference.Add(base))
      return false;
   base.SetActivationFunction(SIGMOID);
   layer_id++;
   pe = new CNeuronLearnabledPE();
   if(!pe ||
      !pe.Init(0, layer_id, OpenCL, base.Neurons(), optimization, iBatch) ||
      !cReference.Add(pe))
      return false;
   layer_id++;

MLPの出力は、学習可能クエリテンソルと次元整合したテンソルである点に留意してください。本設計により、参照表現を複数の意味的要素に分解し、現在の市場状況をより包括的に分析することができます。

ここまでで、入力データの主要処理を担うオブジェクトの初期化が完了しました。次は、内部のニューラル層オブジェクトを順次初期化するループ処理に移ります。その前に、クリーンなセットアップを保つために、内部オブジェクト格納用配列をクリアしておきます。

//--- Inside layers
   cQKey.Clear();
   cQValue.Clear();
   cSPKey.Clear();
   cSPValue.Clear();
   cSelfAttentionOut.Clear();
   cCrossAttentionOut.Clear();
   cMHCrossAttentionOut.Clear();
   cMHSelfAttentionOut.Clear();
   cMHRefAttentionOut.Clear();
   cRefAttentionOut.Clear();
   cRefKey.Clear();
   cRefValue.Clear();
   cResidual.Clear();
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1,optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;

ループ本体ではまず、クロスアテンション用のQuery Superpointオブジェクトを初期化します。具体的には、アテンションブロック向けのQueryエンティティ生成オブジェクトを生成します。その後、必要に応じてKeyエンティティ生成オブジェクトおよびValueエンティティ生成オブジェクトを追加します。

      if(l % iLayersSP == 0)
        {
         //--- Key
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                             optimization, iBatch) ||
            !cSPKey.Add(conv))
            return false;
         layer_id++;
         //--- Value
         conv = new CNeuronConvOCL();
         if(!conv ||
            !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                             optimization, iBatch) ||
            !cSPValue.Add(conv))
            return false;
         layer_id++;
        }

マルチヘッドアテンションの結果を記録するための層を追加します。

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHCrossAttentionOut.Add(base))
         return false;
      layer_id++;

結果のスケーリング層も追加します。

      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1,
                                                                                 optimization, iBatch) ||
         !cCrossAttentionOut.Add(conv))
         return false;
      layer_id++;

クロスアテンションブロックは、残差接続層で終了します。

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) ||
         !cResidual.Add(base))
         return false;
      layer_id++;

次のステップでは、クエリ間依存関係を分析しするために自己アテンションブロックを初期化します。ここでは、前のクロスアテンションブロックの結果に基づいてすべてのエンティティを生成します。

      //--- Self-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;
      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQValue.Add(conv))
         return false;
      layer_id++;

この場合、各内部層に対して、同じ数のアテンションヘッドを持つすべてのエンティティを生成します。

マルチヘッドアテンションの結果を記録するための層を追加します。

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHSelfAttentionOut.Add(base))
         return false;
      layer_id++;

結果のスケーリング層も追加します。

      //--- Self-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1,
                                                                                  optimization, iBatch) ||
         !cSelfAttentionOut.Add(conv))
         return false;
      layer_id++;

自己アテンションブロックと並行して、セマンティック参照表現向けのクエリクロスアテンションブロックがあります。ここでのQueryエンティティは、前のクロスアテンションブロックの結果に基づいて生成されます。

      //--- Reference Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cQuery.Add(conv))
         return false;
      layer_id++;

Key-Valueテンソルは、事前に準備されたセマンティック埋め込みから構成されます。

      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cRefKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) ||
         !cRefValue.Add(conv))
         return false;
      layer_id++;

自己アテンションブロックと同様に、それぞれの新しい層上のすべてのエンティティを、同じ数のアテンションヘッドで生成します。

次に、マルチヘッドアテンションの結果と結果のスケーリングの層を追加します。

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base ||
         !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
         !cMHRefAttentionOut.Add(base))
         return false;
      layer_id++;
      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0,layer_id, OpenCL, iWindowKey*iHeads, iWindowKey*iHeads, iWindow, iUnits, 1, 
                                                                             optimization, iBatch) ||
         !cRefAttentionOut.Add(conv))
         return false;
      layer_id++;
      if(!conv.SetGradient(((CNeuronBaseOCL*)cSelfAttentionOut[cSelfAttentionOut.Total() - 1]).getGradient(),
                                                                                                        true))
         return false;

このブロックは、3つのアテンションブロックすべての結果を結合する残差接続層によって完了します。

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

強化されたクエリの最終処理は、残差接続を持つFeedForwardブロックに実装されます。その構造はバニラTransformerに似ています。

      //--- Feed Forward
      conv = new CNeuronConvOCL();
      if(!conv || 
         !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4*iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      conv = new CNeuronConvOCL();
      if(!conv ||
         !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

さらに、親クラスからオブジェクト中心位置補正のアルゴリズムを移植します。なお、このアルゴリズムは3D-GRES法の著者によって提供されたものです。

      //--- Delta position
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(SIGMOID);
      if(!cQPosition.Add(conv))
         return false;
      layer_id++;
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cQPosition.Add(base))
         return false;
      layer_id++;
     }

次に、内部層のオブジェクトを生成するループの次の反復に移ります。ループの全反復が完了したら、データバッファへのポインタを差し替えます。これにより、データのコピー回数を削減し、学習プロセスを高速化できます。

   base = cResidual[iLayers * 3 - 1];
   if(!SetGradient(base.getGradient()))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

メソッドの処理の最後に、実行したステップの成功・失敗を示すブール値を呼び出し元プログラムに返します。

前回の記事と同様に、補助データバッファの作成処理はCreateBuffersという別メソッドに切り出しています。このメソッドについては別途ご確認ください。完全なソースコードは添付ファイルにあります。

新しいクラスのオブジェクトが初期化されたら、feedForwardメソッドで実装されるフィードフォワードパスアルゴリズムの構築に進みます。今回は、このメソッドが2つの入力データオブジェクトへのポインタを受け取ります。1つは解析対象の点群データ、もう1つは参照表現を表しています。

bool CNeuronGRES::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
//--- Superpoints
   CNeuronBaseOCL *superpoints = NeuronOCL;
   int total_sp = cSuperPoints.Total();
   for(int i = 0; i < total_sp; i++)
     {
      if(!cSuperPoints[i] ||
         !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints))
         return false;
      superpoints = cSuperPoints[i];
     }

メソッドの本体では、すぐに小規模なスーパーポイント生成モデルのフィードフォワードループを構成します。同様に、クエリを生成します。

//--- Query
   CNeuronBaseOCL *query = NeuronOCL;
   for(int i = 0; i < 5; i++)
     {
      if(!cQuery[i] ||
         !((CNeuronBaseOCL*)cQuery[i]).FeedForward(query))
         return false;
      query = cQuery[i];
     }

参照表現の意味埋め込みテンソルを生成するには、もう少し手間がかかります。参照表現は生データバッファとして受け取りますが、フィードフォワードパスの内部モジュールはニューラル層オブジェクトを入力として想定しています。そこで、メインモデルでの入力処理と同様に、内部セマンティック埋め込み生成モデルの最初の層を入力データ受け取り用のプレースホルダーとして利用します。ただし、この場合はバッファ内容を丸ごとコピーするのではなく、基のデータポインタをバッファのものに差し替えます。

//--- Reference
   CNeuronBaseOCL *reference = cReference[0];
   if(!SecondInput)
      return false;
   if(reference.getOutput() != SecondInput)
      if(!reference.SetOutput(SecondInput, true))
         return false;

次に、内部モデルのフィードフォワードループを実行します。

   for(int i = 1; i < cReference.Total(); i++)
     {
      if(!cReference[i] ||
         !((CNeuronBaseOCL*)cReference[i]).FeedForward(reference))
         return false;
      reference = cReference[i];
     }

これで元データの事前処理が完了し、メインのデータデコードアルゴリズムに進むことができます。そのために、デコーダの内部層を順に処理するループを構成します。

   CNeuronBaseOCL *inputs = query, *key = NULL, *value = NULL, *base = NULL, *cross = NULL, *self = NULL;
//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Calc Position bias
      cross = cQPosition[l * 2];
      if(!cross ||
         !CalcPositionBias(cross.getOutput(),
                           ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l],
                           iUnits, iSPUnits, iWindow))
         return false;

まず、MAFT法で用いられた手法に従い、位置オフセット係数を定義します。これは、3D-GRESの元のアルゴリズムにおいて著者らがアテンションマスク生成にMLPを用いていた点からの変更となります。

次に、クエリとスーパーポイント間の依存関係をモデル化する役割を持つクロスアテンションブロックQSAに進みます。このブロックでは、まずQuery、Key、Valueの各エンティティのテンソルを生成します。KeyとValueは必要な場合のみ生成されます。

      //--- Cross-Attention
      query = cQuery[l * 3 + 5];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cSPKey[l / iLayersSP];
      value = cSPValue[l / iLayersSP];
      if(l % iLayersSP == 0)
        {
         if(!key || !key.FeedForward(superpoints))
            return false;
         if(!value || !value.FeedForward(cSuperPoints[total_sp - 2]))
            return false;
        }

次に、位置バイアス係数を考慮して依存関係を解析します。

      if(!AttentionOut(query, key, value, cScores[l * 3], cMHCrossAttentionOut[l], cPositionBias[l],
                                               iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true))
         return false;

マルチヘッドアテンションの結果にスケーリングをおこない、残差接続の値を加えた後、データの正規化を実施します。

      base = cCrossAttentionOut[l];
      if(!base || !base.FeedForward(cMHCrossAttentionOut[l]))
         return false;
      value = cResidual[l * 3];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1)||
         !SumAndNormilize(cross.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

次のステップでは、QLAモジュールの操作を整理します。ここでは、フィードフォワードパスの2つのアテンションブロックを整理する必要があります。

自己アテンション → クエリ-クエリ
クロスアテンション → クエリ-参照

まず、自己アテンションブロックの操作を実装します。ここでは、前のデコーダブロックから受信したデータに基づいてQuery、Key、Valueエンティティテンソルを完全に生成します。

      //--- Self-Atention
      query = cQuery[l * 3 + 6];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cQKey[l];
      if(!key || !key.FeedForward(inputs))
         return false;
      value = cQValue[l];
      if(!value || !value.FeedForward(inputs))
         return false;

次に、標準のマルチヘッドアテンションモジュール内の依存関係を分析します。

      if(!AttentionOut(query, key, value, cScores[l * 3 + 1], cMHSelfAttentionOut[l], -1, 
                                        iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;
      self = cSelfAttentionOut[l];
      if(!self || !self.FeedForward(cMHSelfAttentionOut[l]))
         return false;

その後、得られた結果をスケーリングします。

クロスアテンションブロックも同様の方法で構築されます。唯一の違いは、KeyとValueのエンティティが参照表現のセマンティック埋め込みから生成されることです。

      //--- Reference Cross-Attention
      query = cQuery[l * 3 + 7];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cRefKey[l];
      if(!key || !key.FeedForward(reference))
         return false;
      value = cRefValue[l];
      if(!value || !value.FeedForward(reference))
         return false;
      if(!AttentionOut(query, key, value, cScores[l * 3 + 2], cMHRefAttentionOut[l], -1, 
                                       iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;
      cross = cRefAttentionOut[l];
      if(!cross || !cross.FeedForward(cMHRefAttentionOut[l]))
         return false;

次に、3つのアテンションブロックすべての結果を合計し、取得したデータを正規化します。

      value = cResidual[l * 3 + 1];
      if(!value ||
         !SumAndNormilize(cross.getOutput(), self.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1) ||
         !SumAndNormilize(inputs.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

次に、残差接続とデータの正規化を備えたバニラTransformerのFeedForwardブロックが続きます。

      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.FeedForward(inputs))
         return false;
      base = cFeedForward[l * 2 + 1];
      if(!base || !base.FeedForward(cFeedForward[l * 2]))
         return false;
      value = cResidual[l * 3 + 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

ご覧のとおり、構築したフィードフォワードパスのアルゴリズムは、3D-GRESとMAFTのハイブリッドのような構成になっています。したがって、最後にMAFT法から仕上げの要素、つまりクエリ位置の調整を加えるだけです。

      //--- Delta Query position
      base = cQPosition[l * 2 + 1];
      if(!base ||
         !base.FeedForward(inputs))
         return false;
      value = cQPosition[(l + 1) * 2];
      query = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0,0.5f))
         return false;
     }

その後、次のデコーダ層に進みます。デコーダのすべての内部層での反復処理を完了した後、強化されたクエリ値とその位置エンコーディングを合計します。基本インターフェイスを介して結果をモデルの次の層に渡します。

   value = cQPosition[iLayers * 2];
   if(!value ||
      !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

この時点で、処理が正常に完了したかどうかを示すブール値の結果を呼び出し元プログラムに返します。

これで、フィードフォワードパスの実装が完了したので、バックプロパゲーションアルゴリズムの実装に進みます。通常どおり、この処理は2つのステージに分かれます。

勾配の伝播(calcInputGradients)
モデルパラメータの最適化(updateInputWeights)

最初のステージでは、順伝播時の操作を逆順にたどりながら、誤差の勾配を逆伝播させていきます。次のステージでは、学習可能なパラメータを含む内部層に対して、それぞれの更新メソッドを呼び出します。一見すると、これはよくある標準的な流れに見えます。ただし、クエリの多様化に関連する特有の処理があります。したがって、誤差の勾配を伝播するcalcInputGradientsメソッドの実装を、少し詳しく見ていきましょう。

このメソッドは、3つのデータオブジェクトへのポインタと、2番目の入力ソースで使用されている活性化関数を指定する定数をパラメータとして受け取ります。

bool CNeuronGRES::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                     CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient)
      return false;

メソッド本体では、ポインタのうち2つのみを検証します。フィードフォワードパス中に、2番目の入力ソースへのポインタはすでに保存してあるため、この段階でそのポインタがパラメータとして有効でないことは、私たちにとって致命的ではありません。しかし、誤差の勾配を格納するためのバッファについては話が別です。したがって、処理を進める前にその有効性を明示的にチェックします。

この段階で、関連オブジェクトへのポインタを一時的に保持するための変数もいくつか宣言します。これで実装の準備段階は完了です。

   CNeuronBaseOCL *residual = GetPointer(this), *query = NULL, *key = NULL, *value = NULL,
                   *key_sp = NULL, *value_sp = NULL, *base = NULL;

次に、デコーダの内部層を通る逆ループを構成します。

//--- Inside layers
   for(int l = (int)iLayers - 1; l >= 0; l--)
     {
      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.calcHiddenGradients(cFeedForward[l * 2 + 1]))
         return false;
      base = cResidual[l * 3 + 1];
      if(!base || !base.calcHiddenGradients(cFeedForward[l * 2]))
         return false;

内部オブジェクト内でバッファポインタをうまく置き換えることで、不要なデータコピー操作を回避できています。そのため、まずはFeedForwardブロックを通じて誤差の勾配を伝播させる処理から開始します。

FeedForwardブロックの入力レベルで得られた誤差の勾配は、本クラスの出力レベルにおける対応する値と加算されます。これは、このブロック内の残差データフローと整合しています。これらの操作の結果は、そのまま自己アテンションブロックの結果バッファへと渡されます。

      //--- Residual
      value = cSelfAttentionOut[l];
      if(!value ||
         !SumAndNormilize(base.getGradient(), residual.getGradient(), value.getGradient(), iWindow, false,
                                                                                              0, 0, 0, 1))
         return false;
      residual = value;

FeedForwardブロックへの入力は、3つのアテンションブロックの出力を合算したもので構成されています。したがって、得られた誤差の勾配は、それぞれのソースへと逆伝播させる必要があります。データを合算したのと同様に、勾配も各コンポーネントに対してそのまま全量を伝播します。なお、QSAブロックの出力はデコーダ内の他のモジュールの入力としても使用されているため、同様に残差的なデータフローのロジックに従って、対応する誤差の勾配は後段で累積処理されることになります。また、クエリ-参照クロスアテンションブロックへの誤差の勾配を冗長にコピーしないよう、オブジェクト初期化時にポインタの差し替えをあらかじめおこなっておきました。その結果、自己アテンションブロックにデータを渡すタイミングで、同じ勾配データをクエリ-参照クロスアテンションブロックにも同時に渡すことができます。この小さな最適化によって、メモリ使用量と学習時間の削減が実現されます。

次に、クエリ-参照クロスアテンションブロックを通じて誤差の勾配の伝播処理を進めていきます。

      //--- Reference Cross-Attention
      base = cMHRefAttentionOut[l];
      if(!base || !base.calcHiddenGradients(cRefAttentionOut[l], NULL))
         return false;
      query = cQuery[l * 3 + 7];
      key = cRefKey[l];
      value = cRefValue[l];
      if(!AttentionInsideGradients(query, key, value, cScores[l * 3 + 2], base, 
                                    iUnits, iHeads, iUnits, iHeads, iWindowKey))
         return false;

Queryエンティティからの誤差の勾配をQSAモジュールに渡します。その前に、FeedForwardブロック（残差接続のフロー）から取得した誤差の勾配を追加します。

      base = cResidual[l * 3];
      if(!base || !base.calcHiddenGradients(query, NULL))
         return false;
      value = cCrossAttentionOut[l];
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(),value.getGradient(), iWindow, false,
                                                                                               0, 0, 0, 1))
         return false;
      residual = value;

同様に、誤差の勾配を自己アテンションブロックに渡します。

      //--- Self-Attention
      base = cMHSelfAttentionOut[l];
      if(!base || !base.calcHiddenGradients(cSelfAttentionOut[l], NULL))
         return false;
      query = cQuery[l * 3 + 6];
      key = cQKey[l];
      value = cQValue[l];
      if(!AttentionInsideGradients(query, key, value, cScores[l * 2 + 1], base, 
                                     iUnits, iHeads, iUnits, iHeads, iWindowKey))
         return false;

続いて、QSAモジュールに対して、3つのエンティティすべてからの誤差の勾配を加算する必要があります。そのために、まずはそれぞれの誤差の勾配を順に残差接続層のレベルまで逆伝播させ、得られた値をこれまでに累積されてきたQSAモジュールの勾配の合計に加算していきます。

      base = cResidual[l * 3 + 1];
      if(!base.calcHiddenGradients(query, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(key, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(value, NULL))
         return false;
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 
                                                                                                  0, 0, 0, 1))
         return false;

また、蓄積された勾配値の合計を、クエリの位置エンコーディングからの並列情報フローに渡し、別の情報フローからの勾配と加算します。

      //--- Qeury position
      base = cQPosition[l * 2];
      value = cQPosition[(l + 1) * 2];
      if(!base ||
         !SumAndNormilize(value.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false,
                                                                                               0, 0, 0, 1))
         return false;

そして最後に、QSAモジュールを通じて誤差の勾配を伝播させる必要があります。ここでは、アテンションブロックを通じて誤差の勾配を伝播させる際と同じアルゴリズムを使用しますが、デコーダの複数の層にわたるKeyおよびValueエンティティの誤差勾配に対応するための調整を加えます。まず、一時的なデータバッファに誤差の勾配を集め、それから対応するオブジェクトのバッファに結果を保存します。

      //--- Cross-Attention
      base = cMHCrossAttentionOut[l];
      if(!base || !base.calcHiddenGradients(residual, NULL))
         return false;
      query = cQuery[l * 3 + 5];
      if(((l + 1) % iLayersSP) == 0 || (l + 1) == iLayers)
        {
         key_sp = cSPKey[l / iLayersSP];
         value_sp = cSPValue[l / iLayersSP];
         if(!key_sp || !value_sp ||
            !cTempCrossK.Fill(0) || !cTempCrossV.Fill(0))
            return false;
        }
      if(!AttentionInsideGradients(query, key_sp, value_sp, cScores[l * 2], base, 
                                                           iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey))
         return false;
      if(iLayersSP > 1)
        {
         if((l % iLayersSP) == 0)
           {
            if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), key_sp.getGradient(), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
            if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), value_sp.getGradient(), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
         else
           {
            if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), GetPointer(cTempCrossK), 
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
            if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), GetPointer(cTempCrossV),
                                                                           iWindowKey, false, 0, 0, 0, 1))
               return false;
           }
        }

Queryエンティティからの誤差の勾配は、初期データのレベルに伝播されます。ここでは、残差接続の情報フローに関するデータも追加します。その後、デコーダ層を通る逆ループの次の反復に進みます。

      if(l == 0)
         base = cQuery[4];
      else
         base = cResidual[l * 3 - 1];
      if(!base || !base.calcHiddenGradients(query, NULL))
         return false;
      //--- Residual
      if(!SumAndNormilize(base.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false,
                                                                                              0, 0, 0, 1))
         return false;
      residual = base;
     }

デコーダのすべての層を通じて誤差の勾配を正常に伝播させた後は、データ前処理モジュールの各処理を経由して、この勾配を元の入力データレベルまで伝播させる必要があります。まず、学習可能なクエリから誤差の勾配を伝播します。そのために、誤差の勾配を位置エンコーディング層に通します。

//--- Qeury
   query = cQuery[3];
   if(!query || !query.calcHiddenGradients(cQuery[4]))
      return false;

この段階では、対応する情報フローから位置コーディングの誤差の勾配を注入します。

   base = cQPosition[0];
   if(!DeActivation(base.getOutput(), base.getGradient(), base.getGradient(), SIGMOID) ||
      !(((CNeuronLearnabledPE*)cQuery[4]).AddPEGradient(base.getGradient())))
      return false;

次に、クエリの多様化誤差に関する勾配を加えますが、この処理では位置エンコーディングに関する情報は使用しません。このステップは意図的に行われており、多様化誤差が位置エンコーディングに影響を与えないようにするためです。

   if(!DiversityLoss(query, iUnits, iWindow, true))
      return false;

続いて、クエリ生成モデルの各層を逆順に処理するシンプルなループをおこない、誤差の勾配を入力データのレベルまで伝播させます。

   for(int i = 2; i >= 0; i--)
     {
      query = cQuery[i];
      if(!query || !query.calcHiddenGradients(cQuery[i + 1]))
         return false;
     }
   if(!NeuronOCL.calcHiddenGradients(query, NULL))
      return false;

ここで注目すべきは、誤差の勾配は内部のスーパーポイント生成モデルの入力レベルにも伝播させる必要があるという点です。データ損失を防ぐために、入力データオブジェクトの勾配バッファへのポインタをローカル変数に保持します。その後、クエリ生成モデルの転置層の勾配バッファと置き換えます。

転置層には学習可能なパラメータが含まれていないため、その誤差の勾配が失われても問題はありません。

   CBufferFloat *inputs_gr = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(query.getGradient(), false))
      return false;

次のステップは、スーパーポイント生成モデルを通じて誤差の勾配を伝播することです。ただし、デコーダ層の逆伝播時には、このモデルへは勾配が伝播されていないことに注意が必要です。したがって、まず対応するKeyおよびValueエンティティから誤差の勾配を収集しなければなりません。各エンティティに対して少なくとも1つのテンソルが存在することはわかっていますが、もうひとつ重要な点があります。Keyエンティティは、位置エンコーディングを含むスーパーポイントモデルの最終層の出力から生成されているのに対し、Valueエンティティは位置エンコーディングなしの最終層手前の層から取得されています。したがって、誤差の勾配はこれら特定のデータ経路に沿って伝播させる必要があります。

まず、Keyエンティティの最初の層の誤差の勾配を計算し、それを内部モデルの最終層に渡します。

//--- Superpoints
//--- From Key
   int total_sp = cSuperPoints.Total();
   CNeuronBaseOCL *superpoints = cSuperPoints[total_sp - 1];
   if(!superpoints || !superpoints.calcHiddenGradients(cSPKey[0]))
      return false;

次に、Keyエンティティ層の数を確認し、必要に応じて、以前に取得した誤差の勾配の損失を防ぐために、データバッファを置き換えます。

   if(cSPKey.Total() > 1)
     {
      CBufferFloat *grad = superpoints.getGradient();
      if(!superpoints.SetGradient(GetPointer(cTempSP), false))
         return false;

そして、このエンティティの残りの層を順にループ処理し、誤差の勾配を計算してから、以前に蓄積された値と結果を合算します。

      for(int i = 1; i < cSPKey.Total(); i++)
        {
         if(!superpoints.calcHiddenGradients(cSPKey[i]) ||
            !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1))
            return false;
        }

すべてのループ反復が正常に完了したら、累積された誤差の勾配の合計を含むバッファへのポインタを返します。

      if(!superpoints.SetGradient(grad, false))
         return false;
     }

こうして、スーパーポイントモデルの最終層でKeyエンティティの全層から誤差の勾配を集約できたため、これを指定モデルの一つ下のレベルへ伝播させることができます。

   superpoints = cSuperPoints[total_sp - 2];
   if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[total_sp - 1]))
      return false;

そして、同じレベルでValueエンティティからの誤差の勾配も集約する必要があります。ここでは同じアルゴリズムを使用します。ただし、今回の誤差勾配バッファにはすでに後続層から受け取ったデータが存在するため、まずデータバッファを差し替え、その後ループ内で並列データストリームから情報を集約します。

//--- From Value
   CBufferFloat *grad = superpoints.getGradient();
   if(!superpoints.SetGradient(GetPointer(cTempSP), false))
      return false;
   for(int i = 0; i < cSPValue.Total(); i++)
     {
      if(!superpoints.calcHiddenGradients(cSPValue[i]) ||
         !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1))
         return false;
     }
   if(!superpoints.SetGradient(grad, false))
      return false;

次に、多様化誤差も追加します。これにより、スーパーポイントを可能な限り多様化することができます。

   if(!DiversityLoss(superpoints, iSPUnits, iSPWindow, true))
      return false;

次に、スーパーポイントモデル層を経由する逆ループで、誤差の勾配を入力データのレベルに伝播します。

   for(int i = total_sp - 3; i >= 0; i--)
     {
      superpoints = cSuperPoints[i];
      if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[i + 1]))
         return false;
     }
//--- Inputs
   if(!NeuronOCL.calcHiddenGradients(cSuperPoints[0]))
      return false;

ここで思い出していただきたいのは、クエリ情報フローの処理後に入力レベルで一部の誤差の勾配を保持していたことです。その際、データバッファの置き換えをおこないました。そして今、両方の情報フローの誤差の勾配を合算します。最後に、データバッファへのポインタを元に戻します。

   if(!SumAndNormilize(NeuronOCL.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
      return false;
   if(!NeuronOCL.SetGradient(inputs_gr, false))
      return false;

このようにして、最初の入力データソースに対して2つの情報フローからの誤差の勾配を収集しました。しかし、まだ誤差の勾配を2番目の入力データオブジェクトへ伝播させる必要があります。そのために、まず2番目の入力データオブジェクトの誤差勾配バッファと、参照モデルの第一層の誤差勾配バッファのポインタを同期させます。

   base = cReference[0];
   if(base.getGradient() != SecondGradient)
     {
      if(!base.SetGradient(SecondGradient))
         return false;
      base.SetActivationFunction(SecondActivation);
     }

次に、指定されたモデルの最終層で、対応するKeyおよびValueエンティティのすべてのテンソルから誤差の勾配を収集します。アルゴリズムは先述のものと類似しています。

   base = cReference[2];
   if(!base ||
      !base.calcHiddenGradients(cRefKey[0]))
      return false;
   inputs_gr = base.getGradient();
   if(!base.SetGradient(GetPointer(cTempQ), false))
      return false;
   if(!base.calcHiddenGradients(cRefValue[0]))
      return false;
   if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
      return false;
   for(uint i = 1; i < iLayers; i++)
     {
      if(!base.calcHiddenGradients(cRefKey[i]))
         return false;
      if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
         return false;
      if(!base.calcHiddenGradients(cRefValue[i]))
         return false;
      if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1))
         return false;
     }
   if(!base.SetGradient(inputs_gr, false))
      return false;

位置エンコーディング層を通じて誤差の勾配を伝播します。

   base = cReference[1];
   if(!base.calcHiddenGradients(cReference[2]))
      return false;

さらに、セマンティックコンポーネントの多様性を最大限に確保するために、ベクトルの多様化誤差を追加します。

   if(!DiversityLoss(base, iUnits, iWindow, true))
      return false;

その後、誤差の勾配を入力データレベルに伝播します。

   base = cReference[0];
   if(!base.calcHiddenGradients(cReference[1]))
      return false;
//---
   return true;
  }

メソッドの最後に、実行された操作の論理結果を呼び出し元プログラムに返します。

これで、新しいクラスに実装されたアルゴリズムメソッドの解説を終わります。このクラスとそのすべてのメソッドの完全なソースコードは添付ファイルにあり、そこでモデルアーキテクチャや、本記事作成時に使用したプログラムの詳細な説明もご覧いただけます。

学習可能なモデルのアーキテクチャは、以前の研究成果からほぼそのまま継承されています。唯一の変更点は、環境状態を記述するエンコーダの一部の層に対して加えたものです。

加えて、モデルの学習プログラムおよび環境とのインタラクションロジックにも小規模な更新がおこなわれました。これらは、環境状態エンコーダに第2のデータソースを渡す必要があったためであり、的を絞った最小限の修正です。前述のとおり、参照表現として口座状態ベクトルを用いていますが、このベクトルの準備処理はActorモデルで既に実装済みでした。

3.テスト

私たちは多大な作業を経て、MQL5を用いて3D-GRES法とMAFT法のアプローチを組み合わせたハイブリッドシステムを構築しました。いよいよ結果の評価をおこないます。今回の課題は、提案した技術を実際の履歴データでモデルに学習させ、その学習済みActorポリシーのパフォーマンスを評価することです。

これまでと同様に、モデルの訓練にはEURUSDの実際の履歴データ（H1時間枠、2023年全期間）を使用します。すべてのインジケーターのパラメータはデフォルト値のままとしています。

学習プロセス中に、以前の研究で検証されたアルゴリズムを適用しました。

学習済みのActor方策は、MetaTrader 5のストラテジーテスターで2024年1月の過去データを用いてテストしました。それ以外のパラメータは変更していません。以下にそのテスト結果を示します。

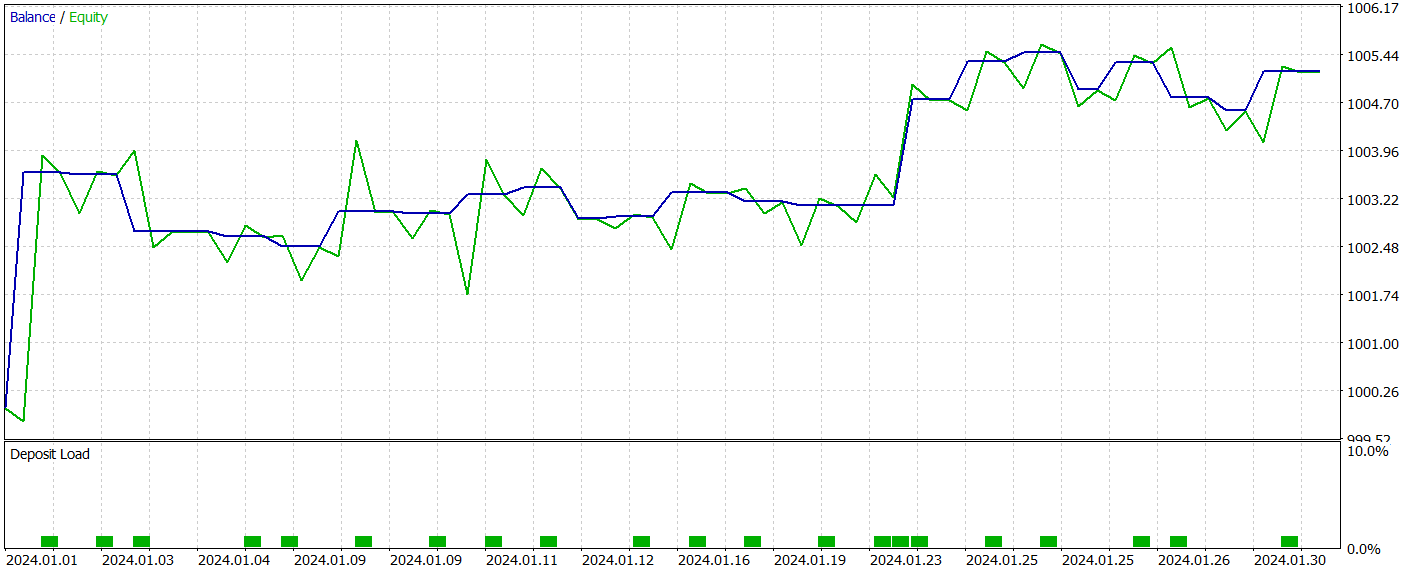
テスト期間中、モデルは22回の取引を実行し、そのうちちょうど半数が利益確定となりました。特筆すべきは、勝ちトレード1回あたりの平均利益が負けトレード1回あたりの平均損失の2倍以上であったことです。最大の利益を出した取引は最大損失の4倍を超えました。その結果、モデルのプロフィットファクターは2.63に達しました。ただし、取引回数が少なくテスト期間も短いため、本手法の長期的な有効性について決定的な結論を出すことはできません。実運用に用いる前には、より長期間の履歴データで学習させ、包括的なテストをおこなう必要があります。

結論

一般化3次元指示表現セグメンテーション(3D-GRES)法で提案されたアプローチは、市場データのより深い分析を可能にし、取引分野への有望な適用性を示しています。この手法は複数の市場シグナルをセグメント化・分析することに適応でき、複雑な市場状況をより正確に解釈し、最終的に予測精度と意思決定の向上に寄与します。

本記事の実践編では、MQL5を用いて提案手法の実装をおこないました。実験結果は、提案ソリューションが実際の取引シナリオでの利用に十分な可能性を持つことを示しています。

参照文献

記事で使用されているプログラム

#	名前	種類	詳細
1	Research.mq5	EA	事例収集のためのEA
2	ResearchRealORL.mq5	EA	Real-ORL法による事例収集のためのEA
3	Study.mq5	EA	モデル訓練EA
4	Test.mq5	EA	モデルテストEA
5	Trajectory.mqh	クラスライブラリ	システム状態記述の構造体
6	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークを作成するためのクラスのライブラリ
7	NeuroNet.cl	ライブラリ	OpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15997

添付されたファイル |

ZIPをダウンロード

MQL5.zip (1895.63 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

従来の機械学習手法を使用した為替レートの予測：ロジットモデルとプロビットモデル

この記事では、為替レートの予測を目的とした取引用EAの構築を試みます。アルゴリズムは、ロジスティック回帰およびプロビット回帰といった古典的な分類モデルに基づいています。取引シグナルのフィルターとして、尤度比検定が用いられます。

初級から中級まで：配列と文字列(III)

この記事では2つの側面について考察します。まず、標準ライブラリを使ってバイナリ値を8進数、10進数、16進数などの表現に変換する方法について説明します。次に、これまでに習得した知識を活用して、秘密のフレーズに基づいてパスワードの桁数をどのように決定できるかについて解説します。

アフリカ水牛最適化(ABO)

この記事では、アフリカ水牛の特異な行動に着想を得て2015年に開発されたメタヒューリスティック手法、アフリカ水牛最適化(ABO)アルゴリズムを紹介します。アルゴリズムの実装プロセスと、複雑な問題の解決におけるその高い効率性について詳しく解説しており、最適化分野における有用なツールであることが示されています。

リプレイシステムの開発（第68回）：正しい時間を知る(I)

今日は、流動性が低い時間帯に、マウスポインタを使ってバーの残り時間を確認できるようにする作業を引き続き進めていきます。一見すると簡単そうに思えますが、実際にはこの作業には多くの困難が伴います。いくつかの障害を乗り越える必要があるため、このサブシリーズの最初のパートをしっかりと理解しておくことが、今後の内容を理解する上で非常に重要です。