
取引におけるニューラルネットワーク:階層型ベクトルTransformer (HiVT)
はじめに
自動運転における課題は、トレーダーが直面する問題と多くの点で共通しています。動的な環境下で安全に行動を選択・実行する能力は、自動運転車にとって極めて重要です。これを実現するためには、車両が周囲の状況を正確に把握し、今後の道路上の出来事を予測できなければなりません。しかし、近くの車、自転車、歩行者などの動きを正確に予測するのは、彼らの目的や意図が明らかでない場合には特に困難です。マルチエージェントの交通シナリオにおいては、エージェントの行動は他のエージェントとの複雑な相互作用によって決定され、さらに地図に基づく交通ルールによっても左右されます。そのため、シーン内における複数エージェントの多様な行動を正確に理解・予測するのは非常に難しい課題です。
近年では、軌道データや地図要素からベクトルまたはポイントの集合を抽出するベクトル化アプローチが、よりコンパクトなシーン表現手法として注目されています。しかし、既存のベクトル化手法は、急速に変化する交通状況におけるリアルタイム予測において課題があります。これらの手法は座標系の変化に敏感であるため、一般的にターゲットエージェントを中心にし、その進行方向に合わせてシーンを正規化する処理が必要です。この手法は、予測対象となるエージェントが多数存在する場合、各エージェントごとにシーンの正規化と特徴量の再計算をおこなう必要があり、計算コストの大きなボトルネックとなります。さらに、既存手法の多くは、空間・時間両面において全要素間の関係性をモデル化しており、ベクトル化された要素間の詳細な相互作用を捉える一方で、要素数が増えるに従って計算負荷も急増します。特に自動運転の安全性を確保するためには、正確かつリアルタイムな予測が不可欠であり、この計算オーバーヘッドは深刻な課題となります。そのため、多くの研究者が、より高速かつ高精度なマルチエージェント動作予測を実現する新たなフレームワークの開発に取り組んでいます。
そのようなアプローチの1つが論文「HiVT:Hierarchical Vector Transformer for Multi-Agent Motion Prediction」で紹介されています。この方法は、対称性と階層構造を活用して、マルチエージェントの動作予測をおこないます。HiVTの著者は、動き予測タスクを複数の段階に分解し、Transformerベースのアーキテクチャを使用して要素間の相互作用を階層的にモデル化します。
最初の段階では、モデルはすべての要素間の相互作用をコスト高くモデル化することを避けるため、コンテキストの特徴を局地的に抽出します。シーン全体は、モデル化されるエージェントを中心とした一連の局地的領域に分割されます。コンテキストの特徴は、各エージェント中心の領域に存在する局地的なベクトル化要素から抽出され、中心となるエージェントに関連する豊富な情報を含みます。
第2段階では、局地的視野の制限を補い、長距離の依存関係を捉えるために、エージェント中心の領域間での大域的情報転送メカニズムが導入されます。著者は、局地的座標系間の幾何学的接続を備えたTransformerを採用し、これを実現しています。
局地的表現と大域的表現を組み合わせることで、デコーダは、モデルの単一のフォワードパスによって、すべてのエージェントの将来の軌道を予測することが可能になります。タスクの対称性をさらに活用するため、著者はすべてのベクトル化要素を相対位置で記述することで、大域的座標系のシフトに不変なシーン表現を導入します。このシーン表現に基づいて、空間学習のための回転不変なクロスアテンションモジュールが実装されており、モデルは、シーンの向きに依存することなく、局所的および大域的表現を学習可能になります。
1. HiVTアルゴリズム
HiVT法は、道路シーンをベクトル化された要素の集合として表現することから始まります。このシーン表現に基づいて、モデルは時空間情報を階層的に集約します。道路シーンはエージェントと地図情報から構成されています。構造化されたシーン表現では、まず道路エージェントの軌跡セグメントや地図データからの車線セグメントなど、ベクトル化された要素が抽出されます。
ベクトル化された要素には、意味的属性と幾何学的属性が関連付けられます。従来のベクトル化手法では、エージェントやレーンの幾何学的属性として絶対的な点の位置が含まれていますが、著者は絶対位置を避け、代わりに相対位置を用いて幾何学的属性を記述します。これにより、シーン全体がベクトルの集合として表現されます。具体的には、エージェントiの軌跡は「pt,i-pt-1,i」と表されます。ここでpt,iは時間ステップtにおけるエージェントiの位置です。
レーンセグメントxiの場合、幾何学的属性はp1,xi - p0,xiと定義されます。ここで、p0,xiとp1,xiはxiの開始座標と終了座標です。点の集合をベクトルの集合に変換することで、並進不変性が自然に保証されますが、要素間の相対位置情報が失われます。空間的関係を保持するために、エージェント間およびエージェントとレーンのペアに対して相対位置ベクトルが導入されます。たとえば、時間ステップtにおけるエージェントiに対するエージェントjの位置ベクトルはptj - ptiであり、並進不変性を保ちながらその空間的関係を完全に表現します。このシーン表現により、適用された学習関数は情報を損なうことなく並進不変性を維持できます。
高度に動的な環境でエージェントの将来の軌跡を正確に予測するには、モデルが多数のベクトル化された要素間の時空間依存関係を効果的に学習する必要があります。Transformerは、さまざまなタスクにおける要素間の長期的な依存関係を捉える能力を示しています。しかし、Transformerを時空間要素に直接適用すると、計算量はO((NT+L)^2)となります。ここで、N、T、Lはそれぞれエージェント数、履歴時間ステップ数、レーンセグメント数です。多数の要素から効率的に情報を抽出するために、HiVTは空間と時間の次元を因数分解し、各タイムステップで空間関係を局地的にモデル化します。具体的には、空間はN個の局地的領域に分割され、各局地的領域の中心にはエージェントが配置されます。各局地的領域内では、中央のエージェントの周辺環境が近隣エージェントの軌跡と局地的なレーンセグメントによって表現されます。局地的情報は各領域の特徴量ベクトルとして集約され、エージェント間相互作用、各エージェントの時間的依存関係、およびエージェントとレーンの相互作用がモデル化されます。集約された特徴量ベクトルには、中央エージェントに関する豊富な情報が含まれます。これにより、空間次元と時間次元の因数分解により計算量がO((NT+L)^2)からO(NT^2+TN^2+NL)に削減され、さらに局所領域の半径を制限することによりO(NT^2+TNk+Nl)に削減されます(ここでk < Nかつl < L)。
局所的エンコーダは豊富な表現を抽出しますが、その情報量は局地的領域によって制限されます。予測品質の低下を防ぐために、著者は、限られた局所受容野を補正し、局地的領域間のメッセージ受け渡しによってシーンレベルのダイナミクスを捉える大域的相互作用モジュールを導入しています。この大域的相互作用モジュールは、計算コストO(N^2)でモデルの表現力を大幅に向上させます。これは、局所的エンコーダに比べて比較的軽量です。
マルチエージェントの動作予測問題では、並進対称性と回転対称性が現れます。既存の方法では、各エージェントに対してすべてのベクトル化された要素を再正規化し、エージェントごとに複数の予測を行って不変性を実現します。このパラダイムはエージェントの数に応じて直線的に拡大します。対照的に、HiVTは不変シーン表現と回転堅牢な空間学習モジュールを使用することで、不変性を維持しながら、単一のフォワードパスですべてのエージェントの動きを予測できます。
エージェント間相互作用モジュールは、各時間ステップで各局地的領域内の中央エージェントと隣接エージェント間の関係をキャプチャします。問題の対称性を利用するために、著者は空間情報を集約する回転不変のクロスアテンションブロックを提案しています。具体的には、中心エージェントの最終軌道セグメントpT,i — pT-1,iを局所領域の参照ベクトルとして使用し、すべての局所ベクトルを参照方向ʘiに従って回転させます。回転したベクトルと、それに関連付けられた意味属性は、多層パーセプトロン(MLP)を使用して処理され、任意の時間ステップtにおける中心エージェントztiと任意の隣接エージェントztijの埋め込みを取得します。
すべての幾何学的属性は、MLPに入力される前に中央エージェントに対して正規化されるため、これらの埋め込みは回転不変です。入力関数фnbr(•)には、軌跡セグメントに加えて、中心エージェントに関する近傍エージェントの相対位置ベクトルも含まれており、近傍埋め込みが空間的に認識可能になります。次に、中央エージェントの埋め込みがQueryベクトルに変換され、近傍の埋め込みがKeyとValueのエンティティを計算するために使用されます。結果のエンティティはアテンションブロックで利用されます。
従来のtransformerとは異なり、hivtの著者は、環境の特徴量と中心エージェントの特徴量ztiを統合する特徴量融合関数を提案しています。これにより、アテンションブロックは特徴量の更新をより適切に制御できるようになります。元のTransformerアーキテクチャと同様に、提案されたアテンションブロックは複数のアテンションヘッドに拡張できます。マルチヘッドアテンションブロックの出力はMLPブロックに渡され、時間ステップtにおけるエージェントiの空間埋め込みstiが取得されます。
さらに、この手法の著者は、各ブロックの前に層によるデータの正規化を使用し、各ブロックの後に残差接続を使用します。実際には、このモジュールは、すべての局地的領域と時間ステップにわたる効率的な並列学習操作を使用して実装できます。
各局地的領域の時間情報のさらなるキャプチャは、エージェント間相互作用モジュールに続く時間的Transformerエンコーダを使用して実装されます。任意の中央エージェントiについて、このモジュールの初期シーケンスは、異なる時間ステップでエージェント間相互作用モジュールから受信した埋め込みstiで構成されます。この手法の作者は、元のシーケンスの末尾に、追加の訓練可能なトークンsT+1を追加します。次に、学習可能な位置エンコーディングをすべてのトークンに追加し、トークンを行列Siに配置して時間的アテンションブロックに入力します。
時間的学習モジュールは、マルチヘッドアテンションブロックとMLPブロックが交互に積み重ねられることで構成されます。
地図の局地的構造は、中央エージェントの将来の意図を示す可能性があります。したがって、中央エージェントの埋め込みに局地的地図情報が追加されます。この処理では、まず局地的道路セグメントと、現在の時間ステップTにおける道路エージェントの相対位置ベクトルを回転させます。回転後のベクトルは、MLPを使用して符号化されます。その後、中央エージェントの時空間特徴量をqueryとして、MLPで符号化された道路セグメントの特徴量をKey-Valueベクトルとして使用し、上述のアプローチと同様に、エージェントと道路の交差アテンション機構(クロスアテンション)を実現します。
この手法の著者は、中心エージェントiの最終的な局地的埋め込みhiを取得するために、さらにMLPブロックを適用します。エージェント間の相互作用、時間的な依存性、エージェントと道路の相互作用を順番にモデル化した後、埋め込みは局地的領域の中央エージェントに関連する豊富な情報をカプセル化します。
HiVTアルゴリズムの次の段階では、局所的な埋め込みが大域的相互作用モジュールで処理され、シーン内の長距離依存関係を捉えます。局所的な特徴はエージェント中心の座標系で抽出されるため、大域的相互作用モジュールでは、異なる座標フレーム間の幾何学的関係を考慮しながら、局所領域間で情報をやり取りする必要があります。この目的のため、著者はTransformerエンコーダを拡張し、局所座標系間の差異を取り入れました。エージェントjからエージェントiに情報を送る際には、MLPによってペアワイズな埋め込みを生成し、それをベクトル変換に組み込みます。
ペアワイズな大域的相互作用をモデル化するために、局所エンコーダで用いられた空間的アテンションメカニズムを同様に適用し、続いて各エージェントの大域的表現を出力するMLPブロックを通します。
交通エージェントの将来の動きは本質的にマルチモーダルであるため、著者は、各成分がラプラス分布に従う混合モデルとして、将来軌道の分布をパラメータ化することを提案しています。予測は、すべてのエージェントに対して単一のフォワードパスで生成されます。各混合成分fに対して、各エージェントiについて、MLPは局所表現と大域的表現を入力として受け取り、局所座標系における将来の各時間ステップにおけるエージェントの位置と、それに伴う不確実性を出力します。回帰ヘッドの出力テンソルは[F、N、H、4]の次元を持ちます。ここで、Fは混合成分数、Nはシーン内のエージェント数、Hは将来の予測ステップ数です。ここでもMLPが用いられ、続いてSoftmaxにより、各エージェントの混合モデルに対する係数が決定されます。
著者によるHiVT法の視覚化を以下に示します。

2. MQL5での実装
HiVTの著者によって提案された包括的なアルゴリズムを確認しました。ここからは、これらの手法に対する私たちの解釈を基に、MQL5を用いた実装の実務的な側面に移ります。
なお、HiVT著者が提案するアプローチは、これまで私たちが用いてきた手法とは大きく異なる点に注意が必要です。そのため、今後取り組む作業は相当な規模になることが予想されます。
2.1 初期状態のベクトル化
まず、状態ベクトル化のプロセスを整理することから始めます。これまでに私たちは、区分的線形時系列表現、データのセグメンテーション、さまざまな埋め込み技術など、複数の状態ベクトル化アルゴリズムを検討してきました。しかし今回、著者はこれまでとは根本的に異なる手法を提案しています。この手法は、HiVTPrepareカーネルのOpenCL側に実装していきます。
__kernel void HiVTPrepare(__global const float *data, __global float2 *output ) { const size_t t = get_global_id(0); const size_t v = get_global_id(1); const size_t total_v = get_global_size(1);
カーネルのパラメータとしては、グローバルメモリ上のデータバッファへのポインタを2つのみ使用します。1つは入力値用、もう1つは演算結果用です。
ここで重要なのは、入力データとは異なり、結果バッファにはfloat2型のベクトルを使用している点です。以前はこの型を複素数の表現に用いていましたが、今回は複素数演算はおこないません。このデータ型の採用は、2次元空間におけるシーンの回転を処理する必要性によるものであり、2要素のベクトルを使用することで、平面上の座標と変位を効率的に格納することができます。
ご覧の通り、カーネルパラメータには、入力テンソルおよび出力テンソルの次元を定義する定数は明示的に含まれていません。これらの情報は、2次元のタスク空間から導出する設計としています。第1次元は解析対象となる履歴の深さを示し、第2次元は処理対象のマルチモーダル系列内に含まれる単変量時系列の数を表します。
この方法は、マルチモーダル系列が1次元の単変量時系列の集合として構成されているという前提に基づいています。
カーネル本体では、タスク空間の各次元にわたって現在のスレッドを識別し、それに基づいてグローバルデータバッファ内で使用するオフセット定数を算出します。
const int shift_data = t * total_v; const int shift_out = shift_data * total_v;
結果バッファのオフセットを明確にするために、このカーネルで実装を予定しているアルゴリズムについて少し補足しておきます。
理論パートでも触れたように、HiVT手法の著者は、中心エージェントを基準としたシーン全体の回転により、絶対座標を相対座標に置き換えるというアプローチを提案しています。
この考え方に従い、まずは各エージェントのバイアス(相対的な位置のズレ)を、ある特定の時間ステップにおいて算出します。
float value = data[shift_data + v + total_v] - data[shift_data + v];
次に、得られた変位の傾斜角を計算します。平面上で傾斜角を求めるには本来2つの変位座標が必要ですが、入力データには1つの値しか含まれていません。とはいえ、これは時系列データであるため、時間軸に沿った単位ステップを仮定することで、もう1つの座標を導き出すことができます。つまり、時間軸方向の変位を「1」と仮定することで、2次元空間上での傾きを計算可能になります。
const float theta = atan(value);
これで、角度の正弦と余弦を決定して回転行列を構築できます。
const float cos_theta = cos(theta); const float sin_theta = sin(theta);
その後、中心エージェントの移動ベクトルを回転させることができます。
const float2 main = Rotate(value, cos_theta, sin_theta);
すべてのエージェントに対して回転処理をおこなう必要があるため、この操作は別関数として切り出しました。
回転を適用すると、2つの座標軸に沿った変位が得られる点に注意が必要です。このデータを格納するために、ベクトル型変数float2を使用します。
続いて、特定の時間ステップに存在するすべてのエージェントを対象にループ処理を実行します。
for(int a = 0; a < total_v; a++) { float2 o = main; if(a != v) o -= Rotate(data[shift_data + a + total_v] - data[shift_data + a], cos_theta, sin_theta); output[shift_out + a] = o; } }
中央エージェントのループ本体では、そのエージェント自身の動きを保存し、その他のエージェントについては中央エージェントに対する相対的な動きを計算します。この処理では、まず各エージェントの位置のシフトを算出し、それを中央エージェントの回転行列に従って回転させます。その後、得られた変位から中央エージェントの動きベクトルを差し引くことで、相対的な動きを求めます。
このようにして、各エージェントの各タイムステップにおいて、2列(平面上の座標)を持ち、行数が解析対象となる一変量系列の数に等しいシーン記述テンソルを得ることができます。
ここで補足しておくべき点として、本手法の著者はエージェントの数を局所セグメントの半径によって制限していました。一方で、ここではこの制限を設けていません。というのも、指標値の乖離が有用なトレードシグナルとなることが多いためです。
2.2 単一時間ステップ内のアテンション
提案されたアプローチを実装する中で次に直面した課題は、同一の時間ステップ内におけるエージェント間のアテンションメカニズムの構築でした。
これまで私たちは、個々の変数(時系列)内でアテンションメカニズムを実装しており、これは「垂直方向」の分析に該当します。しかし今回必要となるのは、「水平方向」の分析です。もちろん、新たに「水平アテンション」クラスを作成して対応することも可能ですが、これはかなり手間のかかる方法です。
より迅速な解決策として、元のデータを転置し、既存の「垂直アテンション」処理を流用するという手があります。ただし、ここにはひとつ注意点があります。従来の2次元行列転置アルゴリズムはこのケースには適していません。そのため、今回は3次元テンソルを転置する専用のアルゴリズムを新たに構築します。具体的には、テンソルの第1次元と第2次元を入れ替え、第3次元はそのまま保持します。
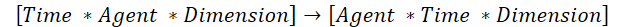
これはまさに、既存の「垂直アテンション」アルゴリズムを活用するために必要なステップです。
この処理を体系的におこなうために、TransposeRCDカーネルを新たに作成します。
__kernel void TransposeRCD(__global const float *matrix_in, ///<[in] Input matrix __global float *matrix_out ///<[out] Output matrix ) { const int r = get_global_id(0); const int c = get_global_id(1); const int d = get_global_id(2); const int rows = get_global_size(0); const int cols = get_global_size(1); const int dimension = get_global_size(2); //--- matrix_out[(c * rows + r)*dimension + d] = matrix_in[(r * cols + c) * dimension + d]; }
カーネルアルゴリズムは、2次元行列の転置に対する同様のカーネルをほぼ完全に繰り返していると言えます。ただし、タスクスペースの次元が1つ追加されるため、それに伴いデータバッファ内のオフセットも調整されます。
CNeuronTransposeRCDOCLクラスの構造についても同様のことが言えます。ここでは、2D行列転置クラスCNeuronTransposeOCLを親として使用します。
class CNeuronTransposeRCDOCL : public CNeuronTransposeOCL { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronTransposeRCDOCL(void){}; ~CNeuronTransposeRCDOCL(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint count, uint window, uint dimension, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronTransposeRCDOCL; } };
クラス本体では、追加の変数やオブジェクトを宣言しない点に注意してください。プロセスの実装には、継承したメソッドで十分です。このため、カーネル呼び出しメソッドのみをオーバーライドすることができ、その他の機能は親クラスのメソッドでカバーされています。したがって、クラスメソッドのアルゴリズムについては詳しく説明しません。ご自身で確認することをお勧めします。このクラスとそのすべてのメソッドの完全なコードは添付ファイルに含まれています。
2.3 エージェント間アテンションブロック
次に、エージェント間アテンションブロックの実装に移ります。このブロックのフレームワークでは、1つの時間ステップ内でエージェントの局地的埋め込み同士でアテンションが構築されることを想定しています。前述の3次元テンソル転置クラスのおかげで、作業は大幅に簡素化されました。しかし、著者が提案した特徴量統合制御機構を使用するためには、アルゴリズムの調整が必要です。
この指定されたアテンションブロックのプロセスを整理するために、新しいクラスCNeuronHiVTAAEncoderを作成します。この場合、独立変数アテンション層であるCNeuronMVMHAttentionMLKVを親クラスとして使用します。
class CNeuronHiVTAAEncoder : public CNeuronMVMHAttentionMLKV { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronHiVTAAEncoder(void){}; ~CNeuronHiVTAAEncoder(void){}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronMVMHAttentionMLKV; } };
ご覧の通り、このクラスの構造では追加の変数やオブジェクトを宣言していません。親クラスの構造が十分に対応しています。CNeuronMVMHAttentionMLKVクラスは、データバッファの動的コレクションを使用しており、これらのデータバッファはクラスのメソッドで操作されます。また、必要に応じて、既存のコレクションにデータバッファを追加することができます。
クラスオブジェクトの新しいインスタンスの初期化はInitメソッドで実装されます。
bool CNeuronHiVTAAEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint heads_kv, uint units_count, uint layers, uint layers_to_one_kv, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count * variables, optimization_type, batch)) return false;
メソッドパラメータでは、ユーザーが指定したオブジェクトのアーキテクチャを正確に判別できるようにする主要な定数を受け取ります。メソッドの本体では、ニューラル層基底クラスの同じメソッドを呼び出します。
直接の親ではなく、基底クラスのメソッドを呼び出していることに注意してください。これは、後でいくつかのデータバッファを再定義する必要があるためです。
親クラスメソッドが正常に実行された後、外部プログラムから受信したオブジェクトアーキテクチャ定義の定数を内部変数に保存します。
iWindow = fmax(window, 1); iWindowKey = fmax(window_key, 1); iUnits = fmax(units_count, 1); iHeads = fmax(heads, 1); iLayers = fmax(layers, 1); iHeadsKV = fmax(heads_kv, 1); iLayersToOneKV = fmax(layers_to_one_kv, 1); iVariables = variables;
次に、内部オブジェクトのサイズを決定する定数をすぐに計算します。
uint num_q = iWindowKey * iHeads * iUnits * iVariables; //Size of Q tensor uint num_kv = iWindowKey * iHeadsKV * iUnits * iVariables; //Size of KV tensor uint q_weights = (iWindow * iHeads + 1) * iWindowKey; //Size of weights' matrix of Q tenzor uint kv_weights = (iWindow * iHeadsKV + 1) * iWindowKey; //Size of weights' matrix of KV tenzor uint scores = iUnits * iUnits * iHeads * iVariables; //Size of Score tensor uint mh_out = iWindowKey * iHeads * iUnits * iVariables; //Size of multi-heads self-attention uint out = iWindow * iUnits * iVariables; //Size of attention out tensore uint w0 = (iWindowKey * iHeads + 1) * iWindow; //Size W0 weights matrix uint gate = (2 * iWindow + 1) * iWindow; //Size of weights' matrix gate layer uint self = (iWindow + 1) * iWindow; //Size of weights' matrix self layer
アルゴリズムは基本的に親クラスから継承されており、いくつかの小さな編集のみが加えられています。
準備作業が完了したら、指定されたネストされた層の数に等しい反復回数のループを作成します。このループの本体では、各反復で、個々のネストされた層の機能を実行するために必要なオブジェクトを作成します。
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL; for(int d = 0; d < 2; d++) { //--- Initilize Q tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_q, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
ここではまず、中間データおよび各ブロックの結果を保存するためのバッファを作成し、それに対応する誤差勾配を記録するバッファも作成します。
データバッファと対応する誤差勾配のバッファは同じサイズになるため、手作業を減らす目的で、2回の反復を行うネストされたループを用意します。最初の反復ではデータバッファを、2回目の反復ではその誤差勾配バッファを生成します。
まずはQueryエンティティを書き込むためのバッファを作成し、続いてKeyおよびValue用のバッファを作成します。
//--- Initilize KV tensor if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Tensors.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(2 * num_kv, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!KV_Tensors.Add(temp)) return false; }
データバッファを作成および初期化するアルゴリズムは完全に同一です。唯一の違いは、私たちのアルゴリズムでは、複数のネストされた層に対して1つのKey-Valueテンソルを使用できることです。したがって、バッファを作成する前に、現在の層でこのアクションの必要性を確認します。
次に、オブジェクト間の依存係数のバッファを初期化します。
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
そして、マルチヘッドアテンション出力バッファも初期化します。
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
マルチヘッドセルフアテンションアルゴリズムに従って、マルチヘッドアテンションの結果は、投影層を使用して元のデータレベルに圧縮されます。結果の投影を保存するためのバッファを作成します。
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
ここまでに説明したアルゴリズムは、親クラスのメソッドをほぼ完全に繰り返します。しかし、さらに先では、特徴量の統合を管理するためのメカニズムを実装するために変更が導入されました。ここで、提案されたアルゴリズムによれば、最初にソースデータとアテンションブロックの結果を連結する必要があります。
//--- Initialize Concatenate temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(2 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
その結果は制御係数を計算するために使用されます。
//--- Initialize Gate temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
その後、元のデータの投影をおこないます。
//--- Initialize Self temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
ネストされたループの最後に、現在のネストされた層の出力バッファを作成します。
//--- Initialize Out if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
ここで注目すべき点は、出力および誤差勾配のバッファは中間の内部レイヤーに対してのみ作成するということです。最も内側の層については、単にクラス内の対応するバッファへのポインタをコピーするだけです。
中間結果のバッファと対応する誤差勾配バッファを作成した後は、学習用パラメータ行列の初期化をおこないます。これらの行列はいくつか存在します。まずは、Queryエンティティを生成するための行列です。
//--- Initilize Q weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(q_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < q_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
ここでは、まずバッファを作成し、それをランダムなパラメータで埋めます。これらのパラメータは、モデルの訓練プロセス中に最適化されます。
同様に、KeyとValueエンティティ生成用のパラメータも作成します。ただし、ネストされた層ごとに行列を生成するわけではありません。
//--- Initialize K weights if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(kv_weights)) return false; for(uint w = 0; w < kv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; }
さらに、マルチヘッドアテンションの結果の投影行列が必要になります。
//--- Initialize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
ここで、特徴量の組み合わせ制御ブロックのパラメータも追加します。
//--- Initialize Gate Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(gate)) return false; k = (float)(1 / sqrt(2 * iWindow + 1)); for(uint w = 0; w < gate; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
そして、ソースデータの予測も追加します。
//--- Self temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(self)) return false; k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < self; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
次に、パラメータの最適化プロセスで使用される、重み行列に対するモーメンタム値を保存するためのデータバッファを追加する必要があります。
//--- for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? q_weights : iWindowKey * iHeads), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; if(i % iLayersToOneKV == 0) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!K_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? kv_weights : iWindowKey * iHeadsKV), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!V_Weights.Add(temp)) return false; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? w0 : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize Gate Momentum temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? gate : 2 * iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize Self Momentum temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit((d == 0 || optimization == ADAM ? self : iWindow), 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } }
ネストされた層オブジェクトの初期化が正常に完了したら、中間結果を一時的に記録するために使用される追加のバッファを作成します。
if(!Temp.BufferInit(MathMax(2 * num_kv, out), 0)) return false; if(!Temp.BufferCreate(OpenCL)) return false; //--- return true; }
メソッドの実行を完了します。その後、メソッド操作のブール結果を呼び出し元プログラムに返します。
オブジェクトを初期化した後の次のステップは、feedForwardメソッドで実装されるフィードフォワードパスアルゴリズムを構築することです。
bool CNeuronHiVTAAEncoder::feedForward(CNeuronBaseOCL *NeuronOCL) { if(CheckPointer(NeuronOCL) == POINTER_INVALID) return false;
このメソッドのパラメータでは、初期データを持つオブジェクトへのポインタを受け取り、受け取ったポインタの関連性をすぐに確認します。この制御が正常に完了すると、それぞれのネストされた層の操作を順番に実行するループを実行します。
CBufferFloat *kv = NULL; for(uint i = 0; (i < iLayers && !IsStopped()); i++) { //--- Calculate Queries, Keys, Values CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(10 * i - 6)); CBufferFloat *q = QKV_Tensors.At(i * 2); if(IsStopped() || !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, iWindow, iWindowKey * iHeads, None)) return false;
まず、Queryエンティティを生成します。次に、必要に応じて、Key-Valueテンソルを形成します。
if((i % iLayersToOneKV) == 0) { uint i_kv = i / iLayersToOneKV; kv = KV_Tensors.At(i_kv * 2); CBufferFloat *k = K_Tensors.At(i_kv * 2); CBufferFloat *v = V_Tensors.At(i_kv * 2); if(IsStopped() || !ConvolutionForward(K_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, k, iWindow, iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !ConvolutionForward(V_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, v, iWindow, iWindowKey * iHeadsKV, None)) return false; if(IsStopped() || !Concat(k, v, kv, iWindowKey * iHeadsKV * iVariables, iWindowKey * iHeadsKV * iVariables, iUnits)) return false; }
必要なエンティティのテンソルを形成した後、マルチヘッドアテンションの結果を計算できます。
//--- Score calculation and Multi-heads attention calculation CBufferFloat *temp = S_Tensors.At(i * 2); CBufferFloat *out = AO_Tensors.At(i * 2); if(IsStopped() || !AttentionOut(q, kv, temp, out)) return false;
次に、それらを初期データの次元に圧縮します。
//--- Attention out calculation temp = FF_Tensors.At(i * 10); if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, iWindowKey * iHeads, iWindow, None)) return false;
制御係数を計算するには、まずアテンションブロックの結果と初期データを連結します。
//--- Concat out = FF_Tensors.At(i * 10 + 1); if(IsStopped() || !Concat(temp, inputs, out, iWindow, iWindow, iUnits)) return false;
次に制御係数を計算します。
//--- Gate if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), out, FF_Tensors.At(i * 10 + 2), 2 * iWindow, iWindow, SIGMOID)) return false;
次に、元の入力の投影をおこなう必要があります。
//--- Self if(IsStopped() || !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), inputs, FF_Tensors.At(i * 10 + 3), iWindow, iWindow, None)) return false;
その後、制御係数を考慮して、得られた投影とアテンションブロックの結果を組み合わせます。
//--- Out if(IsStopped() || !GateElementMult(FF_Tensors.At(i * 10 + 3), temp, FF_Tensors.At(i * 10 + 2), FF_Tensors.At(i * 10 + 4))) return false; } //--- return true; }
その後、サイクルの新しい反復で次のネストされた層の作業に進みます。
ブロック内のすべてのネストされた層の操作が正常に完了したら、メソッドの実行を終了し、操作の完了ステータスを示す論理結果を呼び出し元に返します。
フィードフォワードアルゴリズムの実装に関する研究はこれで完了しました。バックプロパゲーション法のアルゴリズムを独自に理解しておくことをお勧めします。この記事の作成に使用したすべてのプログラムと同様に、すべてのクラスとそのメソッドの完全なコードは添付ファイルにあります。
結論
本稿では、複数のエージェントの動きを予測するために提案された、非常に興味深く将来性のある手法である階層型ベクトルTransformer (HiVT)について検討しました。この手法は、予測問題を局所的なコンテキスト抽出と大域的な相互作用モデリングのステージに分解することで、効果的なアプローチを提供します。
HiVTの提案者たちは、課題解決に対して包括的なアプローチを取り、モデルの有効性を高めるためのいくつかの技術的工夫を導入しました。残念ながら、それらの実装に必要な作業量はこの記事の枠を超えているため、本稿では準備段階の内容にとどめました。開始された作業は次回の記事で完了する予定であり、提案手法を実際の履歴データに対してテストした結果も次回にて報告します。
参照文献
記事で使用されているプログラム
| # | ファイル名 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | StudyEncoder.mq5 | EA | エンコーダ訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/15688
 多通貨エキスパートアドバイザーの開発(第17回):実際の取引に向けたさらなる準備
多通貨エキスパートアドバイザーの開発(第17回):実際の取引に向けたさらなる準備
 初級から中級へ:WHILE文とDO WHILE文
初級から中級へ:WHILE文とDO WHILE文
 MQL5でパラボリックSARと単純移動平均(SMA)を使用した高速取引戦略アルゴリズムを実装する
MQL5でパラボリックSARと単純移動平均(SMA)を使用した高速取引戦略アルゴリズムを実装する
 取引におけるニューラルネットワーク:統合軌道生成モデル(UniTraj)
取引におけるニューラルネットワーク:統合軌道生成モデル(UniTraj)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索